钢筋混凝土开口剪力墙平面外受力性能弹性数值分析

邓良号,曹 朗,曹帧记,袁海俊

(河海大学 土木与交通学院,江苏 南京 210098)

钢筋混凝土开口剪力墙平面外受力性能弹性数值分析

邓良号,曹 朗,曹帧记,袁海俊

(河海大学 土木与交通学院,江苏 南京 210098)

运用有限元软件ANSYS对多组开口剪力墙试件计算分析,在此基础上得到:墙肢内力除应按一维压弯构件进行计算外,还应在“有效宽度”范围内叠加连梁荷载的内力效应,并提出了墙肢内力可按一维压弯构件计算的尺寸条件及“有效宽度”的近似计算方法。

开口混凝土剪力墙;平面外受力;挠度和内力近似解;一维压弯构件;变形等效

文献[1-3]基于弹性薄板理论分别对非开口情况下的钢筋混凝土剪力墙进行受力性能研究,在理论分析的基础上把剪力墙的最不利内力和一维压弯构件的内力进行比较,提出实际工程中偏于安全地一维压弯构件计算剪力墙平面最大弯矩的近似计算方法。鉴于开口剪力墙理论分析有一定难度,本文用有限元程序ANSYS分析多组开口剪力墙,得到了墙肢平面外弯矩和挠度的分布规律,并为工程设计提出了内力近似分析方法及配筋建议。

1 基本模型

对于开口剪力墙,从理论上很难求解出剪力墙上下端的荷载,本文取沿墙边最大弯矩M1和竖向力Nx均匀作用在墙体上下端(如图1),较实际情况偏于安全。为便于研究,本文取模型洞口位于墙体中央,即左右墙肢宽度相等,上下连梁的高度相等由于剪力墙受到楼板在水平方向的约束作用,剪力墙上下两端的约束条件简化为铰支;剪力墙侧端还受到相邻纵墙的约束作用,偏安全考虑,本文假定相连纵墙对剪力墙的约束为简支。

图1 基本模型

在图1基本模型中,对于连梁,荷载直接施加在其上,由于墙肢对其两端约束较大,可近似简化为固支,可用静力平衡的方法求出连梁端截面内的扭矩,并按弯扭构件对连梁进行结构设计。而墙肢的受力情况较为复杂,下文主要对墙肢的受力情况进行研究。

2 基本模型分解

根据叠加原理,将基本模型分解为分别受荷载S1、荷载S2作用的分解模型进行研究,如图2(a)～2(c)所示。下文将运用有限元软件ANSYS对两种荷载单独作用下的墙肢内力和挠度进行研究。

图2 基本模型及分解模型

3 墙肢在荷载S1作用下受力性能研究

3.1 采用近似方法的依据

图3(a)为一维压弯扁柱,其弯矩Mx和挠度可以通过材料力学按一维压弯构件计算得到。图3(b)为基本模型,相对于3(a),构件右端多了连梁的约束作用,左端多了简支边,因此3(b)构件的弯矩和挠度应较3(a)小,但当墙肢宽高比足够大、连梁高度较小时,墙肢中间大部分区域的弯矩Mx和挠度接近一维压弯构件的弯矩和挠度,仅在左右两侧较小范围内大幅减小。本文拟用一维压弯构件来模拟墙肢的弯矩Mx和挠度,且在构件两侧边偏于安全。

3.2 墙肢平面外弯矩Mx和挠度沿y方向分布情况研究

本文研究了连梁高度、连梁跨度、墙肢宽度、层高对墙肢平面外弯矩Mx和挠度沿y方向分布的影响。所选用试件尺寸如表1所示,墙肢上下端竖向力Nx=300 kN/m,弯矩M1=30 kN◦m/m,混凝土强度等级为 C30,泊松比为0.2,弹性模量为30 kN/mm2。利用ANSYS建立模型,采用8节点solid45单元模拟剪力墙并进行弹性分析[4]。分析试件在S1荷载作用下的墙肢沿y方向的Mx和挠度分布情况。

图3 采用近似方法的依据

表1 试件尺寸

由于墙肢关于y轴成反对称,取墙肢上半部分进行分析研究即可反映整块墙肢的内力情况。取连梁高度范围中线、上半洞口高度范围中线上的数据制图,以反映连梁高度范围内和上半洞口高度范围内Mx和挠度沿y轴的分布情况,如图4所示,其中hole表示上半洞口高度中线数据,beam表示连梁高度中线处的数据。

为了便于研究,定义:

其中:hb为连梁高度;H为层高度;W为墙肢宽度;lb为连梁的跨度。

图4 所取数据位置

通过对计算结果分析得到如下结论:

(1)当k3＞1时,连梁跨度的改变对墙肢弯矩Mx和挠度没有影响,因此不考虑连梁跨度对本文问题的影响。

(2)结合3.1节的结论知:在连梁高度范围内,弯矩Mx和挠度在沿y方向的中间区域内分布较为平缓,其值接近于与其相同尺寸的一维压弯构件;在上半洞口高度范围的右侧区域内弯矩Mx和挠度分布较为平缓,其值接近于与其相同尺寸的一维压弯构件,且k1越小、k2越大时上述现象越明显。因此,可以取平缓区域内的最大值作为该区域的代表值和一维压弯构件内力和弯矩进行并比较,以反映本文所提近似方法的精确度。

在连梁高度范围内,平缓区域内Mx和挠度沿y方向峰值集中在0.5W～0.7W之间,当k2＞2/3时,可以近似地认为y=0.6W为Mx和挠度沿y方向峰值的y坐标;在上半洞口高度范围内的平缓区域Mx和挠度沿y方向峰值都处于洞口边,即y=W边。考虑弯矩在洞口角点区域的弯矩突变,对于Mx,取y=0.9W和y=0.6W作为墙肢弯矩Mx沿y方向最大值的位置,而挠度取y=W和y=0.6W作为墙肢挠度沿y方向的最大值位置。

3.3 近似方法影响的因素及适用范围

由3.2节可知,连梁跨度对墙肢内力没影响,仅研究k1、k2对近似方法精确度的影响。基于ANSYS有限元程序,计算试件J1～J4、J9～J12在S1荷载作用下的平面外弯矩Mx最大值和挠度最大值。

k1较小,近似解的误差较小,k1增加,近似解的误差增大,当k1=4/15时,Mx和挠度的误差都接近10%。

在k1不变的情况下,k2增加,近似解的误差减小,k2接近于2.5/3时,挠度的误差已经达到10%,k2接近于2/3时,弯矩的误差接近10%。

从上面的分析可知,在S1单独作用下的近似方法适用于k1较小而k2较大的情况,为给工程实践提供参考依据,将近似解误差在10%之内的墙肢尺寸条件制表,如表2。

表2 近似方法的适用范围

4 墙肢在荷载S2外力作用下受力性能研究

4.1 等效模型的确定

Kwan[5]在研究梁-墙平面外节点时,提出用“等效计算模型”代替之的方法,除与连梁相连的一侧外,另外三侧皆为铰支,如图5(a)所示。图5(b)中,由于墙体在连梁截面范围内的平面外刚度很大,假设连梁高度范围的虚柱刚度无限大,等效为刚域,如图5(c),并假设连梁传递给墙肢的荷载完全由虚柱承担,且在连梁的高度范围内成线性关系,即q=3M1/hb2。

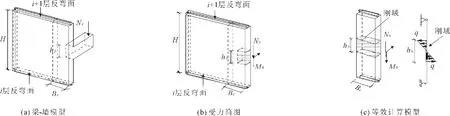
图5 Kwan的模型分析

基于相同荷载作用下“梁-墙模型”中梁高中点处的转角等于“等效计算模型”中梁高中点处转角的“变形等效”原则确定虚柱宽,即“等效宽度”,如图5c所示。

本文在多层基本模型的基础上取上下两层墙体的反弯面间的墙体进行研究,并考虑楼板的平面外方向的约束作用,如图6(a)。在基本模型中,楼板仅对墙肢平面外方向有约束作用,图6(a)的墙体关于楼板约束位置上下成反对称,故楼板对墙体约束作用很小,可以忽略不计,因此,本文“梁-墙模型”的受力简图和Kwan的受力简图是相同的,如图6(b)所示。依照 Kwan的方法,可采用图 6(c)的“等效计算模型”代替图6(a)的“梁-墙模型”。

图6 本文模型分析

本文拟采用“墙-梁模型”洞口边缘反弯点b转角θb与“等效计算模型”B点转角θB相等的“变形等效”原则确定“等效宽度”Bc,由于“等效计算模型”为反对称结构,仅取该模型下半部分(基本模型的上半部分)进行分析,并由材料力学[5]知,B点的转角公式为:

由变形等效原则 θB=θb,可得

因此,只要确定反弯点处的转角,就可确定有效宽度的大小。

4.2 数值分析及有效宽度公式拟合

下文在大量试件分析的基础上确定有效宽度影响因素并给出有效宽度的简单求解公式。所取试件的层高H=3 m,墙厚h=250 mm,梁跨度lb=2.7 m,墙肢宽W及梁高hb的尺寸如表3,仅受S2作用,其余参数同3.2节,用ANSYS对试件分析,求解角度θb,如表3。通过公式(5)可求解出表3中试件对应的有效宽度,如表4。

用ANSYS分析表5中试件,并求解角度θb,如表5,表中试件的墙肢宽度W=3 m,连梁高度hb=0.6 m,梁跨度lb=2.7 m,仅受S2作用,其余参数同3.2节。通过公式(5)可求解出表5中试件对应的有效宽度,如表6。

表3 不同墙宽和梁高条件下θb 单位:10-4rad

表4 不同墙宽和梁高条件下有效宽度 单位:mm

表5 不同墙厚和层高条件下θb 单位:10-4rad

表6 不同墙厚和层高条件下有效宽度 单位:mm

由表3和表4可知:当k2大于0.5时,墙肢宽度对有效宽度没有影响,对于实际工程,一般都可以满足该条件;当梁高大于墙厚时,梁高对有效宽度的影响可以忽略不计。由表5和表6数据可知,墙厚和层高与有效宽度成正比关系,根据origin8.0对表5、表6数据进行拟合,可以得有效宽度的求解公式为:

式中:Bc表示有效宽度;H表示层高;h表示墙厚。因此,当k2大于0.5时,可用式(6)求解Bc。

5 实例分析

由第2节知,基本模型可由分解模型1和分解模型2叠加得到的,将分解模型1和分解模型2的近似方法解叠加即可得到本文基本模型的近似解,并将最不利内力结果作为结构设计的依据。取J1试件来说明基本模型近似解的求解过程。

试件尺寸满足表2的要求,因此可以用分解模型1的近似方法来求解S1单独作用下墙肢的内力解,由材料力学求解一维压弯构件内力作为墙肢的平面外弯矩和挠度[5]:

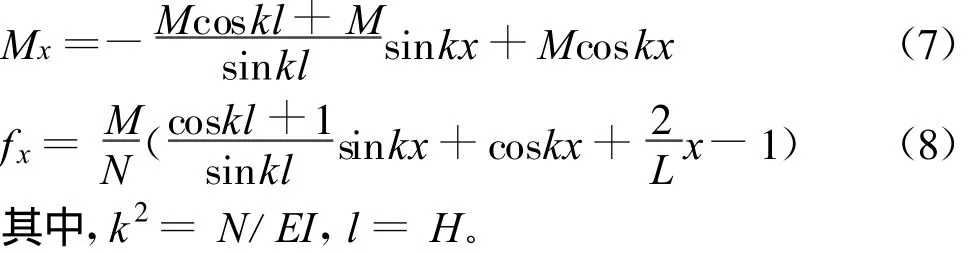
又知k2大于0.5,则可由式(5)得Bc=852 mm,根据材料力学,图6(c)等效计算模型下半部分对应的弯矩和挠度公式如下[6]:连梁高度范围内:洞口高度范围内:

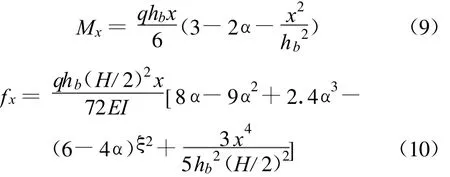
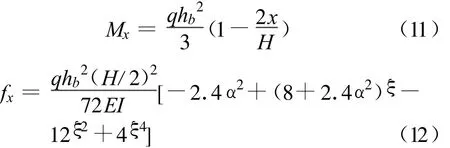
在有效宽度以外,墙肢内力就是分解模型1的近似解,Mxmax=30 000 kN◦m/m;而在有效宽度内,墙肢内力由分解模型1近似解、分解模型2近似解叠加而得,Mxmax=57 967 kN◦m/m。最大值乘上分项系数作为竖向配筋计算的设计值[7]。

6 小 结

(1)当开口剪力墙的尺寸同时满足表2和k2＞0.5的条件时,其内力和挠度可采用近似的方法进行求解:在靠近洞口一侧可采用分解模型1、2的近似方法结果叠加得到;而另外一侧可直接采用分解模型1的近似进行承载力设计。

(2)本文提出的近似解法主要为结构设计提供内力依据,只能近似地反映出墙肢内力的分布情况,因此本文解与实际内力情况仍存在一定误差,但对对称剪力墙基本能满足工程设计的精确要求。

(3)本文提出的两种近似方法都是在墙肢侧为铰支的前提下提出的,而相连墙体对墙肢的约束作用要强于铰支约束,因此本文解偏于安全。

[1]邵旭斌.大空间住宅剪力墙出平面承载力研究[D].南京:河海大学,2005.

[2]张海滨.大空间住宅钢筋混凝土剪力墙出平面受力分析及配筋计算[D].南京:河海大学,2008.

[3]刘少刚.大空间小高层剪力墙结构的受力分析[D].南京:河海大学,2007.

[4]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2011.

[5]Kwan A K H,ChanW T.Non-planar beam wall joints in tall building structures[J].Structures&Buildings,2000,140(1):73-83.

[6]孙训方,方孝淑.材料力学(第四版)[M].北京:高等教育出版社,2001.

[7]陈 丹.钢筋混凝土梁墙节点平面外受力性能研究[D].北京:北京交通大学,2006.

Elastic Numerical Analysis on Out-of-plane Forcing Behavior of Reinforced Open Concrete Shear-wall

DENG Liang-hao,CAO Lang,CAO Zhen-ji,YUAN Hai-jun
(College of Civil and Traffic Engineering,Hohai University,Nanjing,Jiangsu210098,China)

Using the finite element software ANSYS,many groups of open shear-wall are calculated and analyzed,and based on this,the conclusion is obtained that the internal force of wall limb should be calculated as one dimensional press-bending member,and the internal force of beam loadsshould be added to the limb in“effective width” .Simultaneously,the size conditions that the limb could be reinforced as press-bending member and the approximate calculation method of“effective width” are put forward.

open concrete shear-wall;out-of-plane forcing;approximate solution of deflection and internal force;one dimensional press-bending member;equivalent deformation

TU375

A

1672—1144(2013)02—0146—05

2012-11-09

2012-12-19

邓良号(1987—),男,江苏宿迁人,硕士研究生,研究方向为新型结构与钢-混凝土组合结构性能与设计。