E＝mc2，我的所爱

丁庆红 冯 爽

（1.北京教育学院石景山分院，北京 100043；2.北京教育学院教师教育数理学院，北京 100044）

《E＝mc2，我的所爱》（E＝mc2，mon amour）是科万（Patrick Cauvin）撰写的法国最畅销书之一，这本书讲述了两个11岁的天才逃到威尼斯的爱情故事.笔者以“E＝mc2，我的所爱”为题，是因为E＝mc2是物理学中最伟大、最著名的方程之一.在通俗文化中，能量和质量的关系实际就是相对论的同义语，而提出该方程的爱因斯坦已成为现代物理学的象征.E＝mc2内涵丰富，简洁、大气、优美.面对方程，我们感到庄严、肃穆、敬畏.E＝mc2永远是崇尚科学的人们的所爱.

1 E＝mc2在中学物理中出现的背景

在实施新课程以前的高中物理教科书中，E＝mc2出现在核能这一节，因此学生普遍误认为该方程仅与核能相联系.

实施新课程以后，“相对论简介”被人教版教材安排在高中物理选修3－4第15章，方程E＝mc2第1次出现在该章第3节的末尾：“相对论另一个重要结论就是大家很熟悉的爱因斯坦质能方程E＝mc2，式中m是物体的质量，E是它具有的能量.”就这么简单的一句话.方程E＝mc2第2次出现在选修3－5第19章第5节核力与结合能中，在讲“质量亏损”这一段中有这样一句话：“幸好，爱因斯坦已经给我们指出了物体的能量与它的质量的关系，即E＝mc2.”

可见，无论新旧课程，在高中物理教材中，对方程E＝mc2的来龙去脉都避而不谈，这样，学生对这个方程理解不深，有时会出现误解.我们常会思考这样一些问题：（1）根据爱因斯坦的狭义相对论如何推出方程E＝mc2？（2）如何深刻理解方程E＝mc2？（3）方程E＝mc2一出现就被科学界和社会所认同吗？（4）方程E＝mc2有哪些社会效应（正面的和负面的）和历史遭遇？（5）方程E＝mc2对现代社会有何重要影响？

2 方程E＝mc2的由来

爱因斯坦的质能关系E＝mc2是20世纪的符号.其实，物理学家对质能关系的认识远早于爱因斯坦.牛顿就曾写到：“Are not gross Bodies and Light convertible into one another，…（物体和光之间难道不是可以互相转换的吗）”.其后的岁月，Heaviside和Poincaré都对这个问题作出过回答，Poincaré甚至在1900年得出过质量密度ρ同（假想的）辐射流体的能量密度j之间的关系j＝ρc2.这基本上就可以算是后来的爱因斯坦质能关系了.这个关系常见的解释为“The mass is equivalent to energy（质量和能量是等价的）”.但是，Sachs教授（Mendel Sachs：Concepts of modern physics）认为这不对.爱因斯坦说的是“The inertial mass of matter is a measure of its energy content（（这表明）物质的惯性质量是其能量内涵的测度）”.在相对论的框架内，质能互等式有很多严密的推导，爱因斯坦本人在其一生中就曾对它从不同角度进行多次推导.从不同的角度看待和推导同一个伟大的物理定律，这不是工作的重复，它是非常有趣的和有意义的，因为它们可以增进我们对大自然的“理解”.限于篇幅，下面提供一种推导.

考虑如图1所示的思维实验.图中xB相对xA以速度v做匀速运动，在它们之间的空间中有一个自由漂浮的物体Q，从坐标系xA观察，它是静止的.再建立一个y坐标框架来规定Q的位置.

如果两个完全相同的辐射束R和R′沿垂直于xA轴的直线向着Q运动，并被Q所吸收.从坐标系OxAyA来看，在辐射被吸收以前Q是静止的.根据麦克斯韦电磁理论，能量E的辐射所具有的动量等于是光速.设每一辐射束R和R′的能量均为则动量为由动量守恒定律知，由于每个辐射束以垂直于xA轴的相反方向击中Q，所以Q相对于OxAyA轴显然保持静止.

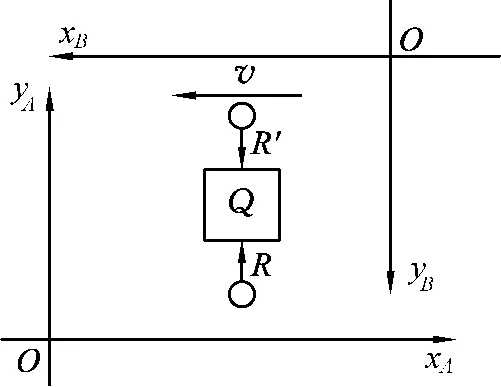
图1

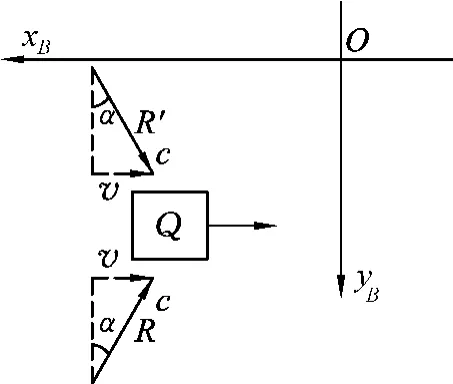
图2

现在从坐标系OxByB来看同样的过程.对于这个坐标系，物体Q以速度v沿xB轴的负方向运动.根据相对论假设——物理定律对各个参考系都是等同的，动量守恒定律在每组坐标系中都是成立的.辐射束R和R′在OxByB中的运动方向如图2所示，它相对于yB轴形成很小的角α，且据坐标系OxAyA中的分析可知，Q吸收辐射束R和R′后，相对于OxAyA轴仍然保持静止.因此，在坐标系OxByB中物体Q的速度在辐射R和R′被吸收以后也保持不变，即物体Q仍然以速度v沿着xB轴的负方向运动，不受空间中物体Q吸收辐射的干扰.

设辐射被吸收前物体Q的质量M，辐射被吸收后Q的质量为M′，在坐标系OxByB中，由动量守恒定律得

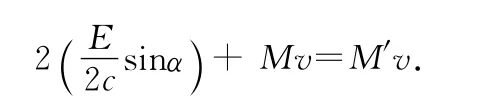
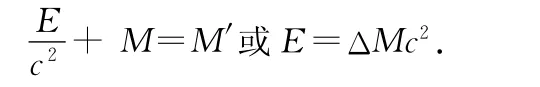
所以，物体质量的改变与吸收的能量成正比.如果选择适当的M和E的单位，则可省略Δ，得到质能方程为

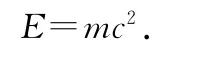
放射性是19世纪最后10年发现的.爱因斯坦意识到，放射性可能是关系式ΔE＝ΔMc2的体现，因为c2是一个非常大的数值，使得一个很小的不可检测的质量损失ΔM，乘上c2时，给出ΔE的数值会是很大的.

3 方程E＝mc2的实验验证

质能关系E＝mc2是狭义相对论的重要结论之一.在核裂变反应和核聚变反应中释放出的巨大能量已准确地证明了该关系的正确性，但科学家们仍拟用实验方法验证此关系究竟精确到什么程度.

1985年美国麻省理工学院（MIT）的 D.Pritchard开始用彭宁捕机（Penning trap）进行测量带电粒子质量的实验.彭宁捕机是一小型实验装置，因荷兰科学家 Frans Michael Penning于1936年设计并制造而得名，其工作原理如图3所示，在强磁场和弱电场的共同作用下，离子在装置内呈现出边上下摆动边绕圈前进的复杂运动形式，测出此摆动的频率便可计算出离子的质量.但外界任何一点机械扰动，都会影响到弧寂离子的“舞姿”，实验工作长期未有进展.直到1999年，尚未大学毕业的D.Fygenson加盟此实验后，Cornell和他改用同时监禁两个不同离子.这时，两个离子以华尔兹舞的方式运动，两者保持一定的距离并合拍地互绕.从而产生了一个类似于双盘天平的效应：考虑两离子的摆动频率之比而不是摆动频率的绝对值，便可互相对照着称量两个离子并对消了外界干扰的影响.但科学家们并未立即使用此技术，此后的大部分工作是致力于单离子彭宁捕机的改进，直到2003年，捕机磁场的不稳定性达到实验所允许的程度时，才把工作转移到两离子消除磁场的起伏.差不多经历了20年之久，Pritchard和他的同事们做到了运用彭宁捕机测定两离子质量之比的准确度达到万亿分之五（5×10－12）.

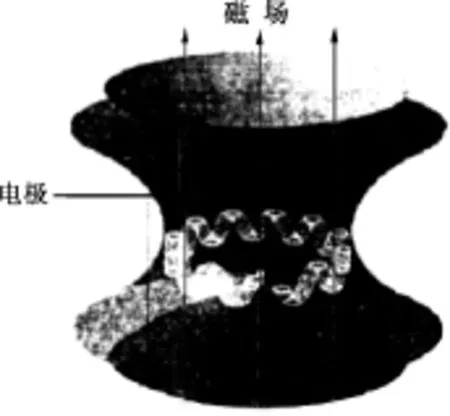
图3

与此同时，美国国家标准和技术研究所（NIST）和法国劳厄－郎之万研究所的科学家们在测量γ光子的能量，在达到准确度接近于（1×10－6）时，并进行比较一个电子加上一个正电子的质量与两者湮灭后释放出的能量的实验，结果得出E＝mc2的误差不到（1×10－5）.此后，MIT小组用彭宁捕机测量放射性硫和硅在它们释放γ射线前后的质量，而NIST小组则用高精度的分光计测量这两个元素放射出的γ射线的波长从而测定射线的能量.双方在肯定了各自测量的准确度后，用电传的方式互递测量数据，得到爱因斯坦提出的E＝mc2接近于完美的程度：E与mc2相差不到千万分之五（5×10－7）.

另外，中科院物理研究所曹则贤先生在《质量和质量的起源》一文中谈到了对方程E＝mc2的实验验证的问题：“关于这个公式的实验验证问题是物理学的一个重要研究内容，但许多研究者却不肯认真对待.2005年世界物理年Nature杂志年终一篇压轴文章，提供的就是对这个问题的实验验证.可惜的是，那只是对ΔE＝Δmc2关系的验证而不构成对爱因斯坦质能关系的验证.……关于这个关系的实验验证，笔者认为逻辑上正确的，是正负电子湮灭实验.”

4 方程E＝mc2和相对论的一些历史遭遇

在爱因斯坦有关质能方程的第一篇论文中，他没有用E来代表能量，E分别是德语“能量”（Energie）或希腊语“能量”（Energia）的首字母，也没有用c代表光速（拉丁语celeritas是迅速的意思）；而是用L代表能量（取自于德语lebendige Kraft，即“活动”能量或动能），用v代表光速.虽然现在我们认为方程E＝mc2中的符号是理所当然的，并已经对它们习以为常了，但是直到1912年爱因斯坦才把方程中的符号改成E和c.

1905年，爱因斯坦的论文发表至少30年之后，控制核能释放的可能性仍被认为是一种幻想.1928年，美国诺贝尔奖获得者R·密立根（Robert Mililkan）在纽约化学家俱乐部的讲话被《先驱论坛报》引用：“人们不可能从原子里放出动力.说我们把煤烧完了就应用原子能，这样轻率的建议是非科学的乌托邦梦想，是幼稚的闹剧.”著名的核物理学家卢瑟福对英国科学进步协会说：“那些在原子转换中寻找新动力源的人，他们的期望只是空想.”《匹兹堡邮报》记者对爱因斯坦的评论被概括成这样的标题：“原子能希望被爱因斯坦夸大了”.

在1920年，一个叫“德国科学家”的保卫纯学术组织，它的最著名的成员是诺贝尔奖获得者P·林诺德（Philipp Lenard）.他们筹组会议，攻击爱因斯坦和相对论；林诺德指出：“（相对论）是犹太人的欺诈行为，有的人也许一开始就怀疑它，他们具有的种族知识比受它浸染的人要多.因为始作俑者爱因斯坦是犹太人.由于许许多多物理学界的突出代表人物多少与犹太人的设计一致，使我愈加失望……在研究自然的犹太人圈子的危险影响中，最重要的例子是爱因斯坦的拙劣的数学修补理论，其中包括一些古代观念和少许任意附加.这种理论现在逐渐成了碎片.”

W·海森伯（W.Heisenberg）在1922年参加了其中的一次公开集会，他在回忆录中写道：“会场是一个大厅，各边都有门.我要进场时，一个年青人（后来知道他是南德大学一个著名物理学教授的学生和助手）塞给我一张红色传单，预先通知我要反对爱因斯坦和相对论.说整个理论只不过是杂乱的推测，它是被新闻界吹捧起来的，与日尔曼精神完全格格不入……我伤心地发现，体弱的和病态的人能够喷发出扭曲了的政治热情，甚至使它进入到科学生命之中”.

德国科学家反犹太人集团的攻击持续多年.1931年出版了一本名为《百位作家反对爱因斯坦》的书，书中一大批德国专家学者所作的批评和林纳德并无二致.

偶尔还有颇受赞誉的物理学家竭力说服他的同事，要他们相信相对论是错误的理论，应当抛弃.打头阵的是H·登格尔（H.Dingle），1922年，他发表他的“问题”和“异议”，反对相对论.尽管有几个权威的相对论物理学家指出他论辩中的缺陷，然而大多数专家避免同他对抗.登格尔贬低这些说理的反响，把大多数人的沉默视为阴谋，说它是本世纪科学衰微的征兆.

还有一些政治性期刊对爱因斯坦的概念进行冷嘲热讽.20年代，《国家》杂志总结说：“（相对论）与阴险毒辣的海蛇是同类……来自战神玛尔斯（Mars）的消息……某些听到引力定律出了问题而心慌意乱的人，不要相信地球会在什么时刻离开牛顿停泊处，漫游到引力之外而进入以太——我们现在听说它是不存在的.”

在前苏联，马赫的观点受到谴责，知识界对爱因斯坦意见分歧.“马赫的哲学对于科学，就如犹大的接吻对于耶稣一样.”苏联专家学者不时地攻击相对论，说它与辨证唯物主义相矛盾，这与他们的有些同事在遗传学上攻击孟德尔主义——摩尔根主义一样.1929年，M·鲍恩（Max Born）在给爱因斯坦的一封信中说到一个年青的苏联物理学家Y·B·鲁默（Y.B.Rumer）在访问了他以后，他得悉：“相对论被认为与官方的唯物主义相抵触……它的信徒受到了迫害.”

英国共产主义者C·考德威尔（C.Candwell）在1930年代后期在他的著作《物理学批判》中论证说：现代资本主义已经崩溃，资产阶级国家的物理学反映了这些国家的意识形态和经济结构，也在瓦解之中.“看来爱因斯坦的世界无疑代表着资产阶级世界观发展的最后产物.”

1952年出版的《苏联哲学辞典》以类似意向描述相对论：“一种反动的对真理的反科学的歪曲……（求助于）神秘主义者和蒙昧主义者，喋喋不休地胡扯四维空间、宇宙的有限性和诸如此类的谬论.只有辩证唯物主义这个无阶级社会的基础可以解决物理学的矛盾.”在斯大林逝世后一段时间，相对论者像孟德尔遗传学者一样，虽然缓慢然而最终抬起头来.到20世纪60年代中期俄罗斯人还出了爱因斯坦文集.

还在爱因斯坦出生之前，就有人推测性地提出关于现代科学发现的危险性的许多预见.T·L·皮科克（Peacock）通过文学著作中的人物之口说道：“Lord Curryfin：因为很清楚，我们有了更多的科学，我们理应更加聪明.Dr.Opimian：科学是一回事，聪明是另一回事.科学像一把锋利的刀，人们像孩子似的玩着它，把自己的手指头给割破了.如果你看一看随着科学成就带来的后果，就会发现它几乎包含所有的有害因素……如果我历数科学带给人类痛苦的罪行，日子就过不下去了.我几乎认为，科学的命运是灭绝人类.”

与此类似，一个世纪之前，J·保罗（J.Paul）写道：“看到化学和物理学的巨大发展，谁能保证最后不会发明出一种穷凶极恶的武器，它类似地雷，发起和停止战斗，在于一发；以致敌人别无选择，只能打出第二发，直到夜晚，整个战斗能够结束吗？”

但是他的同时代人置若罔闻.因此，法拉弟、麦克斯韦、赫兹、开尔文、马赫、霍姆霍兹、洛仑兹等等，没有受到镇压，他们还为爱因斯坦营造了活动舞台.

5 方程E＝mc2与核武器

1905年后的几十年里，方程E＝mc2进入了实验室.1932年，英国剑桥大学著名的卡文迪许（Cavendish）实验室的两位物理学家，即实验物理学家科克罗夫特（John Cockroft）和沃尔顿（Ernest Walton）证明了他们能用加速质子来炸裂锂核.实验证明，得到的锂核各碎片的总质量要比原来的锂核小.起先看起来，质量似乎就这样消失了.但如果测量一下飞散碎片的总能量的话，这两位剑桥的科学家用E＝mc2就能证明锂核破裂后质量变化中所“丢失”的能量正好等于核破裂后高速飞溅的各碎片所包含的能量.爱因斯坦的公式再一次闪耀了光芒.

不过随着人们发现了中子可以引起铀原子核的裂变，方程E＝mc2就被用来改变世界了.多年以来，物理学家迈特纳（Lise Meitner）一直和化学家哈恩（Otto Hahn）一起在德国皇家威廉化学研究所从事研究.那是在树叶茂盛的柏林郊区达勒姆，他们用中子轰击原子核，再用化学方法分拣出反应产物.好多年来，他们和其他人（其中有在罗马做研究的费米小组）已经证实：在轰击之后，他们所看到的反应产物事实上是在元素周期表上铀后的一些新的元素.这些元素被称为“铀后元素”，它们引起了巨大的轰动.这也许是新放射炼金术（radioalchemy）的最伟大的发现.在柏林的这次合作中，他们带到实验室的两种技术相互补充：迈特纳是负责整套设备的物理学家，而哈恩是化学家.但当纳粹迫近，而迈特纳因为是犹太人，她发现自己危在旦夕，两人的密切合作也就毫无意义了.迈特纳最终在1938年7月13日坐火车偷偷逃离了德国.她在瑞典过着十分艰苦的科研生活，焦急地等待着从合作者那里来的消息，而此时整个世界正处在战争的边缘.

在柏林，哈恩继续着试验，实验结果只给他带来更多的疑惑.他和迈特纳早就习惯于见到在一些反应中，由碰撞产生的产物，其性质很像一些比铀要轻得多的元素.不过对于这种现象，哈恩和其他人都认为仅仅是一个化学假象，是不可能发生的——这元素一定在周期表上铀的位置附近.把原子核“撞”成更小的部件是不可能的.可以撞去一个质子或一个α粒子（两个中子将两个质子束缚在一起），但要把原子核正好撞成两份，正像一位物理学家后来所说的那样，就像从窗口扔进一个弹丸来爆破房屋一样.例如，一个反应产物看上去像钡，它很可能就是在化学上同族的镭.接下来情况变得确实古怪离奇了.1938年12月的一个深夜，哈恩写信给迈特纳：“1938年12月19日，周一晚，实验室.亲爱的莉泽.……现在正好是晚上11点；在11点45分施特拉斯曼（Strassmann）（他们的另一位合作者）将会回来，我终于能回家了.实际上关于‘镭同位素’有一些很奇特的情况，现在我们只告诉你一个人……我们镭的一些同位素，它们的性质像钡.”哈恩恳求道：“所以请你想想是否有任何可能”存在一种不同的钡，它比通常的钡要重得多.

在给迈特纳写信3天后，哈恩把文章寄到了出版社.他以一种苦恼的情况结束了文章：他和施特拉斯曼的化学和物理灵魂正激烈地发生着冲突.他们发现一些看上去像是熟悉的轻元素，但又简直不可能：“作为化学家……我们应该用这种［轻元素］符号来代替［我们一直在讨论着的重元素］.而作为相当接近物理学的‘核化学家’，我们却不能使自己跨出这一步，这是与核物理学中此前所有的经验相矛盾的.”

迈特纳收到了这封12月19日的信后，和她的侄子物理学家弗里施（Otto Robert Frisch，他也是逃亡到那里的）在一次去雪中散步时开始揭开信中的谜团.会发生什么呢？他们开始思考，当铀核受中子撞击时，它是否会像一滴大水滴那样开始振动？把原子核看作这样的滴状已经流行了好几年了.他们继续设想整个的微滴通常处于一种相当微妙的平衡之中：它的92个质子相互强烈地排斥着，而其整体却由大约238个质子和中子彼此强烈地吸引的短程核力束缚在一起.所以当它振动时，它可能膨胀，也许会使它变得像一个有黏性的杠铃，在两端各有一个球体，而中间有一个细弱的核柄把它们连接起来.到了这样的膨胀点，位于两个球体中的质子的相互排斥力可能大于能抵消它们的短程核结合力的作用.突然，受到两个球体的电的排斥作用，原子核可能分为两部分，在两头各粗略地有着46个质子的排斥力作用下，两个球体相互飞离.迈特纳计算了一下.两个轻核要比它们在一起时轻.而这一质量差是巨大的，它将按公式E＝mc2转变成能量.她和她的侄子知道了世界上此外无人猜测到的结果：在达勒姆发现了核裂变.

情况发展迅速.被许多同事称为量子理论之父的丹麦物理学家玻尔听说了迈特纳和弗里施的解释后，立即明白此前他的所有推理错在哪里.1939年惠勒和玻尔同船去美国，他也和玻尔一起参加了大西洋两岸物理学家对核裂变所作的综合理论分析.随着原子分裂这一物理重大事件从实验室跃为报纸上头条新闻，一个问题引出了另一个问题.而下一个即将面对的问题对这不稳定的世界是至关重要的：当核分裂时，中子到处飞溅着，是否会导致另外的裂变？铀裂变是否会引起链式反应？如果会的话，由裂变释放的巨大能量将以几何级数增长.不出几个月，就有好几个物理学家开始推测这种裂变过程在不太久的将来会导致制造核弹.爱因斯坦在一些人的请求下，于1939年8月2日给罗斯福总统写了下面这封重要的信：“在过去的4个月里，由于在美国的费米、西拉德（Leo Szilard）和在法国的约里奥（Joliot）的工作，已经有了这种可能性——那就是用大量铀实现核的链式反应，由此可以产生大量能量和许多新的类似镭的元素.现在几乎可以肯定的是这在不久之后就能实现.然而要命的是，它不仅是理论上说能产生能量.这一新现象可以指导我们制造炸弹，这是可信的——即使还不是很确定——可以用这种方法制造出一种新型的威力巨大的炸弹.这种类型的一颗炸弹，用船只携带或在港口里引爆，就完全可以摧毁整个港口及其周围的地区.”

爱因斯坦坚持认为在政府和物理学家之间应保持联系.像给人预兆似的，德国停止了铀的出售.一个代表了科学家立场的中间人在1939年10月1日见到了罗斯福总统，而原子武器的鼓吹者以从匈牙利流亡来的、核链式反应的发现者西拉德所撰写的更专业的备忘录来继续进行他们所关心的事.那时纳粹已入侵波兰，而这一雪球开始其毁灭性的堕落了.大规模的入侵开始了.人们对于德国核弹的恐惧与日俱增；珍珠港遭到袭击；在此事发端后不久，英国筹划了核武器的一个小型规模的工程.美国的一些委员会演变成了实验室，而实验室变成了最大的工厂——在世上曾经见到过的最大的工厂.若干年后，当爱因斯坦回想起那些岁月时，他对在他扶持下才得以开始运转的一切，从道义上进行了深思.他，一开始是一个年轻专利局职员猜测性的涂鸦，然后作为世界上最著名的科学家：“我在一生中犯了一个错误——这就在我写信给罗斯福总统倡议说应该制造原子弹的时候.但我或许可以被原谅，因为我们当时都感到很有可能德国人也在研究这一项目，并可能会成功且用原子弹称霸于世.”

事实上，当爱因斯坦被追问起人们为何能发现原子却不能控制它们时，他回答说：“这很简单，朋友：因为政治远比物理深奥.”

战争结束时，E＝mc2对物理学家来说是原子时代到来的标志——这个时代以结束了强加在他们身上的一次战争而闻名，同时又因促成了一场军备竞赛而遗憾.它同时既是新时代的标志也是所犯错误的一座纪念碑.

E＝mc2无所不在，它是天才的标志，力量的象征，毁灭的先兆.

6 关于质量的起源

中科院物理研究所曹则贤先生在《质量和质量的起源》一文中阐述如下观点：

质量的起源还是个未完全解决的问题.Wilczek教授认为，量子色动力学（QCD）是理解经典力学的基础.物质的质量来自原子，原子质量主要来自核子，核子由夸克组成，但夸克由无（惯性）质量的夸克组成.囚禁夸克的能量在核子层面上表现为质量.这算是对核子质量起源的一个交代，但对电子质量的起源，目前尚无理论上的解释.可能，关于质量的起源，最终还是落在无质量的存在上，有点类似道家的“有生于无”的思想.Wheeler教授（参阅J.A.Wheeler，Geometrodynamics就宣扬“mass without mass”（没有质量的质量）的观点，“to remove any mention of mass from the basic equations of physics（要把质量的概念从所有的基本物理方程中剔除）.”不知这一伟大壮举将来要着落在谁人的肩上.

7 深刻理解方程E＝mc2

质能方程E＝mc2是爱因斯坦在20世纪初对人类社会做出的伟大贡献之一.质能方程揭示了物质的两个属性，即物质的质量和物质的能量间的本质关系，它是近代物理的理论基础.

7.1 质量和能量是物质的两个属性

所谓的物质是指具有能量和动量的客观存在，质量和能量是物质的两个基本属性.爱因斯坦质能方程是建立在相对论理论的基础上，它一方面阐明了质量和能量存在一种对应关系；凡是具有质量的物体一定具有能量、凡是具有能量的物体也一定具有质量.当然，电场、磁场、电磁场、引力场等具有能量的特殊物质也一定具有质量.另一方面说明物体的质量不是一成不变的，而是相对的，当物体的能量发生转化或转移时，物体的质量相应地发生转移.爱因斯坦质能方程说明，在任何物理现象（实际上包括化学、生物现象）中，当能量发生转化或转移的过程中总会伴随着质量的“亏损”或质量的“增加”.

7.2 质量和能量可以相互转化吗

质量和能量是物质的两个不同的属性，是两个不同的物理量，肯定是不能相互转化的.在核反应中释放能量或吸收能量都会导致原子核的质量发生变化，这就是原子核的质量亏损或质量增加.亏损的质量或增加的质量并不是转化成能量，而是相应释放的能量或吸收的能量也具有质量.

7.3 能量的转化或转移中必有质量的转移

自然界中时时刻刻都在发生着各种各样的能量转化和能量的转移.根据爱因斯坦质能方程，在能量的转化或转移过程中必有质量的转移.能量和质量是物质的两个属性，是同一事物的两个不同方面，是不可分割的.物体有能量必有质量，有质量必有能量，物体能量的变化必定相应有质量的变化.“场”有能量也有质量，“场能”变化了相应的质量也要变化.

8 结束语

探究方程E＝mc2的来龙去脉，可以使学生了解孕育时期的科学发展规律，了解科学思想的诞生历程，了解科学家的创造性思维、逻辑思辨能力的形成过程.在物理教学中弄清物理概念、物理规律的建立过程有助于学生探索精神、创新能力的培养.物理学科的魅力不仅在于知识本身，而且在于它的科学思维方法、研究方法、科学素质和创新精神.物理教学要培养学生自己获得知识的能力，就要让学生从物理规律的发现过程得到启迪，学会思考，学会探索.因此物理教学的重点应该使学生领悟理论规律的发展历程，它起始于哪里，过程如何，怎样突破等等，让学生感受物理学家的思路历程，使学生学会思考、学会应用、学会创新.

1 Irving M.Klotz著.何常译.天堂的钥匙也开启地狱之门：相对论和E＝mc2.Science Progress，1998（1－2）.

2 许槑.对E＝mc2的实验验证.物理通报，2007（1）.

3 包向飞.质能互等式E＝mc2的一个简单推导.科学之友，2009（10）.

4 唐衡发.对质能方程的理解.中学物理教学参考，2005（5）.

5 曹则贤.质量与质量的起源.物理，2008（5）.

6 曹则贤.平、等与方程.物理，2008（12）.

7 赵峥.相对论百问（第1版）.北京：北京师范大学出版社，2010.

8 赵峥.探求上帝的秘密（第2版）.北京：北京师范大学出版社，2009.7（2）.

9 爱因斯坦.相对论.北京：北京出版社，2007（10）.

10 李宏魁.爱因斯坦质能方程的一种推导.高等数学研究，2001（5）.

11 ［英］格雷厄姆·法米罗主编，涂泓吴俊译，冯承天译校.天地有大美 现代科学之伟大方程（第1版）.上海：上海科技教育出版社，2006.