审视物理情境构建物理模型
陈 锋
(南京师范大学附属中学,江苏 南京 210003)
学生在学习高中物理必修2的“宇宙速度”内容时会有这样的疑问,如果物体以第一宇宙速度抛出但速度方向不是水平,能成为绕地球运行的人造地球卫星吗?如果物体以第一宇宙速度竖直向上抛出能脱离地球的引力束缚,成为绕太阳运行的人造行星吗?……要回答这些问题,不仅需要有关天体运动规律的知识,还需掌握解决这类问题的有用的模型与方法,常用的有以下几种.
1 圆轨道模型
在忽略大气阻力的情况下,物体在地球表面附近至少以多大的水平速度抛出,就不再落回地面成为绕地球运动的人造卫星?如图1所示,设地球质量为M,地球半径为R,物体质量为m,物体沿地球表面匀速运动的速度为v,运行的周期为T,万有引力常量为G,本文字母表示相同的含义.
物体沿地球表面的运动可看成匀速圆周运动,地球对物体的引力提供物体做圆周运动所需的向心力,即得物体运动的周期为

图1

这个速度就是第一宇宙速度,当发射的速度大于7.9 km/s小于11.2km/s时物体将成一颗绕地球运行的人造地球卫星.在高中阶段研究天体运动时一般都把天体运动的椭圆轨道近似看成圆轨道,万有引力提供天体做圆周运动所需的向心力.
2 极限轨道模型
当物体以第一宇宙速度竖直向上抛出时,物体经过多长时间上升到最高点?上升的最大高度多大?
通常情况下,研究地面附近物体竖直上抛运动时,由于抛出时的速度较小,上升的高度有限,可以认为物体做匀变速直线运动.当物体抛出的速度很大,上升的高度很高时,万有引力的变化对物体运动的影响不能忽略,这时可建立极限轨道模型.如图2所示,把物体运动的轨道看成很扁的椭圆轨道,椭圆短轴2b趋于0,地心为椭圆的一个焦点,近地点、远地点与两个焦点距离很小,几乎重合,则最高点与地心的距离等于椭圆的长轴2a.
由机械能守恒定律得

第一宇宙速度为

由(1)、(2)式解得a=R.所以物体上升的最大高度为h=R.
由开普勒第二定律得

式中S阴影是物体运动时间t内,物体与地心连线扫过的面积,等于半个椭圆ABC面积与三角形AOC面积之和(如图2中阴影部分).


图2
由(3)~(5)式得

由开普勒第三定律得绕地球运动半长轴为R的椭圆运动的周期和绕地球运动半径为R的圆的周期相等,则

又第一宇宙速度为

由(6)~(8)式解得

物体以第一宇宙速度竖直向上抛出时,物体经过时间
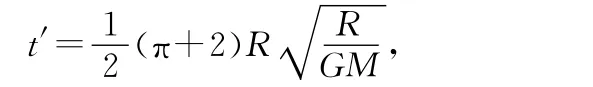
上升到最高点,上升的最大高度等于地球半径R.
物体竖直向上发射的速度很大但小于第二宇宙速度时,物体运动轨道可看成是椭圆轨道的极限:短轴趋于零,长轴等于地心与最高点之间的距离这一模型进行研究.
3 椭圆轨道模型
物体从地球表面附近A点抛出时速度大小等于第一宇宙速度,方向与与竖直方向成θ角,在地球对物体的万有引力作用下物体将沿椭圆轨道运动,地心O为椭圆的一个焦点,远地点B与地心O距离为r,物体经过远地点B时速度为vB,如图3所示.
由开普勒第二定律得Rvsinθ=rvB,所以

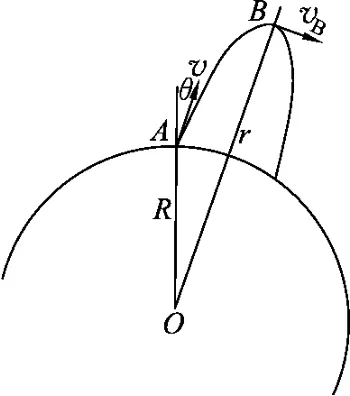
图3
又第一宇宙速度为

由机械能守恒定律得
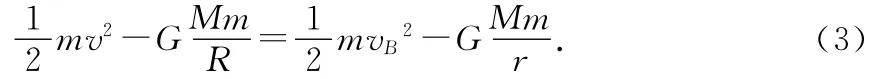
把(1)、(2)式代入(3)式并化简,得

解得r1=R+Rcosθ或r2=R-Rcosθ,r1对应椭圆轨道的远地点,r2对应椭圆轨道的近地点,B点到地心的距离为r1=R+Rcosθ,则物体能上升的最大高度为h=R+Rcosθ-R=Rcosθ.
椭圆长轴2a=r1+r2=2R,焦距2c=r1-r2=2Rcosθ,短轴,建立如图4所示坐标系,椭圆方程为
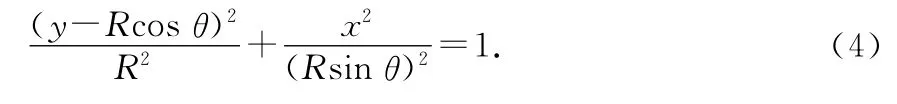
圆方程为


图4

图5
由(4)、(5)两式解得x=±Rsinθ,y=Rcosθ.
物体落地点与抛出点间的距离等于圆弧AC的长度,即s=2Rα=2Rθ.
物体飞行的时间由开普勒第二定律得

式中面积St是物体运动时间t内,物体与地心连线扫过的面积,等于半个椭圆ABC面积与三角形AOC面积之和,如图5所示.

由开普勒第三定律,绕地球运动半长轴为R的椭圆运动的周期和绕地球运动半径为R的圆的周期相等T=,代入
当θ=0°时,即物体竖直向上抛出,飞行时间为
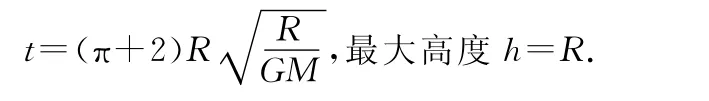
当θ=90°时,即物体水平抛出,飞行时间为
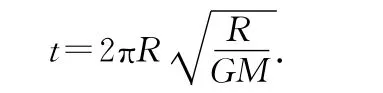
当物体发射的速度很大但不大于第一宇宙速度时,万有引力的变化对物体的运动影响不能忽略,物体不再作一般意义上的斜抛运动,而是沿椭圆轨道运动,最终落回地球表面.

