何处速度最大

贾开鹏

（陕西省洛南中学，陕西 洛南 726100）

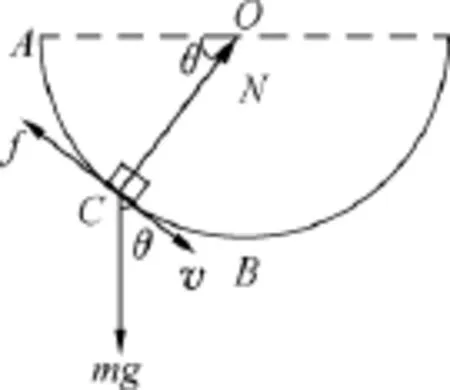
图1

有这样一道力学题：如图1所示，一物块从半圆形轨道顶端无初速滑下，当物体通过最低点时，速度为v，已知物体和轨道间的动摩擦因数为μ，圆轨道半径为R，则物块滑过最低点时受到的摩擦力为多少？并讨论在下滑过程中，何处速度最大？

这是一个常规的题目.第1问，根据圆周运动及牛顿第二定律，很容易解决；对于第2问，许多人认为，在最低点速度最大.笔者对后一问，用2种方法分析.

方法1：定性分析法.

在物体下滑过程中，改变速度大小的原因是合外力切向分量，即产生切向加速度.下滑过程中，合力切向分量是重力的切向分量与滑动摩擦力的合力，方向先与速度方向一致，而在最低点仅有滑动摩擦力，方向已经反向.说明在下滑到最低点之前的某点，存在切向合力为0的瞬间，该点速度应该最大.

下面再用定量计算的方法，分析何处速度最大.

方法2：运用动能定理定量分析.

设物块从A点无初速滑下，物块与圆心连线半径和水平方向夹角为θ时的C点，瞬时速度为v，此时对物块由牛顿第二定律，得

在此过程中，由动能定理得

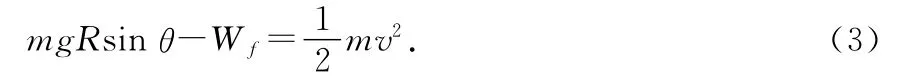
（3）式中Wf是物块克服摩擦力做的功，是变力功，需要用到积分来处理.

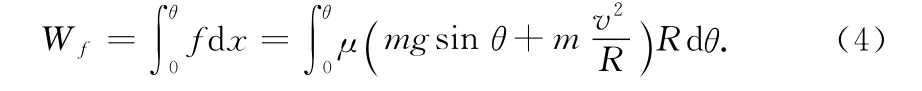
（4）式经计算可得

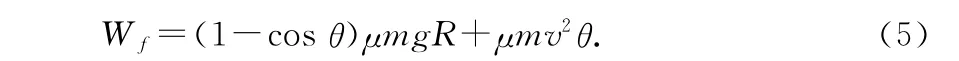
将Wf代入（3）式可得

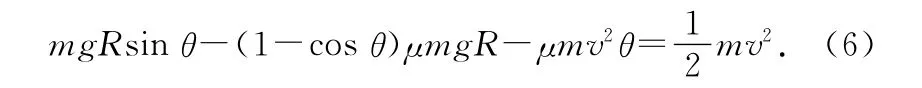
解得

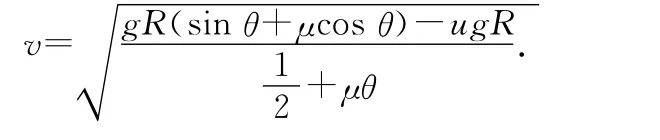
也可进行数学变形得

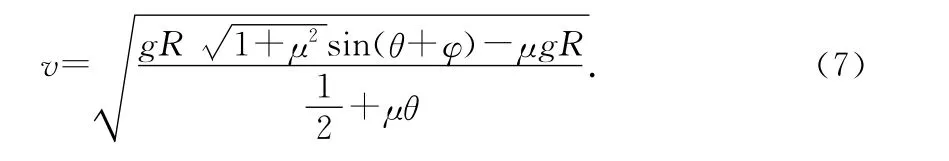
为了更加直观地表示速度的变化，也可以用Excel图表软件作出v2－θ图像如图2所示.作图时取g＝9.8m／s2，μ＝0.5，R＝0.2m，在区间，可以发现v2随θ先增大后减小，完全验证了上述推理.

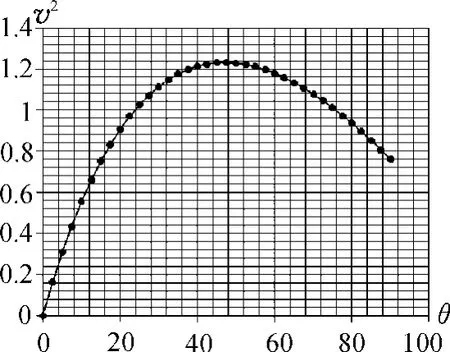
图2