“气体分子单位时间内与单位面积器壁碰撞次数”问题探讨

张韶朗

（江苏省灌南高级中学，江苏 连云港 222500）

在高中物理现行人教版教材选修3—3中，有关气体压强的微观意义，用“雨点打伞”来类比“气体分子碰撞容器壁”（如图1），说的简单明了.气体对容器的压强是大量气体分子对容器的碰撞引起的，这就好像密集的雨点打在伞上一样，雨点虽然是一滴一滴地打在伞上，大量密集雨点的撞击，使伞受到持续的作用力.同时教材中还配了演示实验，用“竹筒倒豆粒，豆粒下落击打台秤托盘”来模拟气体压强产生的机理（如图2），并定性分析影响气体压强的两个微观因素，在相同高度下改变单位时间内竹筒倒落豆粒的颗数，可得出单位时间内落到托盘的颗数越多，台秤示数越大；在保证单位时间内竹筒倒落豆粒颗数一定的前提下，改变竹筒高度，调节豆粒撞击托盘时的动能，可得出：高度越高，动能越大，台秤示数越大.故可得出影响气体压强的两个微观因素为气体分子的平均动能和密集程度.

图1

图2

教材对于压强的微观解释形象生动，浅显易懂.但是对于相关内容的考查却让很多师生焦头烂额，“气体分子单位时间内与单位面积器壁碰撞次数”问题就是一例.鉴于此，本文针对该问题作一粗浅的分析，以飨读者.为阅读方便，笔者将“单位时间内单位面积上”简称为“双单”.

1 根据两决定因素分析

如图3，在恒温环境下，将一导热性良好的气缸封闭一定质量的气体.在保持体积不变的情况下，缓慢向该容器内注入同种气体，如图4所示；或者缓慢推动气缸活塞，使其容积减小，如图5所示.这两种情形均是在气体温度保持不变的前提下，增大了单位体积内的分子数，即增大了分子的数密度，使得“双单”器壁上的碰撞次数增加了.若在保持气缸容积不变的情况下，升高外界环境温度，使得密闭容积内的气体温度升高，分子运动平均速率增大，则“双单”器壁上的碰撞次数也会增加.因此“双单”器壁上的碰撞次数决定于气体分子的数密度和平均速率两个因素.

图3

图4

图5

下面举例说明.

例1.（2011年南京盐城模拟试题）给旱区人民送水的消防车停在水平地面上，在缓慢放水的过程中，若车胎不漏气，胎内气体温度不变，不计分子间作用力，则胎内__________热量（填“吸收”或“放出”），单位时间内单位面积的车胎内壁受到气体分子平均撞击次数__________（填“增加”、“减少”或“不变”）.

答案：吸收、减少.

解析：第1空略.缓慢放水，胎内气体等温膨胀，温度不变，分子平均速率不变；体积变大，分子的数密度减小.故“双单”器壁上的碰撞次数减少.

（2）仅改变分子平均速率.

例2.（2011年盐城中学模拟试题）下列说法中正确的是

（A）被活塞封闭在气缸中的一定质量的理想气体，若体积不变，压强增大，则气缸在单位面积上，单位时间内受到的分子碰撞次数增加.

面板数据具有截面和时间序列二维特性。回归模型可以分为随机效应模型、固定效应模型、混合效应模型等。其中固定效应又可以细分为截面固定效应和时间固定效应。对固定效应的选择，通常做法为若截面数据存在异质性，则用截面虚拟变量来控制异质性；若时间维度数据存在异质性，而截面维度较稳定，则引入时间虚拟变量进行估计。刘学良等探讨了面板数据固定效应模型回归的本质，时间固定效应是有线性约束的截面回归，它的回归表现为样本在截面维度的相关关系，回归结果等于截面回归估计的加权平均［12］。人力资本变量在各商业银行时间维度存在异质性，因此选用时间固定效应模型，即时间不同，模型的截距不同。模型矩阵如下：

（B）晶体中原子（或分子、离子）都按照一定规则排列，具有空间上的周期性.

（C）分子间的距离r存在某一值r0，当r大于r0时，分子间斥力大于引力；当r小于r0时分子间斥力小于引力.

（D）由于液体表面分子间距离大于液体内部分子间的距离，液面分子间表现为引力，所以液体表面具有收缩的趋势.

答案：（A）、（B）、（D）.

解析：（B）、（C）、（D）项略.（A）项中，气体质量一定，体积不变，压强增大，据气体状态方程可得温度升高.体积不变，分子数密度不变；温度升高，分子平均速率变大.故“双单”器壁上的碰撞次数增加.

（3）分子数密度和平均速率同增同减.

例3.（2011年苏北四市模拟试题）如图6，一气缸内用活塞封闭一定质量的理想气体，现用力F使活塞迅速地向下移动，密闭气体的状态发生了变化，则变化后较原来单位时间内气体分子对单位面积的器壁碰撞次数_________（填“增加”、“减少”或“不变”）.

答案：增加.

解析：“迅速”表示过程进行得很快，来不及发生热传递，等同于“绝热”.因此可以当作绝热压缩过程，外界对气体做功，气体内能增加，温度升高，分子平均速率变大；体积变小，分子数密度变大.故“双单”器壁上的碰撞次数增加.

以上3例均可用两决定因素定性解决，但是此方法在升温膨胀或降温压缩情况下却是行不通的，因为会导致分子数密度和平均速率存在互为消长的关系，故最终结果无法获知.此时我们要另辟蹊径，从气体压强的微观意义来考虑.

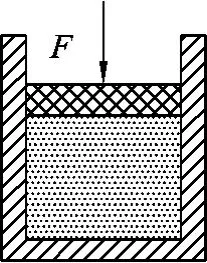
图6

2 根据压强微观表达式分析

设想有一个向右运动的气体分子与器壁发生弹性碰撞，如图7所示，碰撞前后的速度大小均为v，但是方向相反.选取向右为正方向，则碰撞前后分子的动量变化为－mv－mv，即为－2 mv.据动量定理，这个动量变化等于器壁对分子的冲量，又据牛顿第三定律，分子对器壁也有一个等量反向的冲量2 mv.故分子每碰撞一次器壁，就给予器壁2 mv的冲量.

图7

任意选取一处面积为S的容器壁，设在时间t内共有N个分子撞击容器壁，则据动量定理可得故压强式中表示在单位时间内单位面积上与器壁碰撞的分子数，令为D.因此压强表示单位时间内单位面积器壁所获得的平均冲量，简记为p＝D·2 mv.本式虽然仅是一个单靠力学未用统计规律推导的压强公式的“半成品”，但对于定性分析本类“双单”问题却显得非常简单.

例4.（2011年江苏调研试题）一定质量的理想气体被封闭在气缸内处于平衡状态Ⅰ，现设法使其温度升高同时压强减小，达到平衡状态Ⅱ，则由状态Ⅰ变为状态Ⅱ的过程中，单位时间内气体分子对器壁单位面积的碰撞次数__________（填“增加”、“减少”或“不变”）.

答案：减少.

解析：温度升高，分子平均速率变大，但压强减小，由式p＝D·2mv可知D减少.或者可将分子比作拳击运动员的拳头，速度越大，拳头给予对方的作用力越大，但是要想压强减小，只能靠减少单位时间内出拳的次数.

点评：笔者发现，利用p＝D·2 mv能顺利解决（1）、（2）类问题，但对（3）类问题也束手无策，故也有其不足之处.

3 理论推导

建立直角坐标系，用v表示气体分子的速度矢量，用vx表示v沿坐标轴x的分量.据麦克斯韦速度分布律可知，在平衡状态下，气体分子的速度分量vx在区间vx～vx＋dvx内的分子占总分子数的比率为

现在垂直于x轴的器壁上取一小块面积dA，设单位体积内的气体分子数为n，则单位体积内速度分量vx在区间vx～vx＋dvx内的分子数为nf（vx）dvx，在这些分子中，在一段时间dt内能够与面积dA的器壁相碰的分子只是位于以dA为底、以vxdt为高的柱体内的那一部分气体分子，其数目为nf（vx）dvx·vxdtdA.因此，单位时间内碰到单位面积器壁上速度分量vx在区间vx～vx＋dvx之间的分子数即为nvxf（vx）dvx.又vx＜0的分子不会与dA相碰，只有vx＞0的分子才有可能与dA相碰，所以将上式从0到∞对v积分，即可求得“双单”器壁上的分子总数为

4 总结

本文重点阐述了“双单”气体分子单位时间内与单位面积器壁上的碰撞次数的决定因素，从定性分析到定量推导，结合具体问题进行分类讨论，并借助气体压强微观意义，对压强进行深入的定量剖析，得出解决“双单”问题的又一方法.

解决“双单”问题要靠“两把剑”：一把是决定因素，另一把是压强的微观表达式.这“两把剑”各有利弊，只有双剑合璧，才能迎刃而解.

1 李椿，章立源，钱尚武编.热学（第1版）.北京：高等教育出版社，1978.

2 人民教育出版社，课程教材研究所，物理课程教材研究开发中心编著.普通高中课程标准实验教科书物理（选修3—3）（第3版）.北京：人民教育出版社，2010.