基于心音信号的生物识别技术研究

□杨 勇，郭兴明

（1．重庆市公安局渝中分局，重庆 400010;2．重庆大学 生物工程学院，重庆 400030）

随着社会的发展，安全问题日趋重要，用人类生物特征并结合计算机技术进行安全验证的生物特征识别技术已成为当今的热门课题。生物特征识别技术是根据每个人独有的可以采样和测量的生物学特征和行为学特征进行身份识别的技术。由于生物特征不像各种证件类持有物那样容易窃取，也不像密码、口令那么容易遗忘或破解，所以在身份识别上体现了独特的优势，近年来在国际上被广泛研究。［1］作为人体特征之一的心音信号，反应人体的许多生理特征，也可以作为一种生物特征达到身份识别的目的。［2］

心音特征识别认证过程中最主要的两部分内容是特征提取和模式匹配。［3］特征提取，就是从心音信号中提取到惟一表现受试者身份的有效且稳定可靠的特征;模式匹配就是对训练和鉴别时的特征模式做相似性匹配。由Davies和Mermelstein提出的Mel倒谱系数（MFCC）已经被证明为在语音相关的识别任务中应用最成功的特征描述之一，可以作为心音特征识别认证的重要特征参数。

一、MFCC特征提取

（一）预处理

实验中对含噪心音信号的预处理部分包括:滤波、预加重、分帧和加窗。［4］

1．滤波

心音信号是由心肌收缩和舒张，以及心脏瓣膜、室壁和大血管在血流冲击下形成的振动经胸腔传导至体表，用听诊器等设备采集到的声音。因此，心音信号中的噪声主要来自环境噪声、工频噪声、仪器本身的声音等。提取心音信号特征参数前首先要对心音信号进行去噪处理。［5］

2．预加重

在实际信号分析中常采用预加重技术，即在对信号取样之后，插入一个一阶的高通滤波器，以滤除低频干扰，突出更为有用的高频部分的频谱。本实验使心音信号通过系统函数为H（z）=1－az－1的数字滤波器，a为预加重因子，取0．975。

3．分帧和加窗

心音信号是一种短时非平稳信号，要对其进行短时分析，需要对信号进行分帧，然后再用一个有限长度的窗序列W截取一段信号来分析。频域分析时常采用的是哈明窗，在分帧和加窗的基础上即可对心音信号进行特征提取等处理。

（二）Mel倒谱系数的提取

Mel频率倒谱系数（Mel－Frequency Cepstrum Coefficients，MFCC）是广泛应用于语音相关识别的特征参数。MFCC和线性频率的转换关系如下:

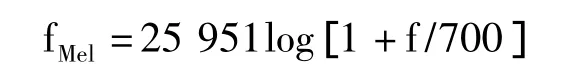
MFCC参数是按帧计算的，其提取过程如图1 所示。

图1 MFCC的提取过程

Mel滤波的作用是利用三角形滤波器组对语音信号的幅度平方谱进行平滑;对数操作（log）的作用有两点:其一是压缩心音频谱的动态范围，其二是将频域中的乘性成分变成对数谱域中的加性成分，以便滤除乘性噪声;离散余弦变换（DCT）主要用来对不同频段的频谱成分进行解相关处理，使得各向量之间相互独立［3］P28－30。

其中Mel频率滤波器组为在语音的频谱范围内设置的若干个带通滤波器Hm（k），0≤m＜M，M为滤波器的个数，取为24。每个滤波器具有三角形滤波特性，其中心频率为f（m），当m值小时相邻f（m）之间的间隔也小，随着m的增加相邻f（m）的间隔逐渐变大。每个带通滤波器的传递函数为:

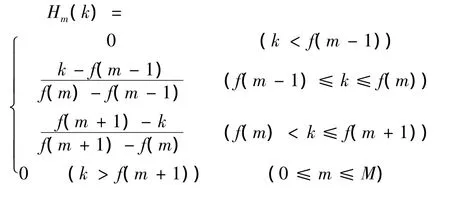
二、高斯混合模型GMM

高斯混合模型（Gaussian Mixture Model，简称GMM）是单一高斯概率密度函数的延伸，［6］它的优点是可以平滑地逼近任意形状的概率密度函数，并且是易于处理的参考模型，相当稳定。该算法复杂度较低，实时性好。

GMM参数的训练一般采用最大似然（ML:Maximum Likelihood）估计的方法。设某受试者心音信号的训练特征矢量序列为X={xt，t=1，2，…，T}，它对于模型λ的似然度可表示为:

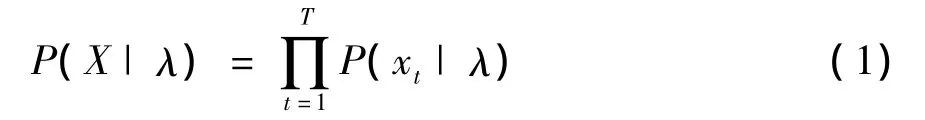
训练的目的就是找到一组参数λ，使P（X|λ）最大，即:

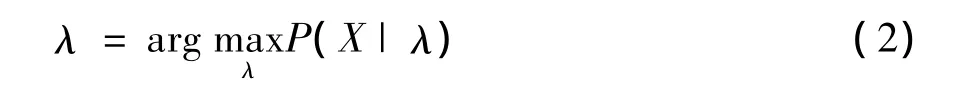
P（X|λ）是参数λ的非线性函数，直接求其最大值是不可能的。这种最大参数估计可利用EM算法通过迭代计算得到。［7］

每个识别对象用一个GMM模型来代表，分别为 λ1，λ2，…，λS。在对其进行身份辨认时，目的就是对一个观测序列X，找到使之有最大后验概率的模型所对应的受试者 λS［7］P259－261，即:

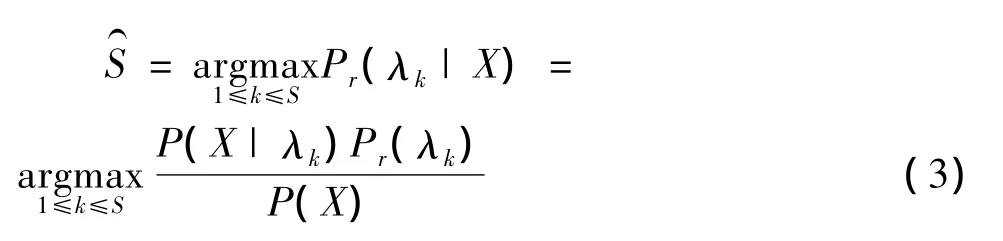
假定Pr（λk）=1/S，即每个受试者出现为等概率，且因P（X）对每个受试者是相同的，上式可以简化为:

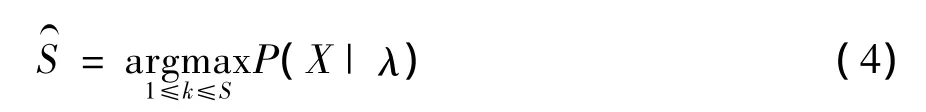
如果使用对数得分，且按式（1）假定，受试者辨认的任务就是计算

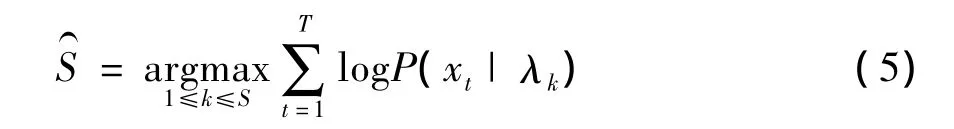
用GMM模型对心音特征参数进行训练时，必须选择合适的模型阶数。GMM的阶数越高，GMM模型的声学分辨率越高，能模拟的分布也就越复杂，鲁棒性越好。但阶数太高，无论从GMM参数估计的处理速度上，还是从说话人模型的存储容量上，都是不易接受的。同时，在等量的训练数据下，GMM模型的阶数越高，用于估计GMM中的每一个高斯分布的训练样本数就越少，GMM参数估计的精度也就越低。［8］因此，需要选择能保证系统性能的最优的GMM阶数。

三、实验结果及分析

本文采用的心音识别模型为高斯混合模型（GMM），试验中训练和识别的心音信号是由JXH－5型数字心音传感器采集得到的。采样频率为11025Hz，量化精度为8bit，共选取了50个人的心音信号作为识别对象。实验中记录每个人静息状态下40s的心音信号，其中前20s用于训练，后20s用于识别。该实验的原理，如图2所示。

（一）心音信号的预处理

实验环境为美国Mathworks公司开发的新一代科学计算软件MATLAB7．0。输入的心音信号首先使用端点检测，检测到S1，S2的位置，如图3所示。然后用预加重滤波器H（z）=1－0．975z－1进行预加重，如图4所示。实验表明，预加重可以有效地提高系统的性能。

图2 心音识别认证系统流程图

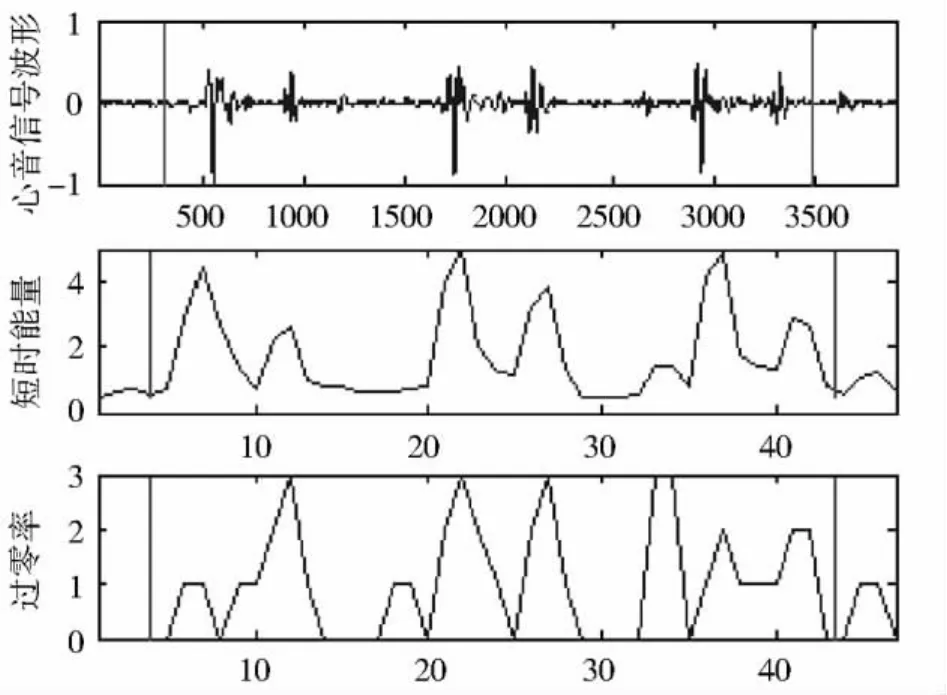
图3 心音信号的端点检测结果

本实验采用的是双门限端点检测算法，在开始端点检测前，先要分别为短时能量和过零率确定两个门限。如果信号的能量或过零率超过了低门限，就开始标记起始点，进入过渡段。在过渡段中，由于心音信号的参数数值比较小，不能确定是否进入了有用信号段，只要两个参数的数值都回落到低门限以下，就将当前状态恢复到静音状态，而如果在过渡段中两个参数中的任一个超过了高门限，就可以确信进入了有用信号段。

从图4可以看出，信号经过预处理后，原始信号的低频干扰得到了抑制，而更为有用的高频部分的频谱得到了提升。

实验中采用哈明窗函数对心音信号进行分帧，取帧长20ms，帧移为10ms（即每相邻两帧之间有半帧是重叠的，以保证帧与帧之间的平滑过渡，保持其连续性）。计算中利用了MATLAB中哈明窗函数（hamming），采用MATLAB的语音分析工具箱VoiceBox，可以很容易地对心音信号进行分帧处理，其分帧函数调用为:f=enframe（x，256，128）。

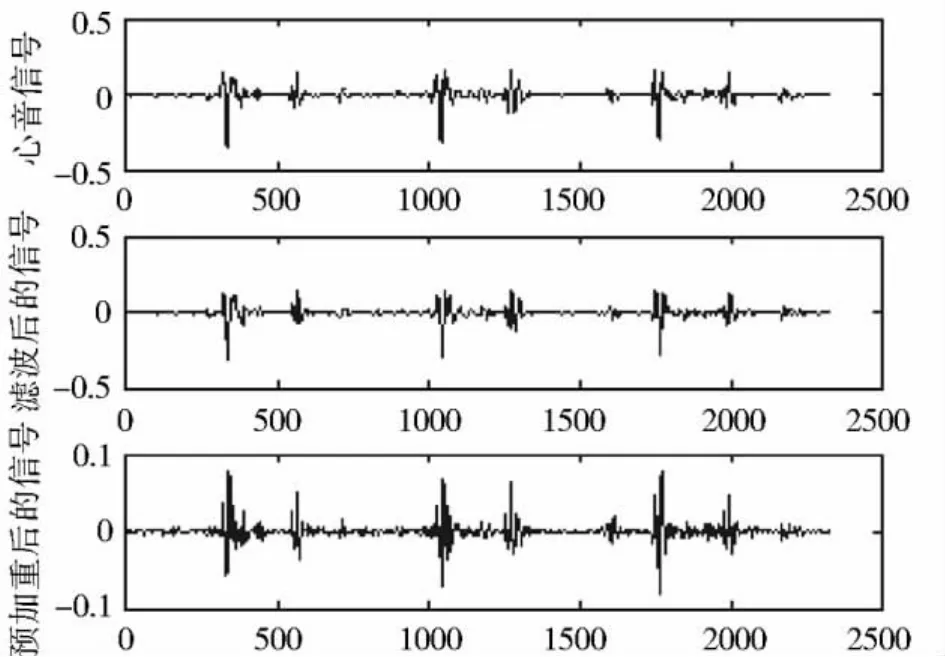
图4 滤波后和预加重后的信号比较

（二）基于MFCC和GMM的生物识别的实现

本实验选取了MFCC参数的前面16个系数（C0～C15）如图5所示，图中x轴表示心音信号分帧的帧数，y轴表示倒谱系数的维数，z轴表示对应的倒谱值。提取得到的MFCC作为GMM模型训练的输入特征矢量。

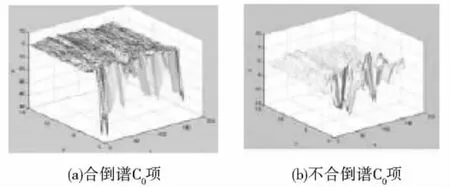
图5 MFCC参数

前文提到，GMM模型的阶数是影响系统性能的一个重要指标，阶数过小，量化误差太大，高斯混合模型不能很好地表示整个向量空间;而阶数过大，训练和测试的计算量都会非常的大，而且对性能没有显著提高。［9］图6为不同 GMM阶数下系统的识别率。

图6 不同GMM阶数下的识别率

由图6可以看出，64阶GMM可以达到和32阶GMM一样的识别率，但是计算时间却增加了很多，因此并不是盲目地加大GMM阶数就能提高系统性能的。在综合考虑系统总体性能的基础上，将GMM的阶数选为32阶。

四、结束语

本文运用MATLAB实现了基于心音信号的身份识别认证，并进行了相关测试。实验中，共采集了50个人的心音信号，对该算法进行测试，经过反复实验，认为该算法具有良好的抗噪性能，并取得了满意的识别率。但是系统中采用的样本数量较少，样本训练时间较短，这对系统提高识别率有一定的遏制作用，有待于在以后的工作中解决这个问题。

［1］A，K．Jain，A，Ross，S．Prabhakar，An introduction to biometric recognition，IEEE Trans．Circuits Syst．Video Technol，2004（1）:4 －20．

［2］Koksoon Phua，Jianfeng Chen，Tran Huy Dat，et．al．Heart sound as a biometric．Pattern Recognition，2007:1 －14．

［3］王华朋，杨洪臣．声纹识别特征MFCC的提取方法研究［J］．中国人民公安大学学报（自然科学版），2008（1）:28 －30．

［4］吴华玉，曾毓敏，李 平．一种具有鲁棒特性的Mel频率倒谱系数［J］．金陵科技学院学报，2008（2）:26－29．

［5］郭兴明，吴玉春，肖守中．自适应提升小波变换在心音信号预处理中的应用［J］．仪器仪表学报，2009（4）:802－806．

［6］Rong Zheng，Shuwu Zhang，Bo Xu．Text－ independent speaker identification using GMM－UBM and frame level likelihood normalization［J］．Chinese Spoken Language Processing，2004 International Symposium on，2004，12:289 －292．

［7］易克初，田 斌，付 强．语音信号处理［M］．北京:国防工业出版社，2000:259－261．

［8］辛全超，吴 萍．基于GMM的说话人识别研究与实践［J］．计算机与数字工程，2009（6）:11－15．

［9］胡益平．基于GMM的说话人识别技术研究与实现［D］．厦门:厦门大学，2007．