基于地层线的三维地质剖切算法

黄 忠， 江巨浪， 张佑生

（1.安庆师范学院 物理与电气工程学院，安徽 安庆 246011；2.合肥工业大学 计算机与信息学院，安徽 合肥 230009）

基于地层线的三维地质剖切算法

黄 忠1，2， 江巨浪1， 张佑生2

（1.安庆师范学院 物理与电气工程学院，安徽 安庆 246011；2.合肥工业大学 计算机与信息学院，安徽 合肥 230009）

文章以地质钻孔为离散点，运用空间插值以及由曲面拟合得到的各地质结构趋势面，建立了工程地质三棱柱结构模型，在此模型基础上提出一种任意切面的剖切方法。该方法首先应用三维空间求交算法快速求出剖切面与凹凸起伏的地层趋势面的交点；然后将这些交点按照地层层序连接成三角形并根据其贯穿的地层属性进行精确着色，从而得到三维的剖切实体图、切面图，为地质工作者在3D空间中观察地质结构、分析地质特征提供了新的方法和手段，可为地质工程项目的设计、管理和施工提供科学的决策依据。

地质结构趋势面；空间求交；剖面；倾斜剖切；剖切分析

一般地，各种地质信息，包括地表地形、地层界面、断层、地下水位、风化层厚度分布以及各种物探化探资料，都可以通过野外测量获得。这些信息是一些离散的数据，地质工作者很难直接利用它们分析其在地质体中的分布规律［1］。研究者们面对这些实测信息，利用趋势面拟合或空间内插的方法获得地质结构趋势面，再根据三维地质体特征，采用属性插值、地质解译、评估分析、统计预测等方法建立三维地质模型，然后运用可视化算法，对数字仿真模型进行处理，绘制出具有真实感的三维地质结构图。由于不同地层面是由规则网格分解成三角网组成，而这些三角网在水平面上的投影是相同的，这样使得相邻层对应三角形和竖直方向上互相平行的3条棱边就构成了三棱柱结构［1］，如图1所示。

建立了工程区地质体三棱柱模型后，将同层的三棱柱着以相同的颜色，不同层的三棱柱着以不同颜色，通过颜色反映地质特征的变化，达到直观描述地下复杂的地质构造情况，形象地表达地质构造的形态特征的目的。但为了展示地质体内部特征、空间特征并对其地质特征进行综合分析，还需要对地质体进行三维的剖切，以便清晰地展现模型的内部细节，最大限度地增强地质分析的直观性和准确性［2］。因此，三维工程地质模型剖切的实现一直是研究的热点［3］。

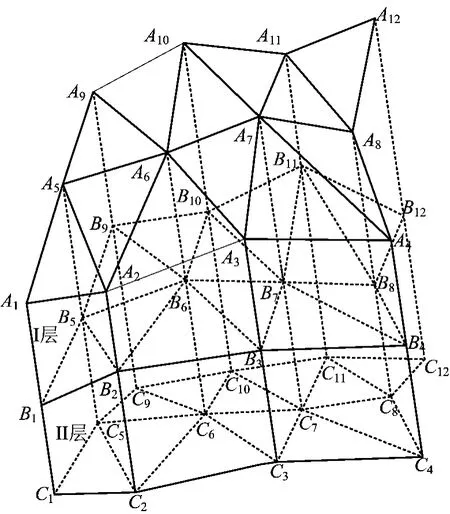
图1 地质体三棱柱结构

目前，工程地质三维剖切主要有2种途径：

（1）求构成三维地质模型的不规则三角形面与空间剖切平面的交线，这种算法需要搜索所有的面与线，计算量大、时间长［4］。

（2）采用投影方法，将三维离散钻孔点集转化为二维平面点集［5］，这种算法违反Delaunay三角剖分“最大最小角”优化准则［6］。

基于上面2种方法的特点，本文提出基于地层线的三维地质剖切算法，以实现任意剖面的三维剖切分析，这需要有效地解决如下2个问题：

（1）快速求出剖切面与凹凸起伏的地层面的交点。

（2）根据不同地层线的交线绘制出反映地层属性的剖面。

1 地层面与剖切面求交算法

考虑地质体的三棱柱结构，对三维地质体的剖切变成对三棱柱的剖切，其实质是对剖面与上下三角面片和棱柱侧面求交［7］。但地质体中含有大量的三棱柱，每个三棱柱将与剖切面进行5次面面求交测试［8］，其计算量在交互环境中是无法接受的。因此，当求地层面与剖切面的交线时，首先用三角网格逼近地层面，然后用这些近似三角网格与剖面的交线来近似表示地层面和剖切面的交线，如图2所示［9］。

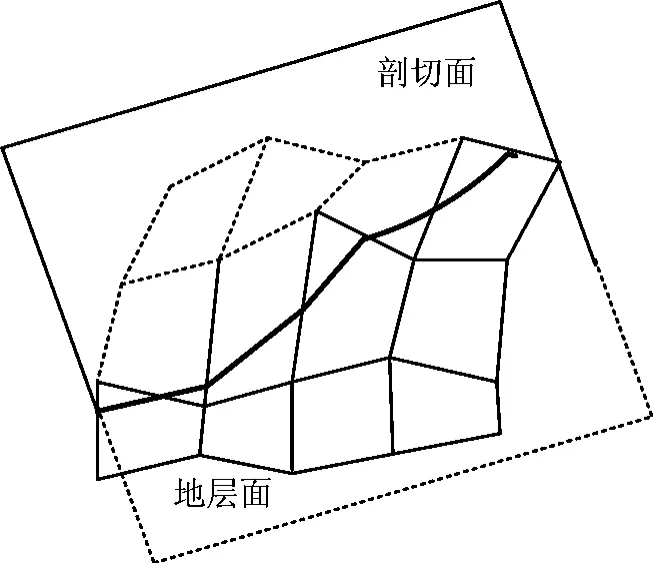
图2 地层面与剖切面交线

设剖切面方程为ax＋by＋cz＋d＝0，某一点M（X，Y，Z）与剖面位置关系可以通过将其坐标值代入剖面方程来判定［10］。设D＝aX＋bY＋cZ＋d，则有：

（1）若D＞0，M点处在平面正法向一侧。

（2）若D＝0，M点处在平面上。

（3）若D＜0，M点处在平面负法向一侧。

检测地层面网格每个三角面片的3个顶点与剖切面的位置关系，若D值均大于0或均小于0，则三角面片与剖切平面不相交；否则，进行求交运算，这时分别对该三角面片的边与剖切平面进行求交判定，若一条边的2个顶点的D值一个大于0而另一个小于0，则由该边的方程与剖切面方程联立求解可得交点P（x，y，z）。

在地层面网格上定义u、v2个方向，并划分为（u－num＋1）×（v－num＋1）的网格，剖切面与地层面交线在水平面上投影如图3所示，图中实线表示剖切面与地层面网格u方向所有平行线相交，虚线表示剖切面与地层面网格u方向部分平行线相交。当u方向平行线与剖切面没有交点时（如u＝u2等），需要将v方向的平行边界线与剖切面的交点（图3中P点）作为u＝u2上交点。具体算法如下。

其次，要注意拓展视听材料的来源。笔者在一学期的教学实践中使用的视听材料大多来自《看视频学英语口语-衣食住行一本通》《悦读联播》《英美文化读本》中的视频、音频材料和英语纪录片，对英语电影和英语歌曲的使用较少。根据问卷结果，学生希望增加英语电影和英语歌曲的内容。因此，在教学内容的选择上应该更多地考虑高中学生年龄特点、学习兴趣和认知水平。

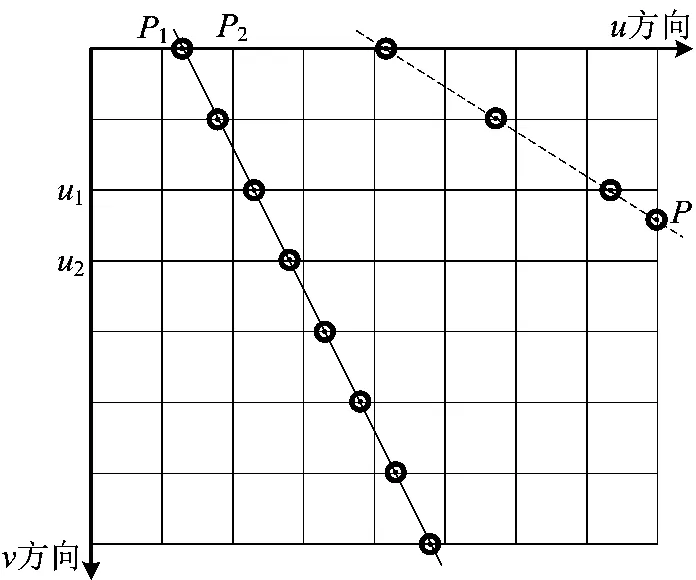
图3 剖切面与地层面交线在水平面上投影

1.1 求地层网格与剖面在u方向的交点

对于地层网格u方向上每一条平行线ui（i＝0，1，…，u－num），取v方向上相邻2点Pui，vj（x1，y1，z1）、Pui，vj＋1（x2，y2，z2），计算D1、D2及它们的乘积Flag。

如果Flag＞0，表明Pui，vj、Pui，vj＋1位于剖切面同侧，需要继续计算下2个相邻点。

如果Flag＜0，表明Pui，vj、Pui，vj＋1点位于剖切面的两侧，可求出线段（Pui，vj，Pui，vj＋1）与剖面的交点P。

如果一条网格线ui上所有点的Flag大于0，表明该网格线与剖切面没有交点，则计算v方向上的边界线与剖切面的交点，即求线段（Pui－1，v－num（x1，y1，z1），Pui，v－num（x2，y2，z2））与剖切面交点，并将此交点作为该网格线的交点Pu。

1.2 确定剖面与地层的剖切情况

计算出了剖切面跟地层面的交点后，还需要考察它在竖直方向上的相交情况。如果剖切面是竖直的，它与各个地层面交点仅高程值不相同（如图4），此时只需要将各个层面对应交点相连成三角形。

如果剖切面是倾斜的，它与各个地层面的交点在水平面上的投影不相同，不仅要计算剖切面与地层面的交点，还要计算剖切面在地层内的交点。当剖切面与某个地层线没有交点时，将其与边界的交点作为地层线交点。如图5中，剖切面与L3层地层线没有交点，将边界线（P1，P2）与地层线的交点P做为L3层地层线交点，而L3以下的地层线不需要再计算交点。计算出所有层内交点后，其剖面的绘制方式与竖直剖面的连接方式相同。

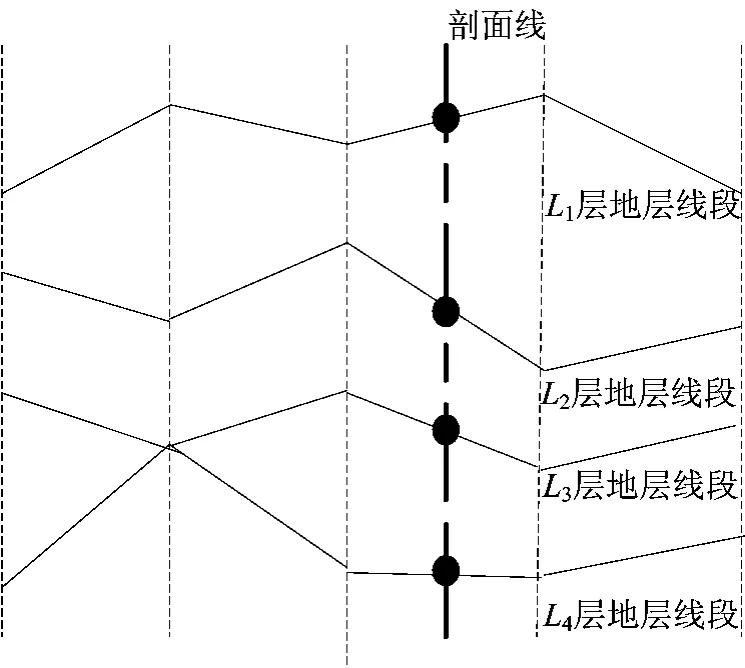
图4 竖直剖切（各层交点仅高程值不同）

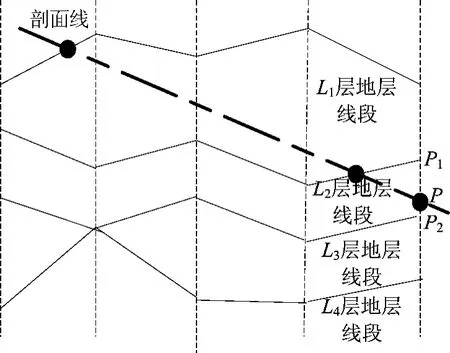
图5 倾斜剖切（贯穿部分地层）

2 基于地层线的三角形渲染

2.1 三角形与地层线的位置关系

当确定了地层面与剖面在各个地层中的交点后，绘制这些交点形成的三角形以及准确对其根据贯穿的地层的颜色进行着色也是进行地质剖切需要解决的问题［10］。具体分析如下：

（2）由于三角形的顶点可能属于不同地层，中间可能跨越其他地层，这需要将三角形按照地层线分割成多个部分，使每个部分只属于1个地层。三角形的3个顶点与地层线的位置关系可能有如下几种：①3个顶点都在同一层，这时不需要进行三角形分割，如图6a所示；②3个顶点分处2层，如图6b所示，这需要将三角形分割成3部分：i层部分、i＋1层至j－1层部分（可能没有）、j层部分；③3个顶点分处于3层，这时地层线与三角形的位置关系如图6c所示，这时需要将三角形分割成5个部分：i层部分、i＋1层至j－1层部分（i、j相邻时没有）、j层部分，j＋1层至k－1层部分（j、k相邻时没有）、k层部分。

（3）在OpenGL中，三角形内部点的颜色值是通过3个顶点的颜色线性插值得到的。但是，对于表示地质体剖切面的三角形来说，其内部各点都应按所属地层的颜色绘制，而不是通过插值计算。这要求将三角形按照地层线分割成多个部分，使每个部分属于同一层。

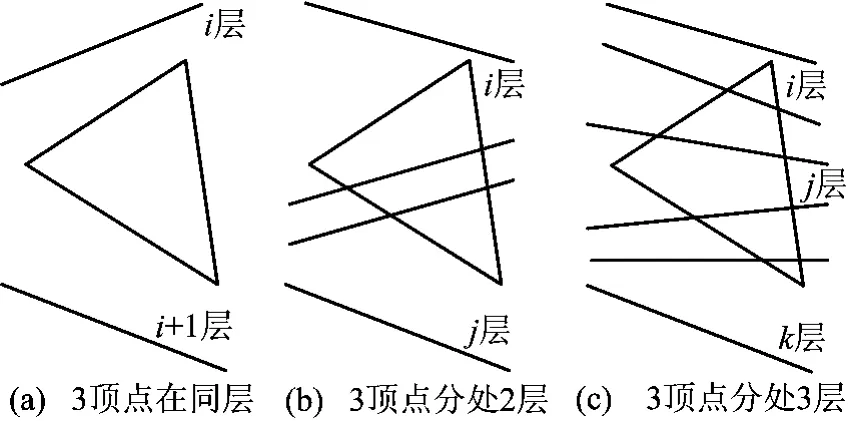
图6 3顶点在地层中位置关系

基于以上考虑，本文提出一种基于地层线的三角形渲染算法。该算法的基本思想是应用扫描线法的基本原理，将地层线做为扫描线对三角形进行分割，利用扫描线与三角形的交点及交点间的地层属性来完成扫描线间的颜色填充。

2.2 三角形分割绘制算法

通过上面的分析可知，如何实现三角形自动分割是需要着力解决的问题。如上所述，三角形最多可能需要分割成5个部分，据此可设计出能够处理各种情况的三角形分割绘制算法。首先将三角形的3个顶点按照所在地层顺序从低到高进行排序，如果遇到2个顶点处在同一层情况，则按照高程大小排序。对于当前三角形，将排好序后的3个顶点分别记为p1、p2、p3，其对应的层号为L1、L2、L3，用flag2和flag3分别表示p2与p3是否已经处理。算法描述如下：

（1）绘制三角形（p1，p2，p3）在L1层的部分。判断（p1，p2）、（p1，p3）是否与L1＋1有交点，若有交点，记为p12、p13，则用L1层地层颜色绘制三角形（p1，p12，p13），如图7a所示；否则，判断（p2，p3）与L1＋1是否有交点，如果（p2，p3）与L1＋1没有交点，即p1、p2、p3在同一层，用L1层地层颜色绘制三角形（p1，p2，p3），转步骤（6），否则，用L1层颜色绘制2个三角形（p1，p2，p23），（p1，p23，p13），flag1＝true（如图7b所示），转步骤（4）。

（2）绘制L1＋1到L2之间部分。对于L1＋1到L2之间各层L，求出（p1，p2）与L层、L1＋1层的交点p12、p12′，以及（p1，p3）与L层、L1＋1层的交点p13、p13′，用L层地层颜色绘制2个三角形（p12，p12′，p13）、（p13，p12′，p13′）。

（3）绘制三角形（p1，p2，p3）在L2层的部分。求出（p1，p2）与（p1，p3）与L2层之间的交点p12、p13，判断（p2，p3）、（p1，p3）是否与L2＋1有交点：若都存在交点p23、p13′，则用L2层颜色绘制3个三角形（p12，p2，p23）、（p12，p23，p13）、（p13，p23，p13′），如图8a所示；否则，用L2层颜色绘制2个三角形（p12，p2，p3）、（p12，p3，p13），如图8b所示，转步骤（6）。

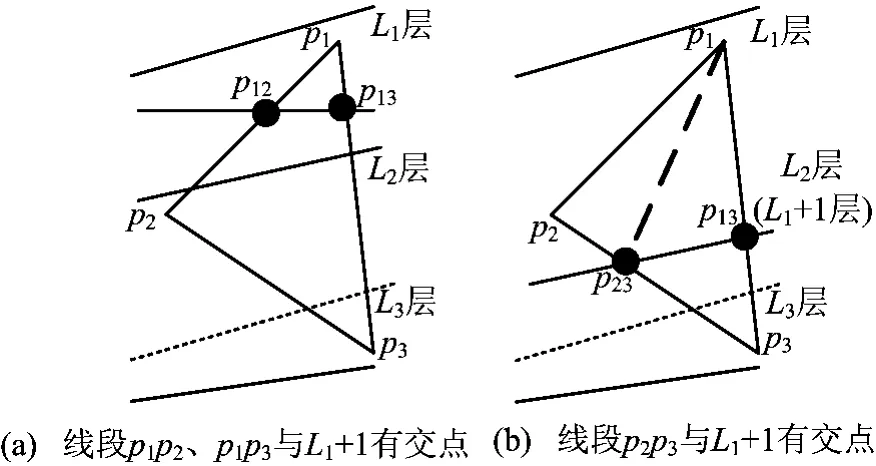
图7 绘制三角形（p1，p2，p3）在L1 层的部分

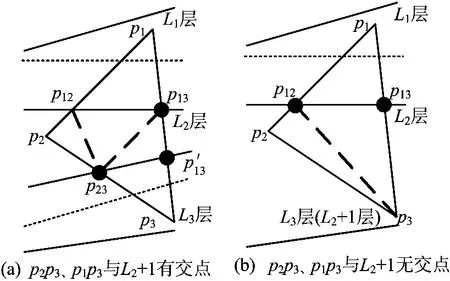
图8 绘制三角形（p1，p2，p3）在L2 层的部分

（4）绘制L2＋1到L3之间部分。对于L2＋1到L3之间各层L，求出（p2，p3）与L层、L1＋1层的交点p23、p23′，以及（p1、p3）与L层、L1＋1层的交点p13、p13′，用L层地层颜色绘制三角形（p23，p23′，p13′）、（p23，p13′，p13）。

（5）绘制L3层的点。求出（p1，p3）、（p2，p3）与L3的交点p13、p23，用L3层地层颜色绘制三角形（p23，p3，p13），如图9所示。

（6）结束。图7～图9中，点虚线表示可能存在的地层，粗虚线表示将多边形分解成三角形的分界线。

图9 绘制L3层的点

3 实验结果

在PC机上，采用Visual C＋＋和OpenGL编程，对上述算法进行了实现，并应用该算法对某区工程地质模型进行了三维剖切。该区域共收集10个钻孔，包含8个地层，经数据处理后10个钻孔的局部位置坐标和每个钻孔贯穿各个地层面高程数据见表1、表2所列。以表中10个钻孔点为离散点，运用空间插值以及由曲面拟合得到的各地质结构趋势面，获得地质体的三棱柱结构模型，然后运用可视化算法，对该模型进行处理，绘制出具有真实感的三维地质结构图，如图10、图11所示。为了更好地了解地质内部地质结构，对地质体结构进行三维剖切，图12、图13分别为竖直剖切后的剖切面结构和剖面分离地质体的结果图，图14所示为贯穿所有地层的倾斜剖切面产生的剖切图。图15所示为贯穿部分地层的倾斜剖切面产生的剖切图。

表1 10个钻孔的局部位置坐标

表2 钻孔贯穿各个地层面高程数据

图10 地质体三棱柱网格

图13 竖直剖切

图11 三维地质结构图

图12 剖面图

图14 贯穿所有地层的倾斜剖切

图15 贯穿部分地层的倾斜剖切

4 结束语

采用三棱柱建模方法构造了真实感的三维地层模型，并应用三维空间求交算法和基于地层线的三角形绘制算法，可由任意切面对三维地质模型进行剖切，得到三维的剖切实体图、切面图，使不熟悉地质结构和构造复杂性的人对地质空间关系有一个直观的认识，并提高对难以想象的复杂地质条件的理解和判别，对实际的工程地质分析和解释具有指导意义，可以很好地满足层状地质结构实际应用的需要。该算法对地层相互穿插、出现断层等复杂地质结构的三维剖切效果较差，且未考虑复杂地质构造（如侵入体、复杂褶皱等）的影响与作用，因此仍需随着实际应用的深入而作进一步研究。

［1］刘 喜.三维地质建模关键算法研究［D］.合肥：中国科学技术大学，2011.

［2］朱良峰，潘 信，吴信才.地质断层三维可视化模型的构建方法与实现技术［J］.软件学报，2008，19（8）：2004－2017.

［3］李 楠，曾俊钢，肖克炎，等.一种线框矢量模型表示的地质体折面剖切方法［J］.测绘科学；2011，36（6）：28－31.

［4］梁师俊.基于虚拟钻孔的工程地质三维剖切的实现［J］.地理与地理信息科学，2010，26（1）：11－14.

［5］郭加树，张 勇，毕世普，等.一种三维地层模型可视化及剖切分析方法［J］.海洋地质动态，2010，26（11）：51－54.

［6］邹 伟.三维地质勘查软件核心技术研究与实现［D］.北京：中国地质科学院，2010.

［7］De Ricazo F，Oreste P，Pelizza S.Subsurface geologicalgeotecbnical modelling to sustain underground civil planning［J］.Engineering Geology，2008，96（1）：187－204.

［8］Smirnoff A，Boisvert E，Paradis S J.Support vector machine for 3Dmodelling from sparse geological information of various origins［J］.Computers ＆ Geosciences，2008，34（2）：127－143.

［9］黄地龙，邓 飞.复杂地层结构模型三维重构与可视化方法研究［J］.成都理工大学学报，2008，35（5）：553－558.

［10］陈国良，曹卫群，黄心渊.一种由等高线模型生成规则格网模型 的 算 法 ［J］.中 国 图 象 图 形 学 报，2007，12（6）：1110－1113.

3D sectioning algorithm of geology based on stratum line

HUANG Zhong1，2， JIANG Ju－lang1， ZHANG You－sheng2

（1.School of Physics and Electronic Engineering，Anqing Normal University，Anqing 246011，China；2.School of Computer and Information，Hefei University of Technology，Hefei 230009，China）

Three－prism structure model of engineering geology is built by taking geological drillings as discrete points and applying each trend surface of geological structures，which are calculated by the spatial interpolation and surface fitting algorithm.On this basis，a sectioning method of arbitrary cutting is proposed.First the 3Dspace intersection algorithm is used to quickly calculate the intersections of cutting plane and rugged trend surface，and then in terms of stratigraphic sequence these intersections create triangles，which are colored accurately according to cross－cutting strata properties.As a result，the entity diagram and section diagram of 3Dcutting are obtained，which can give new means for geologists when they observe geological structures and analyze geological features in 3Dspace，thus providing a scientific basis for the decision－making of the design，management and construction of geological projects.

trend surface of geological structure；space intersection；section plane；inclined cutting；sectioning analysis

TP391.41

A

1003－5060（2013）02－0202－06

10.3969／j.issn.1003－5060.2013.02.016

2012－09－21；

2012－10－31

国家自然科学基金资助项目（60575023）；安徽省自然科学基金资助项目（090412065）和安庆师范学院青年科研基金资助项目（KJ201007）

黄 忠（1981－），男，安徽安庆人，安庆师范学院讲师，合肥工业大学博士生；

江巨浪（1966－），男，安徽安庆人，博士，安庆师范学院教授；

张佑生（1941－），男，湖南浏阳人，合肥工业大学教授，博士生导师.

（责任编辑 马国锋）