LLC谐振变换器的谐振元件设计
柏 余,王 荣,朱忠尼,王永攀
(1.空军预警学院 研究生管理大队,湖北 武汉430019;2.空军预警学院 五系,湖北 武汉430019)
0 引 言
随着电源高频化技术的发展,在中小功率场合及分布式电源系统中,谐振变换器由于工作频率高,容易实现软开关等优势日益受到重视。在LED灯电源、高压气体放电灯等领域得到了广泛应用[1,2]。
根据拓扑结构来划分,谐振变换器目前主要有:串联谐振(SRC)、并联谐振(PRC)、串并联谐振(SPRC)及不对称半桥谐振变换器(AHB)等传统变换器[3]。这些变换器可以有效实现开关器件的零压、零流开通和关断,但存在电压增益非线性变化、副边整流二极管电压电流应力大、变换器工作频率fs只能大于谐振频率fr,造成轻载工作频率太高等问题。
为了解决上述问题,相继出现了LCC,LLC,LCLT等多种拓扑结构,其中,LLC由于具有:(1)fs可以小于fr;(2)原、副边器件均为零压开通和零流关断;(3)电路结构简单,效率高;(4)输入电压范围、输出功率范围大;(5)原、副边开关器件电压应力低;(6)针对负载变化,频率调节范围小等优点,使其具有很高的研究和应用价值[4]。
近年来,人们对LLC谐振变换器的理论已经有了深入的研究,在这些理论基础上,本文重点研究了谐振元件中的参数设计,给出了电感元件的磁芯选择方法、绕组计算等。
1 LLC变换器的拓扑结构及谐振参数设计要求
1.1 拓扑结构及工作原理
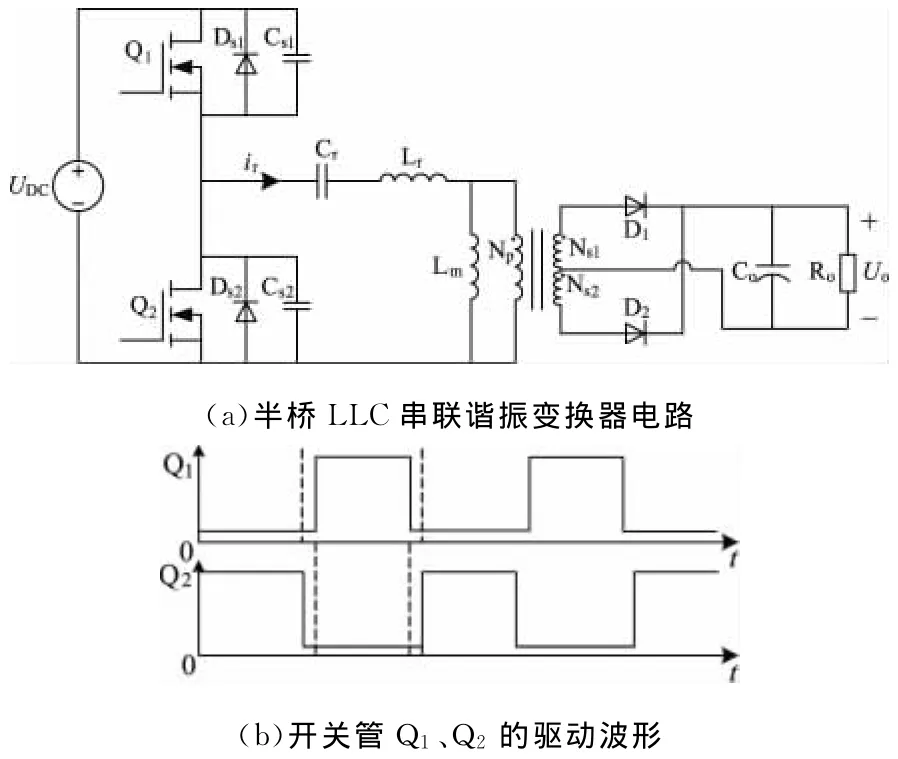
图1 半桥LLC串联谐振变换器拓扑及工作波形
图1(a)所示的变换器包含三个部分:方波产生、谐振部分和次级整流。直流电压通过交替导通的开关管Q1和Q2来产生方波;谐振电容Cr、谐振电感Lr和励磁电感Lm共同组成变换器的谐振部分;次级整流主要是通过带中心抽头的变压器和二极管D1、D2以及输出电容Co来完成的。其工作原理文献[5]~[7]都有详细介绍,本文不再赘述。
1.2 谐振参数的约束条件
(1)Lr,Lm约束条件
根据文献[8]介绍,LLC变换器的增益
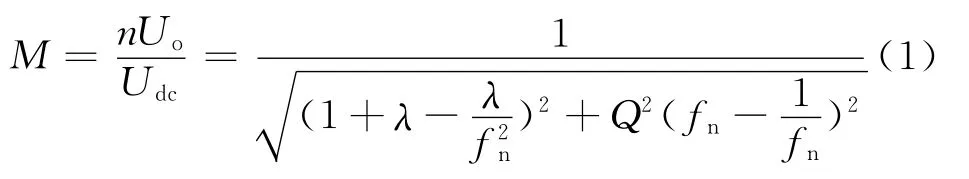
式中,Uo为输出电压;n是变压器匝比,且n=;λ是电感比;;fn为频率归一化表达式,;f s为开关频率;fr为谐振频率,fr=;Q为电路品质因数,Q=。
根据式(1),满足M>0及电路能安全工作的条件要求:
①工作频率fs可以在频率fm<fs<fr及fs>fr范围内工作,其中fm=。
②当fs=fm时,LLC整个槽路串联谐振引起功率开关管短路,为此,要求

③开关管Q1(Q2)能实现零电压开通(ZVS)的条件是Lm中存储的能量在开关器件死区期间完成对C1(C2)的充放电,即励磁电流的峰值ILm不能太小。文献[5]中规定:

(2)对Q 的限制
图2是LLC谐振变换器工作等效电路。图中,Roac是负载的交流等效阻抗。
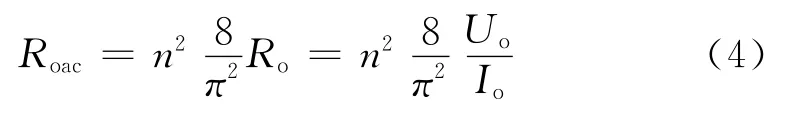

图2 LLC谐振变换器工作等效电路
根据图2,得到输入阻抗为:

将式(5)写成频率归一比表达式:

根据前面的分析,电路工作时,Zin(jw)应为感性,所以有:

当Ro等于额定负载时,Q=Qmax,fn=fnmin,M=Mmax,对式(1)求导得到:

将式(8)代入式(7)得到:
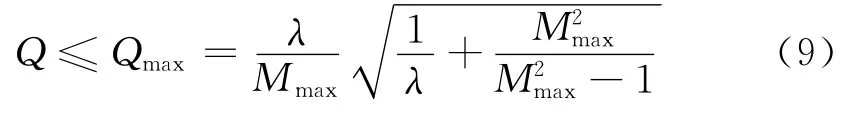
在设计中,为避免过大的谐振电流,一般要求:

(3)谐振元件的参数计算公式
设Ro=RN时,fs=fr,即fn=1时,

得到:
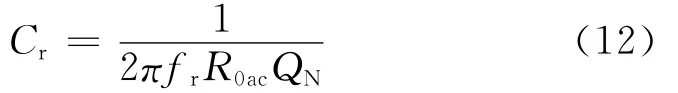
根据式(12)计算出的参数及图2的等效电路充放电原理,可以得到谐振电容最大电压应力为:
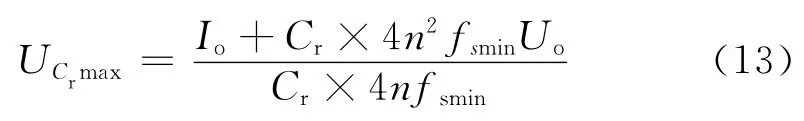
根据谐振频率公式及λ=Lr/Lm得到:

电感气隙与电感量、匝数的关系为:
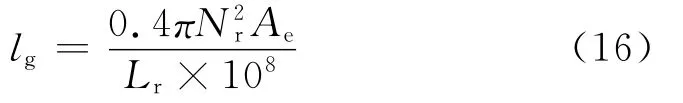
2 谐振电路磁性元件的设计
2.1 谐振电感Lr的设计
Lr的参数由式(14)给出,下面计算流过谐振电感Lr的电流。
(1)谐振电流
流过电感电流由两部分组成,一是通过变压器耦合到负载的电流();二是励磁电流im。与I相m位相差90°,所以,谐振电流的峰值为:

式(17)中含励磁电流峰值:

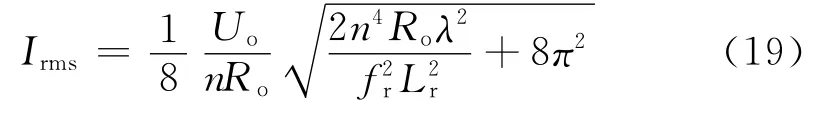
(2)谐振电感Lr铁芯选择
交流电感铁芯的选择主要是依据电感的储能,储能表达式为:

功率容量为:

2.2 变压器的设计
上面的分析说明LLC变换器输出变压器与普通开关电源变换器有很大的不同,其主要表现在:它需要先确定励磁电感Lm的值,由于Lm=较小,其励磁电流较大,容易引起变压器初级饱和。因此,铁芯选择按如下步骤进行。
(1)根据功率确定面积乘积[9]
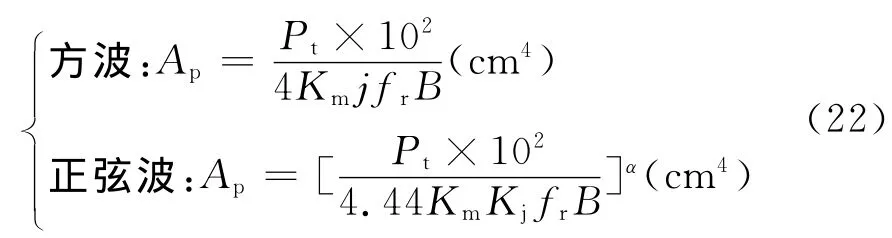
式中,Km为线圈占空比;j和Kj都为电流密度;B为磁感应强度;Km取0.3;j取4 A/mm2;Kj取3.66A/mm2;B 取150 mT。
Pt是变压器计算功率,输出全波整流时,
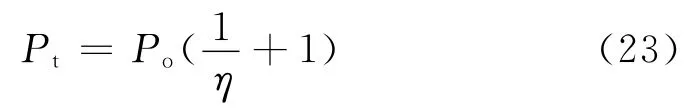
式中,η为效率。
(2)根据Lm确定变压器匝数
LLC变换器输出变压器的初级匝数不能采取常见公式

计算。而是通过电感量的计算公式(安培环路定理)确定N、Ae和le,通过变压器电路分析得到LLC变换器设计公式为:

式中,μe为有效导磁率;le为磁路系数(cm);Ae为磁芯截面积(cm2);μe、le、Ae均可从磁性材料手册中查出。
3 设计实例
3.1 主要技术指标
输入电压Uin:400 V(DC)(经PFC预稳压);输出功率Po:500 W;谐振频率fr:40 kHz;拓扑结构如图1所示的半桥LLC变换器;输出电压Uo:48 V。
3.2 谐振电路参数
(1)有关参数选择
选取:Mmax=1.2,λ=0.25,=4.1(U为整流二d极管压降)=4.6(Ω)。
由式(4)得到输入交流阻抗:

由式(8)得到:

满足要求。
由式(9)得到:

(2)谐振元件参数计算
由式(12)得到谐振电容取Cr=120 nF。
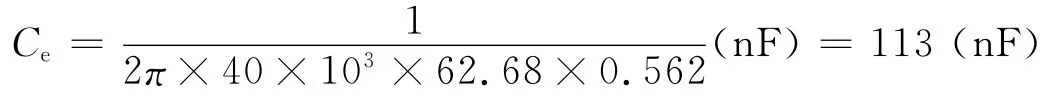
由式(13)得到谐振电容电压应力为:

选4只30 nF CBB/600 V薄膜电容并联。
根据式(14)、(15)得到:
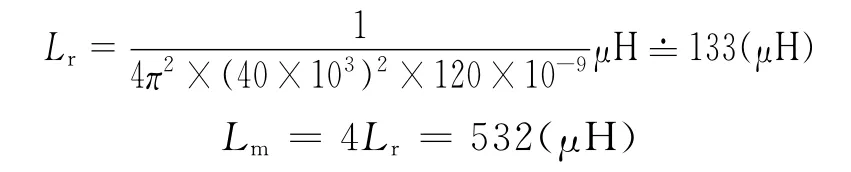
(3)谐振电感的设计
由式(17)、(18)、(19)得到流过谐振电感的峰值电流和有效值电流分别为:

由式(20)、(21)得到电感的功率容量为:

由于流过Lr的电流为正弦波,按式(22),选择EE型磁芯,则α=1.14,有:
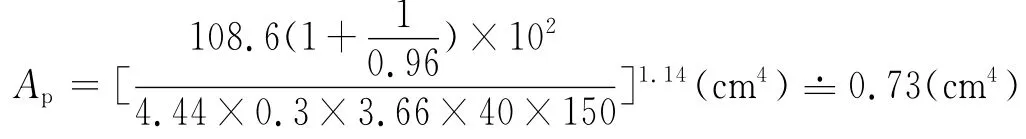
查表选择EE30×30×7 mm3铁氧体磁芯,磁芯的基本有效参数为:le=65.9 cm,Ae=58.2 mm2。用φ=0.44 mm漆包线5股并绕,给定气隙lg=0.5 mm,则电感匝数可由式(16)得到:
Nr==30.16(匝),取Nr=30匝
(4)变压器设计
设次级全波整流,效率η2=0.92,而且流过变压器的为方波,由式(22)得到变压器面积乘积:
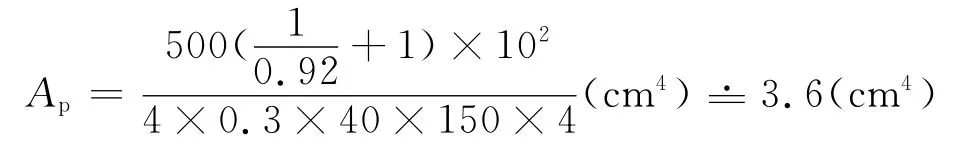
查表选择EE60×72×15.6 Mn-Zn铁氧体磁芯。该铁芯的基本参数:Ap=19.8 cm4,Ae=2.4 cm2,le=16.6 cm,μe=1 800。根据式(25)求得初级匝数:

取N1=25匝,次级N2=6匝。
N1的匝数小于采取公式(24)设计的匝数(75匝),在该参数下:
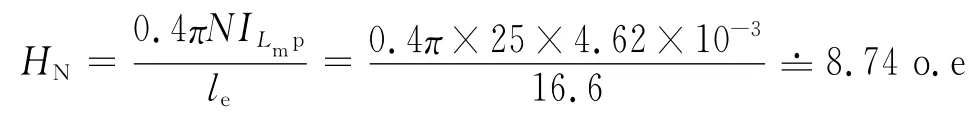
查 Mn-Zn铁氧体B-H 曲线,HN=8.74o.e时,对应的Bm在0.2T~0.3T之间,小于Bs(Bs=0.5 T),变压器不会饱和,满足设计要求。
4 实验结果及分析
图3是根据上述参数制作的一台LLC谐振变换器的实验波形。
图3(a)是开关管Q1(Q2)上的电压波形及驱动电压波形,由图可以看出,开关管实现了零压开通(ZVS)。
图3(b)整流二极管D1(D2)上的电流波形及驱动电压波形,由图可以看出,实现了零电流关断(ZCS)。
图3(c)是fs=0.6fr带额定负载时驱动信号与Ur的波形。根据式(1)可以得到M=1.3。
图3(d)是fs=fr带额定负载时驱动信号与Ur波形。由式(1)可以得到M=1,电路全谐振。

图3 试验电路部分波形
5 结 论
本文从分析LLC谐振变换器的特性出发,给出了谐振元件的约束条件,在此基础上,进行了谐振元件的详细分析计算及参数设计,包括变压器部分参数的计算和设计方法,并根据设计理论研制了试验样机,得到了试验波形。试验结果证明对LLC谐振变换器谐振元件和变压器的参数设计方法是正确的。
[1] 张久庆.基于LLC谐振的LED驱动电源设计[J].电力电子技术,2012,46(3):9-11.
[2] 梁国辉.基于LLC谐振的多路输出LED路灯恒流驱动电路[J].微电子学,2011,41(5):668-671.
[3] YANG B.Topology investigation of front end DC/DC converter for distributed power system[D].Virginia:Virginia Polytechnic Institute and State University,2003.
[4] 朱姝姝.宽电压输入半桥型LLC谐振变换器设计与实验[J].电力电子技术,2012,46(3):65-67.
[5] 庞里生.全负载范围高效率LED路灯驱动电源研究[D].广州:华南理工大学,2010.
[6] 杨益平.谐振DC/DC变换器研究[D].杭州:浙江大学,2005.
[7] 张振银.200 WLED驱动电源研究[D].成都:电子科技大学,2011.
[8] 于平义.高功率LLC谐振变换器的设计方法[J].计算机仿真,2011,28(9):327-349.
[9] 王保全.新编电子变压器手册[M].沈阳:辽宁科学技术出版社,2007.
[10]宫 力.LLC串联谐振全桥DC/DC变换器的研究[D].武汉:华中科技大学,2006.
[11]赵敏杰.LLC谐振变换器的参数设计[J].磁性材料及器件,2011,42(2):53-57.

