一种简化SVPWM算法仿真及其FPGA实现
姜学岭,常柯阳
(华北电网冀北电力公司承德供电分公司,河北 承德067400)
0 引 言
SVPWM算法因其较高的直流电压利用率和易于数字电路实现的优点,在变频电源、电机控制等多种场合下得到广泛的应用。但传统的SVPWM算法比较复杂[1,2],包含坐标转换、扇区判断、基本矢量作用时间及开关时间计算、饱和处理及PWM脉冲输出。通常要用到四则运算或者是求根运算。本文根据SVPWM算法比较原理,采用了基于调制函数的算法[3],直接计算三相调制函数,避免了求根和除法等运算,能够方便地在数字系统实现。
文中给出了算法的Matlab/Simulink环境下搭建的模型,将其运用在电机控制开环系统中,进行了仿真,验证了算法的正确性。并将算法在FPGA芯片上实现,突出了算法易于数字化实现的特点,完成了软件仿真和硬件测试。
1 基于调制函数的SVPWM算法的原理
典型的SVPWM算法的原理在文献[1,2]中已经给出了详细的描述,其实质是一种对在三相正弦波中注入了零序分量的隐含调制波(鞍形波)进行规则采样的变型SPWM[4,5]。而基 于调制 函数的SVPWM 算法[3]就是要通过简单的计算得到三相调制波的调制函数和每相电压在一个PWM周期中的占空比。
图1显示了扇区划分方式,判断参考电压矢量Ur位于哪个扇区时,需按公式(1)先计算其在xyz三相系下的分量。为计算方便,这里将对参考矢量做标么化处理,以其最大值作为标准值,这样可将公式(1)简化为式(2)。


则Ur所在扇区编号为

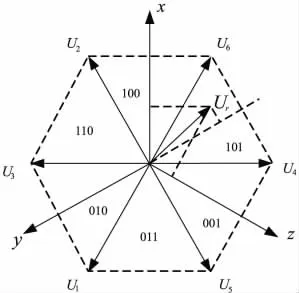
图1 扇区划分
各扇区参考矢量的调制函数如式(4)~(6)所示。式(4)为101、010扇区的计算公式:

式(5)为100、011扇区的计算公式:

式(6)为110、001扇区的计算公式:
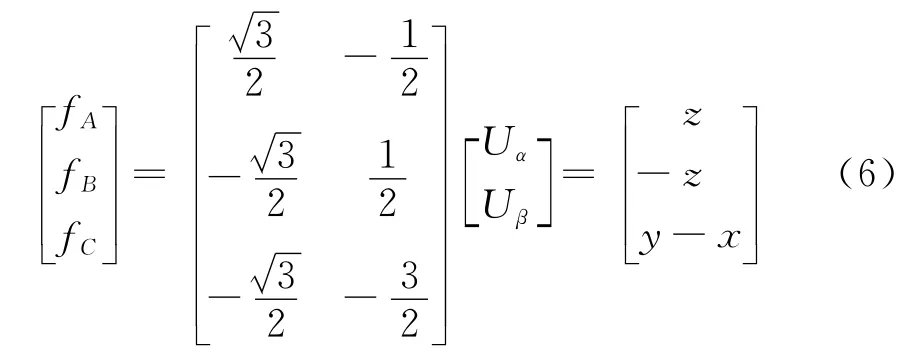
对参考电压矢量过饱和的处理,仅需令调制函数满足
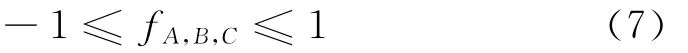
上述算法,在扇区判断与调制函数计算时,只需计算出三个变量x、y、z,和三个变量的加减运算即可,与传统算法相比,计算量减少了将近一半;在做饱和处理时,只需做限幅约束即可,而传统算法要依据式(8)
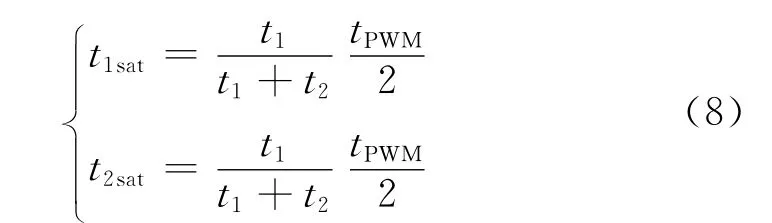
计算,相比省去了复杂的除法。
图2中SVPWM模块为本算法在 Matlab/Simulink下的仿真模型,给模块输入三相交流信号Ia、Ib、Ic,输出PWM脉冲经逆变器接PMSM电机模型。图3中给出了仿真结果,其中(a)显示的是调制函数fA、fB、fC的波形;图(b)是输出PWM脉冲接滤波函数滤波后的波形;图(c)是电机输出的三相电流波形。
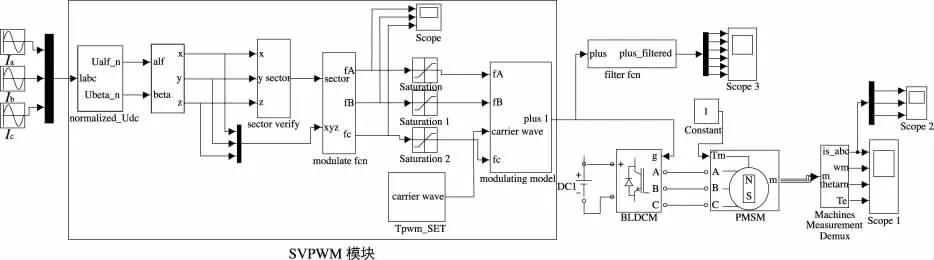
图2 基于调制函数的SVPWM算法及其在电机开环系统中的仿真模型
2 基于调制函数的SVPWM算法的FPGA实现
由图4可知,本算法实现由中间变量模块、扇区判断模块、调制函数计算模块、三角载波生成模块、比较单元、死区生成模块组成。整个设计过程是在QuartusⅡ7.2环境下实现,采用VHDL语言与.bdf原理图编写,各数据量均采用定点Q值格式,系统时钟频率设置为50 MHz。
2.1 中间变量模块和扇区判断模块
在这里,设定输入变量Uα、Uβ为经过标么化处理后的值,故其范围为[-1~1],采用16位1Q14格式。由式(2)知,中间变量x、y、z绝对值的最大值为+1,在1Q14格式表示范围内。将用多个2-n的和来逼近,≈1+2-1+2-2-2-5,而2-n可以用移位运算实现。这样,整个运算就移位和加减法即可。省去了复杂的乘法和除法运算。
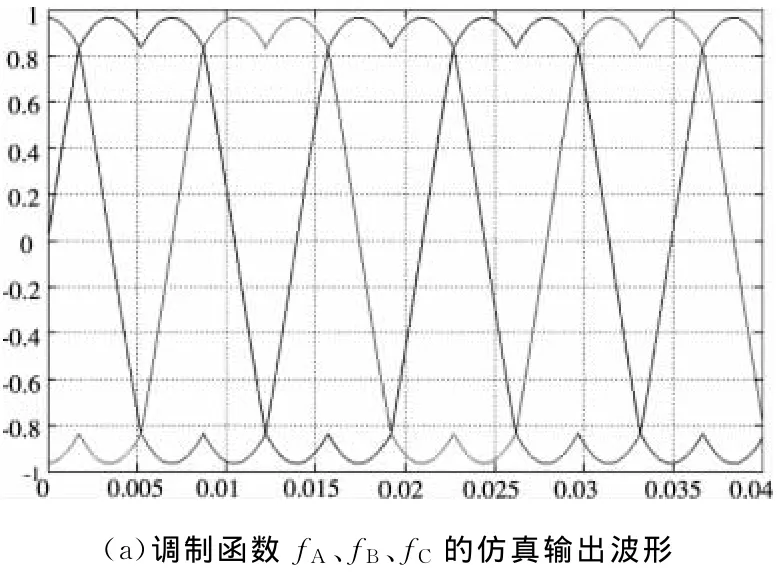
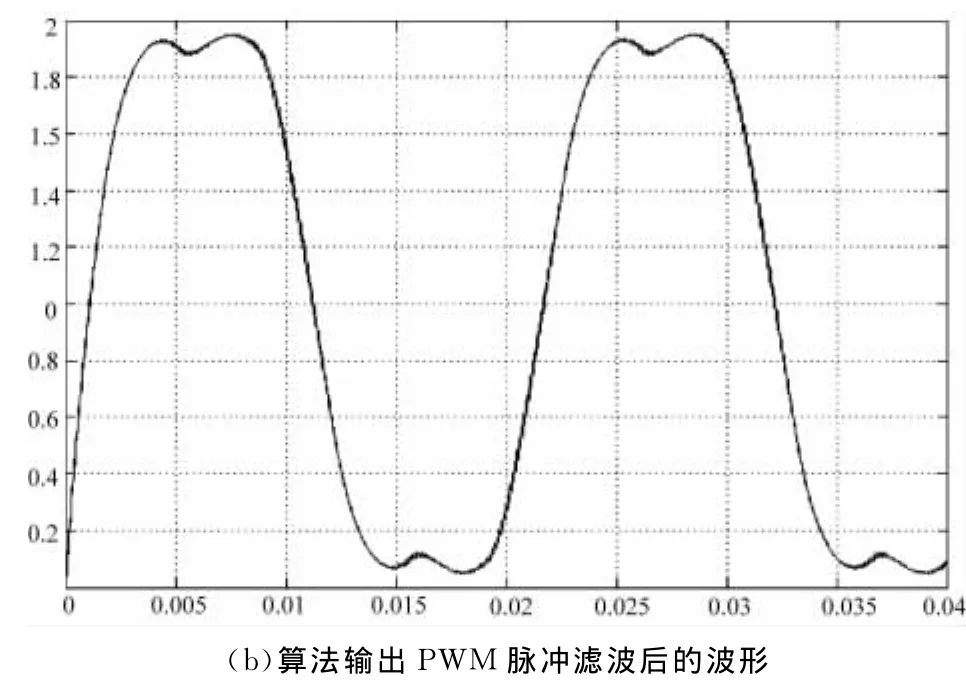

图3 基于调制函数的SVPWM算法的仿真结果
在进行扇区判断时,由于数据均采用有符号的格式,所以,数据首位即可反映出其正负性。因此,按照式(3),用VHDL编写扇区 K≤not(X(wth-1))&not(Y(wth-1))&not(Z(wth-1))。
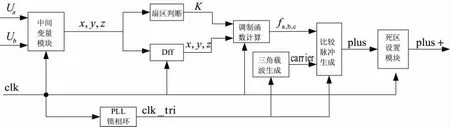
图4 算法的FPGA实现框图
2.2 调制函数计算模块
根据式(4)~(6),利用加减法即可得;然后根据式(7)进行限幅处理。
2.3 三角载波生成模块
三角波的周期T为逆变器件的开关周期;幅值范围为[-1~1];利用片内PLL对系统时钟进行倍频,得到频率为160 MHz的clk_tri作为本模块的时钟。这里,采用米立型(Mealy)状态机实现,如图5中所示,定义三角波上升状态为S0,下降状态为S1,加减计数器的计数值为tri(数据采用Q11格式),周期结束信号为t_done。模块实现逻辑如表1所示,其中current state和tri(n)为当前状态和数据;next state和tri(n+1)、t_done是下一状态和输出值。
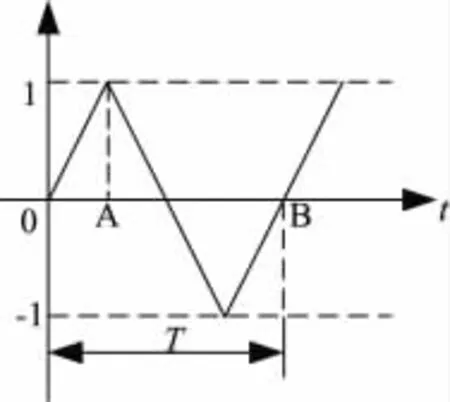
图5 三角载波波形
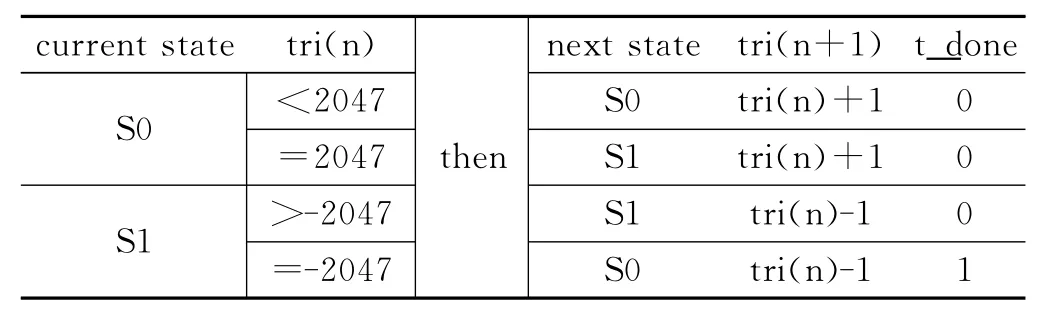
表1 三角载波生成模块实现逻辑
2.4 比较单元
模块功能主要是对三角载波tri和调制函数fA、fB、fC进行比较,从而根据式(9)输出PWM脉冲。

当每一个三角波周期结束时,即到达图5中的B点时,三角载波生成模块就会产生一个脉冲信号t_done,将此信号作为比较单元的使能信号,在其上升沿到来时,将本周期的调制函数fA、fB、fC载入比较单元。
2.5 死区模块
模块功能:为防止同一桥臂的两个开关管同时导通,应先关断其中一个之后再打开另外一个。
这里利用计数器来实现死区时间。本设计中设定死区时间为4μs;由图4知,模块时钟clk的频率为50 MHz,从而可得死区计时器的计数上限为200。
将以上各功能模块连接,即可得到如图6所示的SVPWM算法的设计图。
3 仿真及实验结果

图7 设计仿真结果
在QuartusⅡ7.2开发环境下对上述设计文件进行综合仿真,并下载至芯片进行板级仿真,用signal tap测得输出PWM波形如图7所示。
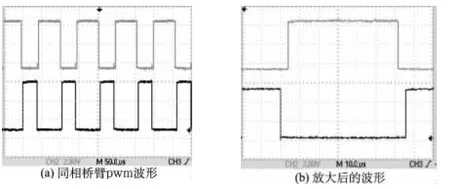
图8 输出PWM波形
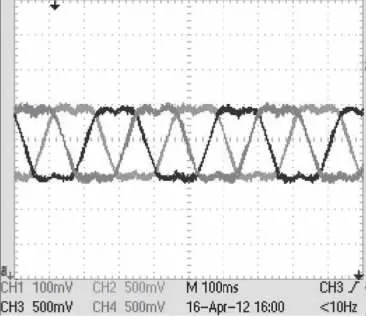
图9 低通滤波后的PWM波形
用示波器对输出波形进行观察,可得到图8和图9。其中,图8(a)为同一相上下桥臂的PWM波形,图8(b)为放大后的波形,可清楚的看到上下桥臂的死区设置;图9为三相PWM波经过阻容滤波后得到的马鞍波。
4 结 论
本文依据基于调制函数的SVPWM算法理论,给出了算法实现的框图,在Matlab/Simulink环境下进行了建模和仿真,并将算法在FPGA上实现,通过仿真和硬件测试结果验证了算法的正确性,同时也说明了该算法非常易于数字化实现,适合在工程实际中采用。
[1] 陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2009.
[2] 曾 聪,刘涤尘.空间矢量脉宽调制技术的算法及其仿真研究[J].电力科学与工程,2009,25(8):5-9.
[3] 陆海峰,瞿文龙,张 磊,等.基于调制函数的SVPWM算[J].电工技术学报,2008,23(2):37-43.
[4] 文小玲,尹项根,张 哲.三相逆变器统一空间矢量PWM 实现方法[J].电工技术学报,2009,(10):87-93.
[5] 周卫平,吴正国,唐劲松,等.SVPWM的等效算法及SVPWM与SPWM的本质联系[J].中国电机工程学报,2006,26(2):133-137.

