逼近于的递推数列的构造

刘国祥

（赤峰学院数学与统计学院，内蒙古赤峰024000）

刘国祥

（赤峰学院数学与统计学院，内蒙古赤峰024000）

用两个自然数之比近似地代替一个无理数，或者用两个有理数之比逼近于一个无理数，是数学学科一个古老的问题.人们已经得到许多有效的方法.本文讨论构造递推数列，使得通项之比逼近于无理数（N是非平方自然数）.

斐波那契数列；递推数列；佩尔方程

用两个自然数之比近似地代替一个无理数，或者用两个有理数之比逼近于一个无理数，是数学学科一个古老的问题.典型的例子是圆周率π的近似表示.人们已经得到许多有效的方法，如连分数等.本文讨论构造递推数列，使得同项之比逼近于无理数（.N是非平方自然数）.

1 用斐波那契数列逼近于

斐波那契数列由递推格式定义：

它的前几项分别为：1，1，2，3，5，8，13，21，34，55，89

它的通项公式为熟知的：

他有许多优美的性质，其中之一是：

对（3）进行适当地变形就有：

显然bn∈N，并且有：

看一下这些数的规律，记分母的数列为an，它的项是1，2，5，12，29，70，……

则数列可以用递推形式给出：

从（10）中消去bn，有：

设存在实数x,y，使得等比数列{an+1+x an}以y为公比，则：

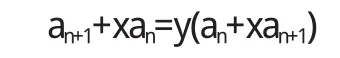
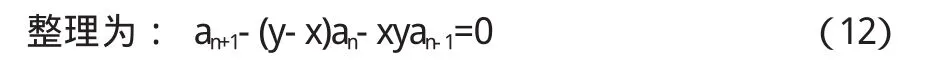
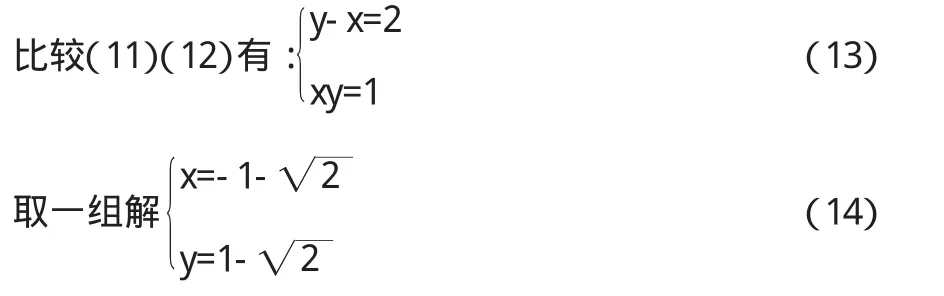
于是有：

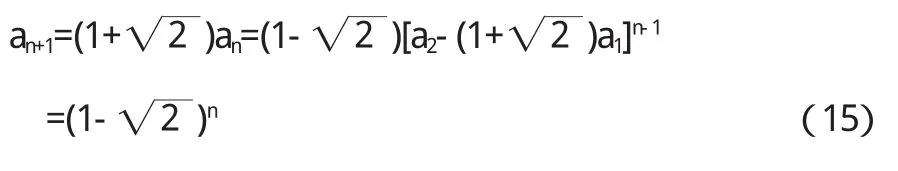
考虑到an+1-an=bn，

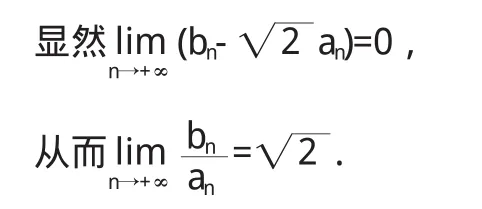
3.1 通项公式

考查（13）的另一组解：

应用上述同样的方法得到与（16）类似的式子：

如果把上述讨论的2变为其他的非平方自然数N,如3，5，6，7，8，10，11等.

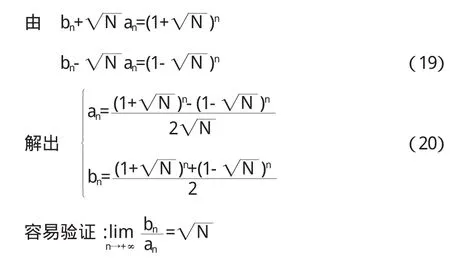
3.2 递推公式

用通项公式（20）计算an,bn比较困难，认真观察（19）和（20）并且与（10）比较，不难发现可以用递推公式给出：

显然（10）是(21)的N=2的特例.（20）是（21）的显式通项形式.

3.3 初值a1,b1的选取

在（21）中，取a1=b1=1当然简单，但不是必要的.

如果取a1=s,b1=t,s,t∈N

显然（21）是（24）在s=t=1时的特例.（23）是（24）的显式通项形式.

3.4 与双曲线的关系

从（20）中可以得到：

另外，从（26）明显看出与佩尔方程的关系，现不详细讨论.

〔1〕M.克莱因.数学：确定性的丧失[M].长沙：湖南科技出版社，2001.

〔2〕卡尔文.C.克劳森.漫游数学王国[M].上海：上海教育出版社，2001.

〔3〕沈康身.历史数学名题赏析[M].上海：上海教育出版社，2002.

O151

A

1673-260X（2013）03-0001-02