上证指数不同时间周期收益率正态分布性分析

薛灵芸

中央财经大学保险学院，北京 102206

引言

现代金融理论最重要的理论基础是有效市场假说(Efficient Market Hypothesis，简称EMH)。在20世纪初Louis Bachelier提出可以用布朗运动来描述股价波动，首开有效市场假说研究先河。1964年Osborne提出股票价格的变动有如流体中的粒子，遵循布朗运动。Osborne认为投资者能够充分利用所有已知信息，股票交易在价值与市场价格一致的均衡价格上进行。由于股票价格是在已知的信息下的均衡价格，价格的变动在时间序列上也就相互独立，上期的价格对下一期的价格没有直接的影响。由概率论中的中心极限定理可以进一步推论，股票价格服从正态分布，具有稳定的均值和有限的方差。

1965年Samuelson提出信息有效市场概念，用经济学理论论证有效市场假说。Roberts根据市场对信息集的不同反映，将股票市场分为弱式有效市场（价格仅反映历史价格信息）、半强式有效市场（价格反映所有公开信息）、强式有效市场（价格反映所有能获得的信息）。1965年法玛（Fama）总结了有效市场理论，正式提出有效市场假说。Fama对有效市场的定义是：在一个有效的市场中，证券价格总是能充分地反映所有已知的信息。1970年Fama认为，有效市场假说使得所有基于现有信息之上的交易策略不可能获得超过市场平均利润。众所周知的马柯维茨的资产组合理论、Willian Sharpe(1964)的资本资产价模型(CAPM)、布莱克-斯科尔斯的期权定价模型都是以有效市场假说为基础。有效市场假设理论假定金融资产的价格收益率分布服从正态分布，并有稳定的均值和有限的方差。

金融资产的收益率分布特性对各种金融模型的正确性具有决定性影响，国内外很多学者对收益率的分布特性做了大量实证研究。实证研究表明，价格波动的布朗运动模型和有效市场假说并不能完美近似市场。由于投资者的认知能力不同、市场非理性的广泛存在，金融市场的非理性广泛存在，导致收益率的分布表现为相比正态分布具有尖峰厚尾性。German(1978),Lau&Wingender(1990)等学者相继发现，股票收益率的分布往往具有如下特征:

(1)有偏性。偏度往往大于0，即概率分布不是对称的；

(2)尖峰厚尾性。峰度系数往往要远大于0，也就是说，收益率剧烈波动，出现极端离群值的概率要远大于理论正态分布假设下极端事件发生的概率。

上海股市自1990年开市以来，已经有23年的历史。由于上海股市的历史不长，属于新兴市场，波动性与成熟股市有差异，其收益率的分布特性自然与成熟股市也不同。本文在前人研究的基础上，尝试对市场收益率的不同时间周期数据进行对比分析，以图揭示不同时间周期的统计特性。

1 模型和数据分析

1.1 正态分布模型

依据概率论中的中心极限定理，正态分布是我们日常生活中最常遇到的，用途最广的最重要的分布。如果随机变量X的概率密度函数为：

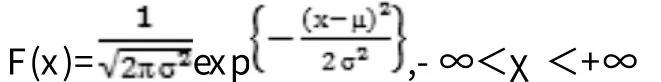
其中参数μ为任意实数，参数σ＞0，则称X为参数（μ,σ2）的正态随机变量，称X的分布为服从参数为μ,σ2的正态分布。

对于分布为N（μ,σ2）的随机变量X，我们还有：

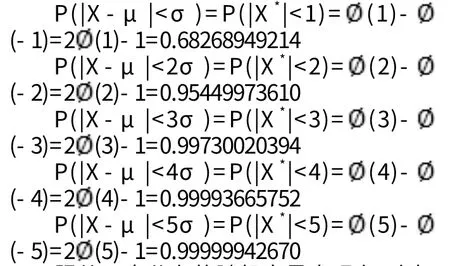
服从正态分布的随机变量出现在1个标准差之外的概率约是31.73%，出现在两个标准差之外的概率约是4.5%，出现在3个标准差之外的概率是0.27%，而出现在4个标准差之外的概率则是0.006335%，出现在5个标准差外的概率为0.000057%。也就是说，出现大于三个标准差的收益率数据的概率约是千分之二点七，出现大于4个标准差的收益率数据的概率约是十万分之六，而出现大于5个标准差的收益率数据的概率约是百万分之零点六。以股票交易为例，一年的有效交易日约为250个交易日，以日收益率计算，理论上大约一年半时间出现一次收益率超过三个标准差的交易日，66年左右出现一次收益率超过4个标准差的交易日，6700年才能出现一次收益率超过5个标准差的交易日。

在金融学中，人们通常假设股票价格遵循随机游走性质，即遵循马尔科夫过性质。马尔科夫性质隐含了在将来任一特定的时刻的股票价格的概率分布仅仅取决于股票当前的价格。股价的马尔科夫性质与强式有效市场相一致，也就是说，一种股票的当前价格已经包含了到目前为止的所有已知信息，当然包括了所有过去的价格信息。股价行为模型可以用维纳过程来刻画，维纳过程是马尔科夫过程的一种特殊形式。

设变量z遵循维纳过程。考虑在小的时间间隔上变量z值的变化。设一个小的时间间隔长度为△t，定义△z为在△t时间内Z的变化。要使z遵循维纳过程，△z必须满足两个性质：

性质1：△z与△t的关系满足

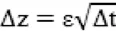
其中ε为服从标准正态分布的随机值。

性质2：对于任意两个不同时间的间隔，△t，△z的值相互独立。

从性质1，可知△z具有正态分布

E(△z)=0

Var(△z)=△t

性质2隐含z遵循马尔科夫过程。在具有任意长度为T的时间间隔内，设

其中εi（i=1,2,…..,N）是独立同分布标准正态分布的抽样值。

因此，

E[z(T)-z(0)]=0

Var[z(T)-z(0)]=N△t=T

对于一般性的维纳过程x，若其漂移率（即单位时间平均漂移）的期望值为a，方差率（即单位时间的方差）的期望值为b2，Ito过程的数学表达式为

dx=a(x,t)dt+b(x,t)dz

用S表示股票价格，根据Ito定理，股票价格遵循维纳过程

dS=μSdt+μSdz

其中为μ股票价格的预期收益率，σ为股票价格波动率。

那么，股票价格服从对数正态分布

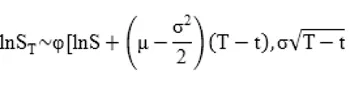
将t与T之间股票连续复利收益率定义为，

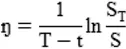
可以推出

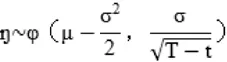
因此，如果股票价格服从对数正态分布，则有股票连续复利的收益率 服从均值为，标准差为的正态分布。

1.2 数据采集

本文采集了上证指数1990年自2012年的数据。收益率计算公式采用对数收益率：

偏度系数（skewness）计算公式：

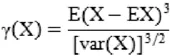
γ(X)不依赖度量单位的量，反映了随机变量X的分布关于其均值不对称的程度。

峰度系数计算公式：

对于正态随机变量X，γ(X)=0，κ(X)=0。偏度系数和峰度系数可以度量一个随机变量与正态分布的差异程度。一般将峰度系数大于0的分布称为厚尾分布。

图1是1990年～2012年上证指数日收益率，从图1可以看到，总体上上证指数日收益率波动率较大。特别是在发展初期，市场的收益率的波动剧烈，随着时间的推移，收益率的波动总体上降低。在上海股市成立之初的前四年，上证指数的最大日涨幅为72%，发生在1992年5月21日，上证指数最大日跌幅为-17.91%，发生在1995年5月23日。在2007～2008期间上证指数大幅上涨后又迅速下跌，日收益率的波动增加。

由于上证指数在1990～1992期间波动过于剧烈，且市场初创，数据可能不足以说明问题，故为了比较，采集了两组数据（1990.12.19～2012.11.8和1993.1.1～2011.11.8），一组含全部交易时间，另一组不含1990～1992的交易数据。为比较不同时间段的数据，分时数据也采集了两个时间段（2011.12.15～2012.1.9和2012.9.10～2012.9.28）的数据。在时间周期上，选择了年度、季度、月度、周、日、小时、半小时、15分钟、5分钟等9个时间周期。 样本数如下：1990.12.19～2012.11.8期间，年度收益率数据23个，季度收益率数据85个，月度收益率数据253个，周收益率数据1063个，日收益率数据5140个。1993.1.1～2012.11.8期间，年度收益率数据21个，季度收益率数据80个，月度收益率数据239个，周收益率数据998个，日收益率数据4830个。2011.12.15～2012.1.9期间分时数据：60分钟收益率63个，30分钟收益率127个，15分钟收益率255个，5分钟收益率767个。2012.9.10～2012.9.28期间分时数据：60分钟收益率59个，30分钟收益率119个，15分钟收益率239个，5分钟收益率719个。

1.3 统计分析

本文使用SPSS16.0计算。描述性统计数据见表1、表2、表3。从直方图绘出正态分布曲线直观看出，所有数据组偏离正态分布。年收益率数据由于样本数较少，两组数据不符合正态分布且差异不大。季度收益率数据两组差异较大，且第二组数据与正态分布的拟合较好。月度收益率数据尖峰明显，两组离群值都有。周收益率数据尖峰明显，两组均有离群值。日收益率数据同样尖峰明显，且两组也都有离群值。分时收益率数据正态分布曲线拟合稍好，离群值也比较少。

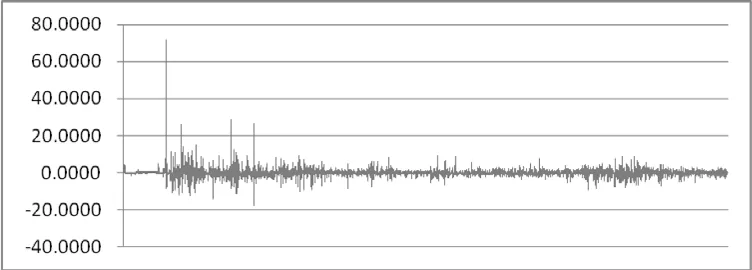
图1 1990年～2012年上证指数日收益率

表1

表2

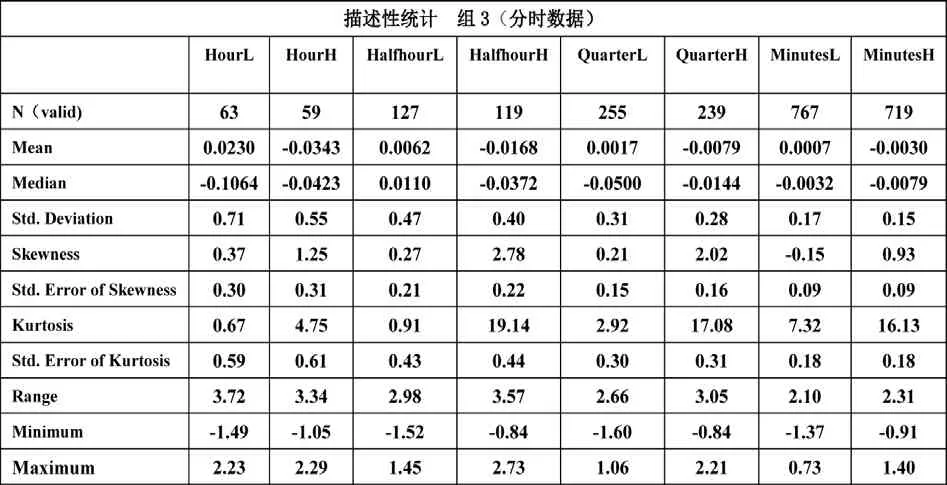
表3

表4

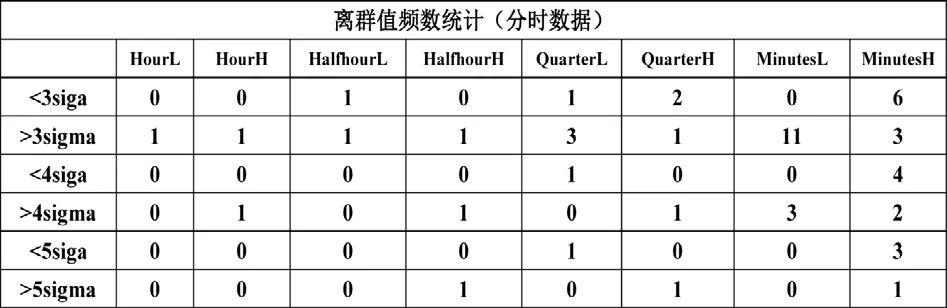
表5

使用描述性统计量进一步分析可以有更多的认识。在组1、组3中，除了年收益率数据和5分钟收益率数据偏度小于0，其它时间周期的收益率数据偏度均大于0 。所有时间周期的收益率数据的峰度均大于0 。除了年、小时、半小时的数据外，其它周期的数据峰度显著大于0 。在组2中，除了年收益率数据偏度小于0，其它时间周期的收益率数据偏度均大于0 。所有时间周期的收益率数据的峰度均大于0 。不过，与组1相比，本组由于剔除了1990～1992的数据，峰度均大幅度变小。季度收益率数据的峰度已接近0，与正态分布曲线拟合较好。

关于均值和方差的稳定性问题在描述性统计中也可以探讨。从表2 中可以看到，在1993～2012期间的年、季度、月、周、日收益率数据的均值基本稳定，然而方差不稳定。从表3中看到，2011年冬季的分时数据收益率与2012年秋季相比，均值和方差都是极端不稳定。这可能由于数据时间段较短，市场所处的涨跌周期不同所致，当然更可能是金融时间序列的异方差导致。

另一个不可忽视的现象是离群值问题，也就是收益率数据的极端值大于理论概率分布的问题。从表4、表5中可以看到，在相同的时间段，随着时间周期的变化和样本数量的增加，离群值的数量也在不断增加。前文计算表明，以股票交易为例，一年的有效交易日约为250个交易日，以日收益率计算，理论上大约一年半时间出现一次收益率超过三个标准差的交易日，66年左右出现一次收益率超过4个标准差的交易日，6700年才能出现一次收益率超过5个标准差的交易日。在周数据和日数据中，不仅有相当多的样本值大于3个标准差，大于5个标准差也不少。在日收益率数据4830各样本值中，超过3个标准差的有82个，超过4 个标准差的有36个，超过5个标准差的有19个。在分时数据各个时间周期收益率数据中，同样出现相当多的极端值。极端值的频繁出现从另一个侧面反映出市场的非理性。

2 分析与讨论

由上述统计分析可以得出结论，绝大多数情况下，各种时间周期的收益率分布数据并不能与正态分布拟合较好。以正态分布作为各种金融模型的统计分布基础，会给模型计算带来较大误差，时间跨度越大，离群值的影响越大。收益率数据中大于3个至5个标准差的离群值远远多于理论估计，造成这种现象的原因有多种。在很大程度上，金融市场属于正反馈混沌动力系统，市场的非理性广泛存在，难以用完全理性的模型来近似市场，强式有效市场并不存在。长期资本公司的失败在很大程度上也是由于以经典理论为基础构建的金融模型崩溃所致。

金融市场是全世界参与主体数量最多、资金流动最大的市场，其复杂性到目前还没有现成的模型可以完全刻画。为了在实践中克服金融时间序列数据的非正态、均值不稳定以及异方差等问题，一方面需要发展更好的计量金融模型，另一方面也需要采用借鉴行为金融学的理论，以技术分析弥补经典统计模型的不足。

[1]龚光鲁.概率论与数理统计[M]. 北京：清华大学出版社，2006

[2]John C. Hull. 期权、期货和其它衍生品[M].北京：华夏出版社，2000

[3]约翰·Y.坎贝尔，安德鲁·W.罗，艾·克雷格·麦金雷.金融市场计量经济[M].上海：上海财经大学出版社，2003

[4]劳兰珺，邵玉敏.行业股票价格指数波动特征的实证研究[J].南开管理评论，2005，(5)：4-8

[5]余为丽.基于极值理论的VaR及其在中国股票市场风险管理中的应用[D].武汉,华中科技大学，2006

[6]朱宏泉.中国股票市场收益率与风险的实证分析[D].北京，中科院数学与系统科学研究院，2000