基于DEA方法的科研项目验收绩效评估系统研究

张继将

上海数据分析与处理技术研究所，上海 201112

引言

科研项目验收绩效评估是科研管理的重要工作，也是典型的绩效评估问题。目前验收科研项目，大多采用线性权重法，追求产出最大化，而对绩效考虑偏少。在不断加大科研投入的同时，必须努力使有限的投入发挥较大的效益。因此，严把验收关，对科研项目的验收进行绩效评估作用尤为重要。

目前，常见的绩效评价方法种类很多，例如层次分析法，模糊综合评价法，人工神经网络分析法，灰色评价方法，数据包络分析法等[1]。

层次分析法是一种多准则决策方法。它把一个复杂问题表示为有序的递减层次结构，通过人的判断对决策方案优劣进行排序。这种方法能够统一处理决策中的定性与定量因素，具有实用性、系统性、简洁性等优点。它依靠主观评价做出优劣排序，所需数据量很小，决策花费的时间短。但是当遇到因素多、规模较大的问题时，层次分析法德在主观上不好把握。

模糊综合评价是应用模糊关系合成原理，从多个因素对评判事物隶属等级状况进行综合性评判的一种方法。不仅可以对评价对象按综合值的大小进行评价和排序，而且还可根据模糊评价集上的值，按最大隶属度原则去评定对象所属的等级。结果包含的信息量比较丰富。模糊综合评价方法的不足之处是，它不能解决评价指标间相关造成的评价信息重复问题，隶属函数的确定没有系统方法，而且合成的算法也有待进一步探讨。

人工神经网能够络评价法是一种交互式的评价方法，它可以根据用户期望的输出不断修改指标的权值，直到符合实际为止。该方法对于弱化权重的人为因素是有益的，而且具有学习机制，尽可能消除以往权重设置中的人为因素影响，保障权值的有效性和实用性。缺点是，没有显性含义的共识，变量间权重的含义难以解释，而且需要大量的样本数据来训练模型，计算复杂，只能借助于计算机来完成。

灰色评价方法是利用灰色关联确定各评价指标与理想指标的关联程度，进而根据关联值确定各评价方案的优劣次序。灰色评价法是一种定性分析和定量分析相结合的综合评价方法，可以较好的解决评价指标难以准确量化和统计的问题，排除了人为因素的影响。评价结果较为客观准确，计算量小，过程简单，无需大的样本，可靠性强。该方法是一种相对比较，不反应绝对指标。

1978年由著名的运筹学家A.Charnes， W.W.Cooper和 E.Rhodes首先提出了一个被称为数据包络分析（Data Envelopment Analysis，简称DEA）的方法[2]，评价部门间的相对有效性（因此被称为DEA有效）。魏权龄教授于1988年出版了国内第一本DEA研究专著[3]，严格、系统地论述了DEA方法与模型，给出了DEA的理论框架。DEA方法一出现就以其独有的特点和优势受到了人们的关注，不论在理论研究还是在实际应用方面都得到了迅速的发展[4][5]，并取得了多方面的成果，现已成为管理科学、系统工程和决策分析、评价技术等领域中一种常用而且重要的分析工具和研究手段。DEA方法是评价多输入、多输出同类部门（或单位）间相对有效性的一种重要方法。

1 绩效评估指标体系构建

本文设计的评估指标体系从项目的投入和产出两部分分析。我们结合科研项目实际情况和评估模型对评估指标的要求，依据指标细化原则，将投入和产出指标细化得出表1所示的指标体系。

由于评价过程中，各项指标的地位和作用是不同的，根据层次分析法（AHP），对表1中的指标进行专家调查和分析，得到各项指标权重表如表2所示。注意到这里的权重是归一化二级指标项，使得各二级指标都归一化到[0-1]范围，因此二级指标中各项的权重和为1。

对于预研性的项目，产出的评价主要看成果的专利、高水平论文以及是否解决国家和重要部门中急需解决的关键问题，直接经济效益不是主要的。设置各项指标的权重后，将其带入DEA方法构建的模型中计算。

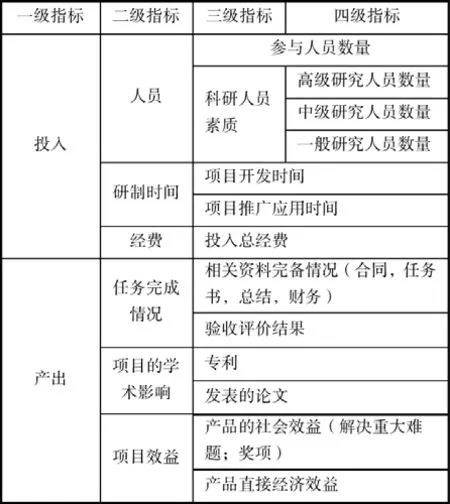
表1 项目评估的指标

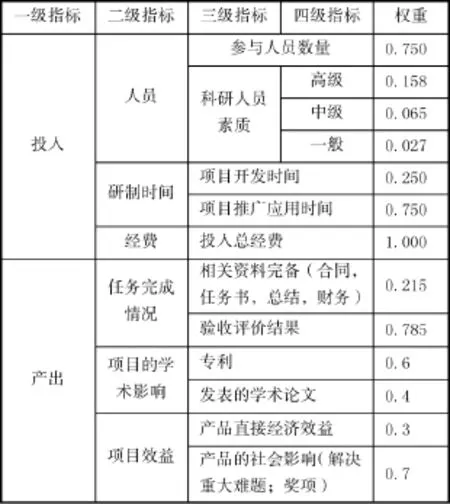
表2 指标体系权重表

2 基于DEA方法的绩效评估建模

使用DEA方法进行绩效评价时，我们可以按照图1所示的流程进行[6]。

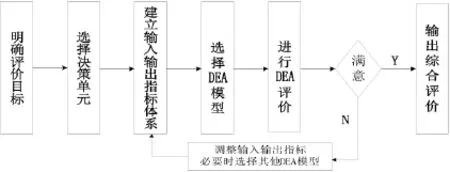
图1 DEA方法绩效评估流程图

即首先明确评价目标，对决策单元进行分析，带入DEA模型计算并得出评价结果。

科研项目的绩效评估属于典型的多输入多输出问题，这里我们采用CCR模型进行计算，将每一个待评估项目看做一个决策单元（DMU）。设有n个DMUj (1≤j≤n) ，这n个决策单元都具有可比性。每个决策单元都有m种输入和s种输出，输入输出见图2。

图2 多决策单元输入输出数据

其中，xij=D M Uj对第i 种输入的投入量，xij>0，记Xj=(x1j,x2j,...xmj)T，j=1,...n。

yrj=D M Uj对 第r 种 输 出 的 产 出量，yrj>0，记为Yj=(y1j,y2j,...ysj)T，j=1,...n。

对 输 入 变 量 的 权 重 记 为v=(v1,v2,...vm)T；输出变量的权重记为 u=(u1,u2,...us)T。

CCR模型可以表示为：

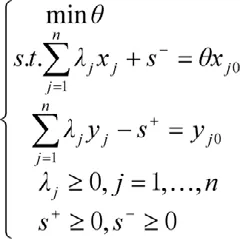
（1）当上式的最优值等于1，则决策单元j0为弱DEA有效。反之亦然。

在使用CCR模型对决策单元的有效性进行评估的过程中，会出现多个决策单元同时有效的情况，这些有效的决策单元之间无法用CCR模型进一步进行有效程度的评估比较。这时引入超效率DEA模型，对有效决策单元之间的效率进行比较。

超效率DEA模型的基本思路是：在评估某个决策单元的时候，将该决策单元排除在决策单元的集合之外，通过将该决策单元的投入和产出被其他所有其他决策单元的投入和产出的线性组合代替的方法，使得有效决策单元之间也能比较效率的高低。从而实现所有决策单元的充分排序。

通过CCR模型与超效率模型相结合的方法，我们可以得出科研项目之间的效率排名以及各决策单元调整投入的幅度，扩大产出的可能方向和程度。

3 科研项目验收绩效评估案例分析

根据2012年7月xx市验收的6个科研项目，我们采用数据采集，调查问卷，查询记录等方式，对其进行了一定了解。采用本文提出的DEA方法，对6个科研项目验收的绩效进行评估。发现问题，给出结论和改进方向并解决问题。

我们评价六个科研项目，分别把这六个项目作为决策单元（DMU）。为了简化计算，我们将三、四级指标与权重计算后转化为二级指标带入CCR模型进行计算，通过对项目的投入和产出数据的采集，我们得到的数据表3。

其中投入I1表示人员，单位为人；I2表示研制时间，单位为天；I3为研制经费，单位为万元。产出以百分制打分（专家打分），包括产出O1为任务完成情况；O2为项目的学术影响；O3为项目效益。将数据代入CCR模型中进行计算，获得计算结果如表4所示。

由计算结果显示DMUj (j=1，5)为DEA有效，不存在投入和产出冗余，投入冗余和产出冗余都为零。无效的（低效）决策单元为DMUj（j=2，3，4，6），即存在投入或者产出冗余。计算所得为6个科研项目的相对效率值。表4中所示产出投入冗余均为相对值，而非绝对值。其中，投入冗余表示该在相应项目上的投入存在过投入的情况；输出冗余则表示该单位在此项目上存在输出不足的情况。通过表4的结果，我们可以得出如下结论，低效单元普遍存在经费投入过量的问题，其中DMU2和DMU4存在人员投入过量，DMU4和DMU6存在研究时间过长的问题。

对于DMU1和DMU5，仅仅通过CCR模型无法比较出两者的优劣，此时我们利用超效率DEA模型对其进一步计算。如表5所示。

通过对DMU1和DMU5进行超效率DEA模型分析，发现DMU1>DMU5，DMU6的研究时间应进一步缩短，项目效益应提高。即6个科研单位的绩效排序为DMU1>DMU5>DMU6>DMU2>DMU3 >DMU4 。

对于产生的冗余，我们可以用如下方法进行修正。设某DMU的效率为θ，投入冗余为S，输出冗余为O。我们可以得到其优化的投入和产出值，改进的公式如下：

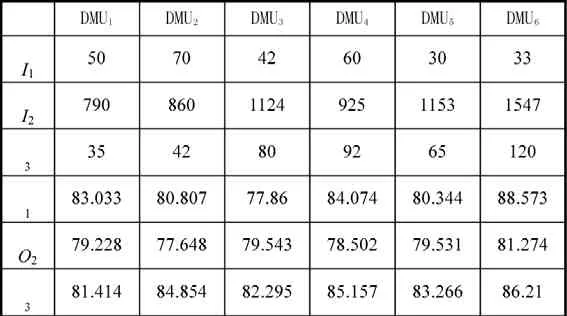
表3 决策单元数据表

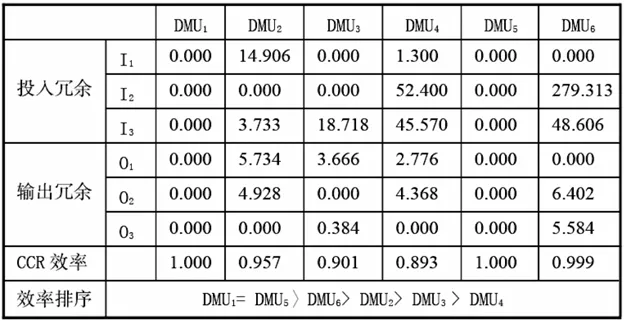
表4 CCR模型计算结果表

表5 超效率DEA模型计算结果表

其中S,O为当前投入产出值，S',O'为当前投入产出值为优化后的投入产出值，通过优化值与当前值作对比，即可量化投入产出的改进程度，为科研单位提供了参考方案，有助于单位改进方法，提高效率。

4 结语

本文提供了一种通过建立指标体系，用DEA的多种模型分析计算的方法，对科研项目验收过程中的指标绩效进行了评估，对决策单元的相对效率进行了排序，并提供了改进公式。通过一个案例验证该方法的有效性，为相关部门对科研院所所承担的项目验收绩效排序提供了一种可操作的思路。DEA方法有一套复杂的模型体系，衍生的模型也有许多。研究人员可以进一步探索DEA方法在项目评价中的应用，得出更科学的评价结果。

[1]谭跃进，陈英武，易进先.系统工程原理.[M].长沙:国防科学技术大学出版社，2008

[2]Charnes A，Cooper W. W，Rhodes E. Measuring the efficiency of decision making units. European Journal of Operational Research，1978，2：429-444

[3]魏权龄.数据包络分析.北京：科学出版社，2004

[4]马占新.数据包络分析模型与方法.北京：科学出版社．[M]，2010，1-10

[5]盛昭瀚，朱乔，吴广谋. DEA理论、方法与应用，1996

[6]Andersen P Petersen N C.A Procedure for Ranking Efficient Units in Data Envelopment Analysis[J].Management Science，1993