相继两个正整数平方和中的素数方幂

管训贵

(泰州师范高等专科学校数理信息学院，江苏泰州 225300)

1 引言及主要结论

设N*，P分别表示全体正整数和素数的集合.1967年，E.L.Cohen［1］借助于计算机证明了方程:

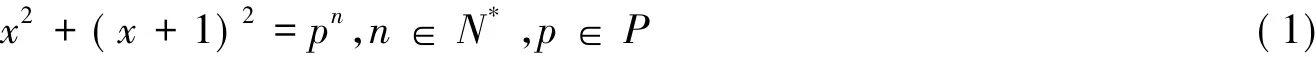
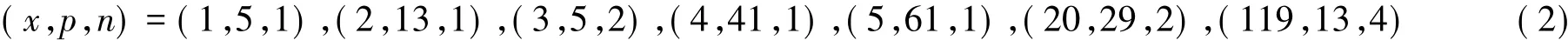
适合p≤109的解仅有:由于该问题是经典的多项式表素数问题的推广，并且与阶为素数方幂的有限单群的存在性问题有着直接的联系［2］.因此，研究方程(1)的解具有一定的理论价值.

2000年，李中［3］证明了方程(1)适合 p＞109 的正整数解(x，p，n)都满足 n≤2.由此及式(2)可知，除了(x，p，n)=(119，13，4)这一情况外，当方程(1)成立时，则必有 n=1 或2.

本文找到了方程(1)在p＜6×106时的全部正整数解，即以下结果.

定理1 若素数p＜6×106，则当n=1时，方程(1)共有365组正整数解(x，p)，其解数分布如表1所示.

表1 解数分布表Tab.1 Distribution of the number of solution

定理2若素数p＜1×1016，则当n=2时，方程(1)仅有6组正整数解:

2 关键性引理

引理1若n=1，则方程(1)中x必满足x=1或x≢1，3，6，8(mod 10).

证明若n=1，则方程(1)成为:当x=1时，p=5是素数，结论成立.

当 x≠1 且 x≡1(mod 10)时，p≡5(mod 10);同样当 x≡3，6，8(mod 10)时，也有 p≡5(mod 10).此时，5∣p，与p为素数矛盾.引理1得证.

引理2方程x2+(x+1)2=z2的全部正整数解由递推式:

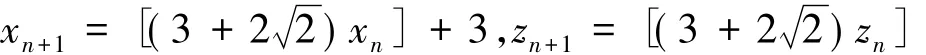
及x1=3，z1=5，n∈N*，给出，其中［α］表示实数α的整数部分.

证明参见文献［4－5］.

3 定理的证明

先证定理1.

考虑到n=1，p＜6×106时，1≤x≤1731，结合引理1并利用计算机可算出方程(1)满足p＜6×106的全部正整数解为:

再证定理2.

由引理2 知，z1=5，z2=29，z3=169=132，z4=985=5×197，z5=5741，z6=33461，z7=195025=52×29×269，z8=1136689=137×8297，z9=6625109=37×179057，z10=38613965=5×132×45697，z11=225058681=229×982789，z12=1311738121=29×1549×29201，z13=7645370045=5×53×197×146449，z14=44560482149，z15=259717522849=61×1301×3272609，z16=1513744654945=5×5741×52734529，z17=8822750406821=132×29×1800193921，z18=51422757785981=593×78737×1101341，z19=299713796309065=5×389×33461×4605197，z20=1746860020068409，z21＞1×1016.

因为 z3，z4，z7，z8，z9，z10，z11，z12，z13，z15，z16，z17，z18，z19均为合数，所以当 n=2 时，方程(1)满足 p＜1×1016的正整数解仅有6组，即式(3).定理2得证.

综上，若素数 p＜6×106，则方程(1)共有 370 组正整数解(x，p，n)，推广了文献［1］中的结论.

［1］Cohen E L.On the sum of the squares of two consecutive integers［J］.Math Comp，1967，21:460－465.

［2］陈重穆.关于有限单群的阶［J］.数学学报，1987，30(5):605－613.

［3］李中.两个连续正整数平方和中的素数方幂［J］.吉首大学学报:自然科学版，2000，21(1):30－31.

［4］管训贵.关于丢番图方程 x2+(x+p)2=z2［J］.湛江师范学院学报，2009，30(6):46－49.

［5］管训贵.关于丢番图方程x(x+1)(x+2)=2pyn［J］.湖北民族学院学报:自然科学版，2012，31(4):404－408.