等距特征映射的支持向量机模型在上市公司信用风险评估中的应用

李菲雅，邓 翔

（1．四川大学 经济学院，四川 成都 610064；2．四川师范大学 政治教育学院，四川 成都 610068）

一、引 言

信用风险是银行贷款或投资债券时发生的一种风险，即借款者违约风险。以企业财务数据及相关资料为基础，建立数学模型对其进行科学地分析和度量，是建立风险管理系统和管理流程的有效途径。

作为证券市场基石的上市公司是否诚信的问题，一直困扰着我国证券市场的稳定和发展。我国上市公司失信现象普遍存在，其深层原因在于内部治理结构不完善、外部监督控制机制不健全。随着2001年“银广夏事件”、2002年“蓝田事件”、2004年“德隆事件”、2005年“科龙事件”的接连发生，上市公司信用风险监控已经成为我国金融机构面临的核心问题，它不仅直接影响现代社会经济生活的各个角落，也间接影响到一个国家的宏观经济政策和经济发展。我国商业银行内部的信用评级水平比较落后，信用风险度量管理体系尚不健全，对信用风险的分析多处于传统的定性分析阶段，远不能有效满足商业银行对信用风险控制与管理的要求［1］。因此，建立完善的金融风险预警、计量和控制体系对我国经济的稳定发展具有重要的现实意义。

二、文献综述

近年来，随着金融工程理论、信息技术的飞速发展，国际银行业在风险管理领域取得了突破性进展，在实践中创立了许多识别和量化风险的技术，并相继出现了一些对银行风险从识别、衡量、评价到控制管理的信用风险度量模型。传统的风险度量模型主要有判别分析（Altman，1968）、Logistic 回 归 （Brumbaugh，1989）、聚 类 分 析（Robert，1992）等多种方法，其中著名的包括 Al tman的Z－score及在此基础上改进的ZETA模型（Altman，1997），以及数学规划，贝叶斯决策模型等方法。综合来看，这些方法综合分析能力总体较差，且缺乏整体概括，定量评价结果精度都不高［2－3］。

鉴于传统分析法的不足，现代信用风险度量与管理模型以经济金融理论的创新性发展（如信息经济学、期权定价理论、套利定价理论、资本资产定价理论等）为基础，依靠大量数学工具、计算机技术，建立高维的风险模型。这些模型协助银行家进行贷款决策、开发市场、信用评估等，大大提高了各银行的风险管理效率。目前国际上运用较多的现代信用风险度量模型主要有以下几种［4－8］。

KMV公司的KMV模型。1993年，世界著名的信用风险咨询管理公司KMV利用布莱克－斯科尔斯－莫顿模型提出了信用监测模型（Credit Monitor Model）。该模型将银行的贷款问题倒转一个角度，从借款企业所有者的角度考虑贷款归还问题。基本原理是企业所有者相当于持有违约或不违约的选择权，债务到期时，若企业资产的市场价值超出其负债价值，企业愿意还债，将剩余部分留作利润；如果企业资产价值小于负债水平，全部资产也不能完全偿债，企业会选择违约，将公司资产转交给债权人。此后，Longstaff和Schwarz（1995）、Zhou（1997）对此作了进一步的研究。

JP摩根的信用度量术模型（Creditmetrics Mode1）。1994年J．P．Morgan在其1987年信用转换矩阵的基础上，提出了基于受险价值（Valueat Risk，VaR）的市场风险度量模型，即Risk Metrics。该模型的核心思想是组合价值的变化不仅受到债务人违约的影响，而且还会受到债务人信用等级转移的影响。该模型通过求解信贷资产在信用品质变迁影响下的价值分布，计算信用风险的VaR值（即在给定的置信区间上、给定的时段内，信贷资产可能发生的最大价值损失），通过预测借款人信用等级的变动，得出信用等级转移概率矩阵。此后，Jonesand Mingo（1999），Nyfeler（2000），Forestand Kpmecpeat（2000），对此作了进一步的解释和拓展。

瑞士信贷银行的信用风险附加法模型（Crid etrisk＋）。瑞士波士顿第一银行产品部在1997年开发了源于保险精算学思想的信用风险附加法模型（Credit Risk＋ Model）。该模型运用保险经济学中的保险精算方法，基本思路是违约率的不确定性和违约损失的不确定性都很显著，应按风险暴露大小将贷款组合划分成若干频段，以降低不精确的程度。

神经网络模型（Neural Networks）。传统的统计方法对输入变量有一些限制性假设，如线性、正态分布、相互独立等，但实际的变量常违反这些假设。神经网络模型并不需要这些假设，Coats和F ant（1993）与Tam和 Kiang（1992）采用了神经网络分析法分别对美国公司和银行财务危机进行了预测，P iramuthu等（1999）研究比利时企业信用，在神经网络中使用了特征提取技术，Martinelli（2006）对决策树和神经网络模型进行了对比研究，Chen（2007）则提出了具有概率特性的神经网络模型。这些模型在一些国家的实证研究取得较好的效果。

从国内已有成果看，我国也有不少学者对信用风险评估问题进行了深入的探索和研究。例如，韩东平等（2006）以2003－2006年ST（“特别处理”）上市公司为研究对象，选取14个现金流指标建立了一个多元判别财务预警模型，该模型在财务危机发生前一年和前两年判别精度分别为93．3%和83．7%［9］。姜秀华、孙铮（2001）以2000年11月20日为基准点，选取了沪、深证券交易所的84家上市公司（ST和非ST公司各占一半），筛选出4个财务指标建立了Logistic判别模型，财务危机发生前一年对ST（“特别处理”）公司与非ST（“特别处理”）公司判定准确率分别为88．10%和80．95%［10］。上述多元判别分析、Logistic回归等传统评估方法局限于在假设条件下，用线性决策函数来描述信用风险与财务数据之间的非线性映射关系，存在明显缺陷。

神经网络能较好拟合二者之间的非线性关系，且无严格的假设限制，已成为信用风险评估的重要方法。杨淑娥、黄礼（2005）采用BP人工神经网络（BPNN）工具，以120家上市公司的截面财务指标作为训练集，并使用同期的60家公司作为测试集，建立了财务危机预警模型，取得了训练样本90．8%和测试样本90%的判正率［11］。但神经网络也存在收敛速度慢，易陷入局部极小等缺点，加之该方法没有统计理论基础，解释性不强，应用受到很大限制。

另外，财务数据特征提取是信用风险评估的重要前提，财务指标种类繁多、差异迥然，包含了盈利能力、偿债能力、成长性、结构性等若干大类，简单地将所有指标简化或合并，会造成大量有用信息的丢失或重叠，从而影响评估精度。李杏（2009）用逐步判别法［12］、刘淑莲等（2008）用因子分析和聚类分析法［13］、刘彦文等（2007）用粗糙集理论［14］等方法对上市公司的财务指标进行了属性约简。上述方法是线性提取，操作简单且易于实现，然而财务数据存在非线性结构，应用这些方法往往不能取得满意结果。

针对上述现状，本文采用Isomap和S VM相结合的思路建立数学模型。拟利用支持向量机（S VM）遵循结构风险最小化原则，能够解决小样本、非线性和高维的信用风险问题的优势；等距特征映射（Isomap）算法同时具有线性降维、可有效降低信用风险评估模型的复杂结构且支持向量机分类识别的特点，尝试建立Isomap－S VM信用风险预警模型，并与BPNN（BP神经网络）、PCASVM（主成分－支持向量机）模型预测效果进行实证比较研究。

三、基于Isomap的S VM模型构建

（一）Isomap算法

Isomap是Tenenbaum［15］在2000年提出的一种基于距离保持的非线性特征提取方法，核心思想是保持点对之间的测地距离，算法如下：

1．构造近邻赋权图G

将X中每一个点与所有点进行比较，当满足公式（1）就认为它们是相邻的。

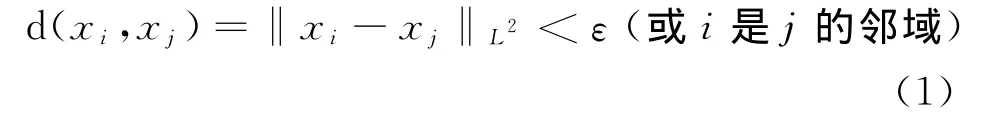
式中：d（xi，xj）为两点之间的欧氏距离；ε为固定半径。将边长为d（xi，xj）的点连接起来即得到近邻赋权图G。

2．计算测地距离矩阵DG

在近邻赋权图G上，利用Dijkstra算法［16］计算两点之间的测地距离

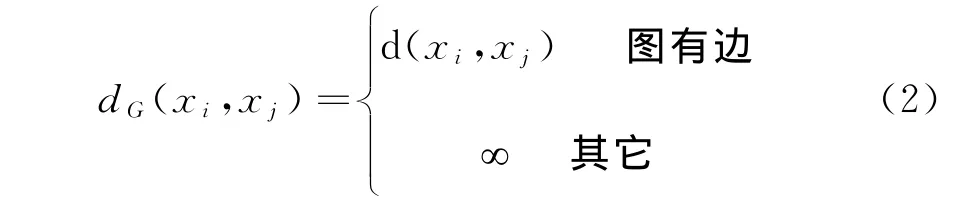
对于所有的k＝1，2，…，N ，利用下列公式最小化测地距离

由近邻赋权图中所有点对的最短路径组成距离矩阵DG＝｛dG（xi，xj）｝。

3．应用传统的MDS算法计算距离变换矩阵

式中：H 是与DG同阶的单位矩阵。

记τ（DG）的最大q个特征值λ1，λ2，…，λq所对应的特征向量为u1，u2，…，uq，所构成的矩阵为U＝［u1，u2，…，uq］，则得到q维低维嵌入数据Y 。

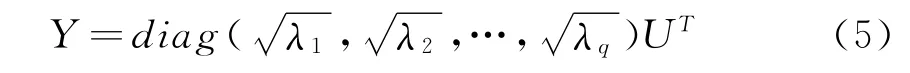
4．定义残差E来衡量降维的误差，以确定降维的维数d，定义残差如下式

式中：R2为线性相关系数；DY是d维空间中的欧式距离矩阵。

一般来说，降维的维数d越大，残差越小。确定d有2种情况，一是残差曲线出现拐点，二是残差小于一定的阈值。

（二）SVM 算法

S VM算法是由V．Vapnik等人于1 995年在统计学理论基础上提出的一种新的学习方法［17］82－108，可以有效地实现对基于小样本的高维非线性系统精确拟合，并且采用结构风险最小化原则，具有很好的泛化能力。

式中：w为权向量；b为分类阈值。

若得到上面的最优分类超平面，就可以用其来对测试集进行预测了。最优超平面可以通过解下面的二次优化问题来获得：

满足约束条件：yi（w·xi＋b）≥1

根据泛函的有关理论，只要一种核函数满足Mercer条件，它就对应某一变换空间中的内积，因此结合Lagrange方法在线性不可分的情况下，把上述二次规划问题转换为对偶问题，即

式中：C为误差惩罚系数；ai为Lagrange乘子；K （xi·xj）为核函数。

采用适当的核函数可实现某一非线性变换后的线性分类，而计算的复杂程度没有增加。S VM常用的核函数包括线性、多项式、径向基和多层感知器等，本文采用高斯核函数，描述为：

根据分类函数的正负可判断样本所属的类别，相应的分类决策函数为：

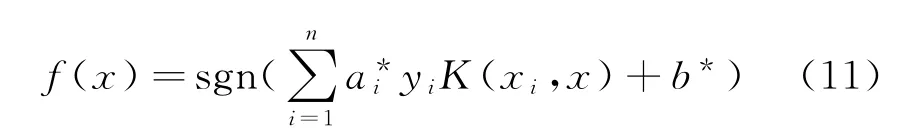
式中：sgn为符号函数；为最优Lagrange乘子；b＊为最优分类阈值。

根据以上分析，模型将通过求解一个二次规划问题得到的决策函数来对信用风险进行评估。

（三）计算步骤

传统的构建线性函数来评估信用风险，这种方法费时且不一定最优。利用Isomap－S VM算法对其进行评估是一种有效的手段，具体过程如下：步骤1：采集上市公司数据样本集，并选择财务指标；步骤2：利用Isomap算法对数据样本集进行降维，得到低维嵌入数据；步骤3：选择S VM核函数，并用遗传算法优化参数σ和C；步骤4：将低维嵌入数据中的训练样本输入S VM模型进行训练，得到支持向量；步骤5：用低维嵌入数据中的测试样本对训练后的模型进行检验、评价。

四、实证检验分析

（一）数据来源与样本选取

本文数据来源于CCER经济研究中心色诺芬数据库①CCER中国经济金融数据库系统由北京大学中国经济研究中心和北京色诺芬信息服务公司联合开发，并在国内第一家推出基于互联网的BS数据服务平台，该服务系统全面涵盖了中国资本市场、货币市场、宏观经济及行业经济的所有研究领域资料。。由于我国证券市场的退市制度不完善，退市的企业不多，所以多数研究选择因“财务状况异常”而被“特别处理（Specia lTreatment，ST）”作为企业陷入财务危机的标志。根据上市公司披露制度，上市公司在t年是否被“特别处理”是由其t－1年财务报告的公布所决定的，这两个时间几乎是同时发生，用t－1年的财务报告数据来预测上市公司t年的状态应用价值不大。另外，如果一个公司在t－1年有利润，那么该公司即使在t－2年亏损，它在t年时也不会被“特别处理”；而如果一个公司在t－1年亏损，基于这一年数据对t年“特别处理”的预测将变成简单的对t年亏损还是盈利的预测。使用“特别处理”之前第三年的数据，则不存在这些问题［18］54－55。此外，何沛俐、章早立（2002）通过利用时序样本实证研究发现，在t－4年时，财务危机企业与正常企业之间的差异是不明显的［19］23－28。

因此，本文选取上市公司被“特别处理”之前的第t－3年截面数据为样本的时间范围，非“特别处理”公司财务数据按照其所对应的年份选取。样本的数量范围，选取沪、深证券交易所2009年100家上市公司作为训练样本，2010年100家上市公司作为测试样本，样本分布如表1所示。原始财务数据略（数据来源于CCER经济研究中心色诺芬数据库）。

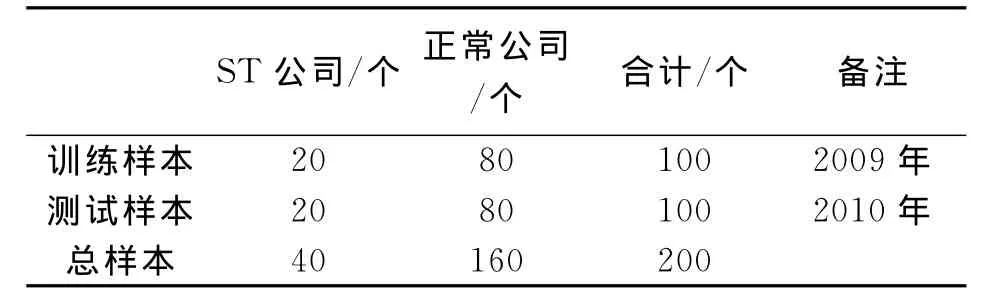
表1 样本数量分布情况

（二）指标选取

从目前来看，在上市公司信用风险评估研究中，主要以公司财务指标衡量信用风险。在借鉴穆迪、标准普尔等公司资信评级指标体系的基础上，本文从偿债能力、获利能力、营运能力等6个方面选取了20个财务指标作为研究变量，构建指标体系，如表2所示。这些指标的选取既考虑了公司的资产与负债能力，同时兼顾到公司的盈利与成长能力，能够充分体现上市公司的信用状况。

表2 模型使用的财务指标

（三）数据降维

Isomap算法中邻域个数k要求大于流形的维数以提高算法的稳健性。过大会导致在高度扭曲或折叠的流形上产生短路现象，过小会导致嵌入结果的偏差过大甚至近邻赋权图不连通。本文选用“留一法”的交叉验证方式［20］确定，以评估诊断器对校验采样的误判个数Ne最低优选参数k的取值。图1为k与Ne的关系趋势曲线（d＝5），随着k的增多，误判个数先减少后增多，结合算法的稳健性最后选定k＝7。图2是邻域k＝7的情况下构造近邻图后获得的残差曲线，可见在维数是4时有拐点出现，并且残差的绝对值小于0．05。

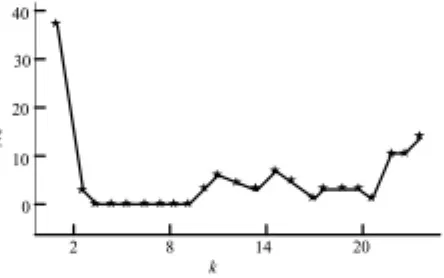
图1 不同近邻个数下的误判个数

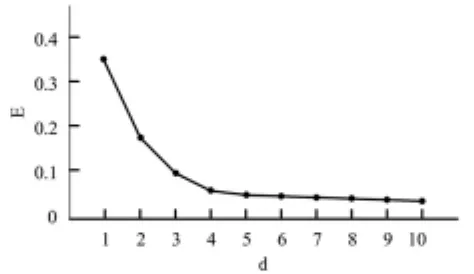
图2 残差曲线图

同时，将样本数据归一化后输入SPSS软件，进行PCA降维，当主成分提取到第5个时，它们对信息累积贡献率达到87．428%，涵盖了原始指标变量85%以上的信息（为方便比较，选择与Isomap相同的降维维数）

（四）实验结果

使 用 Matlab7 工 具 箱 函 数［21］227－265，建 立BPNN、PCA－S VM、Isomap－S VM 3种信用风险评估模型。模型参数设置如下：对于BPNN，输入输出节点数分别为20和1，输出层采用purelin函数，隐含层节点数为10，激活函数用tansig函数。S VM参数σ和C采用遗传算法优化，实数编码，最大进化代数取100，种群最大数量为20，交叉概率0．8，变异概率0．4，变化范围0．1～100，3倍交叉验证。

模型的性能通过3个指标来衡量。准确率，即评估正确的公司占总样本比例；ST误判率，即“特别处理”公司误判为正常公司的概率；非ST误判率，即正常公司误判为“特别处理”公司的概率。实验结果如表3所示。

表3 三种评估模型对比结果 单位：%

对比实验表明，S VM对训练集进行回测评估，准确率达到100%。BPNN对测试样本的评估精度较差，准确率仅为74%，平均误判率达到25%，S VM对测试样本进行评估，准确率均能达到85%以上，这表明S VM比BP NN评估识别精度高，小样本泛化推广能力强。引入非线性Isomap降维与线性PCA降维比较，S VM的评估准确率提高了5%，说明上市公司财务数据中存在非线性结构。

五、结 论

本文提出的新型上市公司信用风险评估模型将Isomap理论和S VM技术有机结合起来，既精简了模型输入维数，降低样本间的干扰，又解决了小样本下神经网络识别精度低的问题。根据研究，得出以下结论：（1）对于存在非线性结构的财务数据，传统的全局线性降维方法不能发现其低维结构。引入非线性降维算法Isomap对财务指标进行属性约简，有效降低了信用风险评估模型的复杂结构，提高了模型的评估精度。（2）神经网络是研究样本无穷大时的渐进理论，基于经验风险最小化原则，而上市公司的财务数据是有限的，这就不能保证网络的泛化能力。S VM有严格的理论和数学基础，基于结构风险最小化原则，可以有效地解决上市公司有限样本条件下的高维数据模型构建问题。经对比实验表明，S VM的评估精度明显优于BPNN。（3）S VM核函数σ和误差惩罚参数C共同影响着测试样本的分类效果和推广能力，针对目前人为选择参数的盲目性，利用遗传算法对其进行优化，达到了较好的评估效果。

［1］胡胜，朱新蓉．我国上市公司信用风险评估研究——基于Logit模型的分析［J］．中南财经政法大学学报，2011（3）：38．

［2］ALTMAN．Financial Ratio，Discriminant Analysis and the Prediction of Corporate Bankruptcy［J］．Journal of Finance，1968（12）：589－609．

［3］AIRMANR，HALDEMAN ，P NARAYANAN．Zeta Analysis：a New Model to Identify Bankruptcy Risk of Corporations，Journal of Banking and Finance，1977（4）：29－54．

［4］鲁炜，赵恒珩，刘冀云．KMV模型关系函数推测及其在中国股市的验证［J］．运筹与管理，2003（3）：43－48．

［5］COATSP，FANTL．Recognizing Financial Distress Patterns Using a Neural Network Tool［J］．Financial Management，1993（3）：142－155．

［6］PIRAMUTHUS．Financial，Credit－risk Evaluation with Neural and Neurofuzzy Systems［J］．European Journal of Operational Research，1999，112（2）：310－321．

［7］王春峰，万海晖．商业银行信用风险评估及其实证研究［J］．管理科学学报，1998（1）：68－72．

［8］章忠志，符林，唐焕文．基于人工神经网络的商业银行信用风险模型［J］．经济数学，2003（3）：42－47．

［9］韩东平，田艳丽，王悦鑫．基于现金流测量标准的财务预警实证研究［J］．财会通讯，2006（12）：48－50．

［10］姜秀华，孙铮．治理弱化与财务危机：一个预警模型［J］．南开管理评论，2001（5）：19－25．

［11］杨淑娥，黄礼．基于神经网络的上市公司财务预警模型［J］．系统工程理论与实践，2005（1）：12－18．

［12］李杏，基于基本面的上市公司投资风险——判别分析评价［J］．企业技术开发（下半月），2009（5）：36－37．

［13］刘淑莲，王真，赵建卫．基于因子分析的上市公司信用评级应用研究［J］．财经问题研究，2008（7）：53－60．

［14］刘彦文，戴红军．基于粗糙集－神经网络的财务危机预警模型实证研究［J］．科研管理，2007（11）：138－142．

［15］TENENBAUMJB，SILVAVD，LANGFORDJC．A Global Geometric Framework for Nonlinear Dimensionality Reduction［J］．Science，2000，290（5500）：2319－2323．

［16］DIJKSTRAEW．A Note on two Problems in Connexion with Graphs［J］．Numerische Mathematik，1959（1）：269－271．

［17］CRISTIANININ．支持向量机导论［M］．李国正，译．北京：电子工业出版社，2004．

［18］刘彦文．上市公司财务危机预警模型研究［D］．大连：大连理工大学，2008．

［19］何沛俐，章早立．立体空间下的全新财务危机远期预警模型［C］．深圳证券交易所第五界会员单位管理公司研究成果，2002．

［20］MARTENSHA，DARDENNEP．Validation and Verification of Regression in Small Data Sets［J］．Chemometrics and Intelligent Laboratory Systems，1998（44）：99－121．

［21］朱仁峰．精通 Matlab 7［M］．北京：清华大学出版社，2006．