一种增量式多目标优化的智能交通路径诱导方法＊

文孟飞，彭 军，刘伟荣，李 冲，张晓勇

（中南大学 信息科学与工程学院，湖南 长沙 410075）

当前，缓解城市交通拥堵问题的方法主要有两种：一是加大城市路网建设力度，提升路网吞吐量；二是发展智能交通系统（Intelligent Transportation Systems，ITS），提高道路运行效率.针对各大城市越来越有限的土地资源，以智能学习的方式，优化城市路网运营和管理，显然是一种最实际的解决方案.动态交通路径诱导系统是ITS的一个重要方向，对城市交通路网管理的效果愈发显著.它采用检测技术、计算机技术、网络技术等高新手段，基于实时交通信息采集、处理与传输，通过中心式、分布式等多种诱导方式，为驾驶员提供交通事件、行程时间和优化路径等动态信息，可引导驾驶员避开拥挤走最佳行驶路线，从而实现路网交通流的均衡动态分配，有效缓解交通拥挤.高效的路径选择算法是动态交通路径诱导系统的关键技术.从本质上来说，路径选择算法需集中式收集整个路网信息，选择恰当的交通流函数，通过高效的算法对路网进行快速更新，动态地找寻满足一定约束条件的最优路径.构建路网模型，选择高效算法，动态地选择源节点到目的节点的最优路径，从局部来说对驾驶员路径选择作出最优安排，从总体上说可优化城市路网流量的均衡分配，解决路网的拥堵问题.

动态路径诱导在ITS、通信系统和机器人等人工智能方面应用广泛.若城市路网是静态网络，路段信息不变且可知，则很容易通过全局规划找寻一条从源状态到最终状态的最佳路径.但实际情况却是，交通信息时刻都在变化，环境信息动态改变，实际行驶过程中的路网情况和初始情况差异很大，此时需不断更新路网信息，实时找寻源状态节点到最终状态节点的动态最优路径.一些学者已研究了在动态环境情况下找寻最优路径的方案和算法思想[1－4］，局部重规划就是其中一种关键算法，能有效地实现动态环境下的路径诱导，将历史数据保留，通过算法重用，减少了重新获取整个路网信息的工作量.

经典的路径诱导方案通常只针对单个因素进行优化，但实际上现实问题往往由多方面因素相互制约，单个因素很难正确描述，因而路径诱导往往需对多个因素进行同时处理和优化，即多目标路径诱导.作为人工智能的关键方法，启发式搜索已应用于多目标路径诱导研究，很多学者进行了相关研究.Stewart和White将A＊算法延伸到多个优化变量，并利用启发式搜索解决路径诱导，从而提出了多目标启发式搜索模型[5］；Dasgupta改进了多目标启发式搜索，引入非单调的启发信息用于解决VLSI设计难题[6］；Mandow针对节点难以扩展问题，将路径扩展引入多目标启发式搜索，提高了搜索算法的准确性[6－7］；Harikumar和 Dasgupta总结了深度优先搜索算法在多目标路径诱导上的应用[8－10］.通过对多个变量进行优化，多数状态空间搜索规划器改进了智能规划技术[11－13］.

文献[14－16］将增量搜索思想引入路径诱导局部重规划.在许多相似度较高的多目标优化问题中，环境信息只是局部变化，若重新进行全局规划会带来不必要的计算复杂度，若能够对历史信息重用，则可提高算法效率.本文提出了一种当检测到环境信息动态改变时，怎样实时选择最优路径以实现全局最优规划的路径诱导方案，先由当前的静态路网信息利用启发式搜索算法作全局规划，找寻最短路径；车辆行进过程中，一旦路网信息变化，就需不断更新历史信息，在之前规划的信息前提上再作增量搜索，减少计算复杂度，提高算法效率，从而利用动态局部重规划找寻目前状态到最终状态的最优路径方案.

1 构建路网模型

城市交通网络错综复杂，但都是由单个交叉路口构成的，可利用图论法抽象为点线的网格拓扑，用点代表平面交叉口，用线代表路段，如图1所示.这样路网可以抽象为由节点集合、弧段集合和路权集合等构成的几何赋权图.

图1 带路径权重的多交叉口路网图论模型Fig.1 Multi－intersection graph model with path weights

G＝（N，A，C）表示整个网络的状态空间图，N＝ ｛Ni，i＝1，2，…，9｝为交叉口集合，A＝ ｛Ai，i＝1，2，…，11｝为任意两相邻交叉口之间的路段，C（Np，Nq）为路段权重，是指由交叉口Np到交叉口Nq所需代价值.本文中G为无向图，C（Np，Nq）＝C（Nq，Np）.

实际路网中单个优化变量很难准确描述复杂的交通网络，本文用多目标优化变量来精确描述交通状态.多目标优化变量存储在向量m中，m的维数反映优化变量个数，每一个优化变量都反映单因素的优化目标.路段的权重则是由多个优化变量共同作用的结果.若考虑该路段车辆排队长度PA，t，车流阻塞密度KA和路段通行能力MA这3个多优化目标，则：

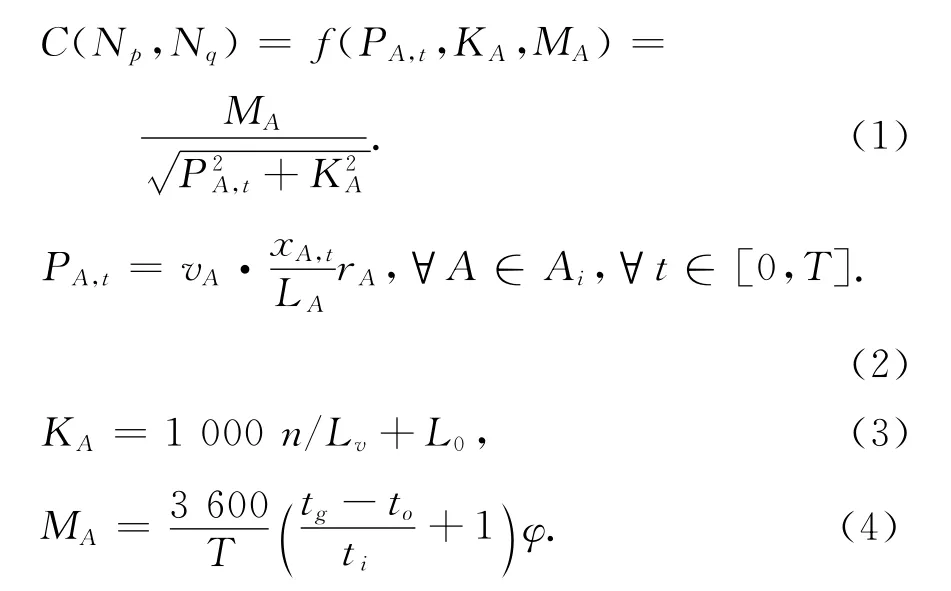
式（2）中：vA为路段A上的车辆自由流密度，xA，t为路段A在t时刻的交通负荷，LA为路段A的长度，rA为路段A下游交叉口路口红灯的相位时长，T为信号周期.式（3）中n为单方向机动车的车道数量，Lv为阻塞情况下平均车距，Lo为平均车身长度.式（4）中tg表示该交叉口每个周期的路灯时间，to表示绿灯亮时，第一个通过停车线的车所消耗的时间，ti表示直行右转通过停车线所需的平均时间，φ为折扣系数，通常取0.9.

多目标路径诱导问题转换为数学模型由四元组〈G，Nstart，Ngoal，U〉来表示，Nstart∈N 为初始节点；Ngoal∈N为目标状态节点，U为多目标评价函数，即为所找路径d各路段多目标权重之和，如式（5）所示，按照搜索算法找出从Nstart到Ngoal最优路径.

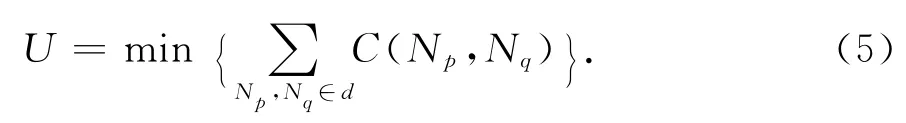
通过将实际交通路网抽象出来，以数学形式存储路网模型.首先根据启发式搜索算法找出从起始状态节点到目标状态节点的最优路径；当车辆在行驶过程中某些路段权重发生变化，若全局更新则会降低系统实时性，本文通过动态重规划算法对经过该路段的局部路径网络进行代价更新，从而可提高算法效率和系统实时性.

2 多目标启发式搜索算法

启发式搜索就是在搜索过程中对每一个搜索的状态到目标状态进行代价评估，选择最好的下一个状态直到目标状态，从而减少了无用的搜索，提高了算法效率.

多目标启发式搜索将多目标优化变量引入到路径权重中去，由权重函数C（Np，Nq）算出路段的综合权重来实现多目标问题的优化.

算法设计中除了考虑各路段权重时，还要给出从当前节点到达目的节点的评估值.算法过程中将目前搜索的各节点的所有未被搜索的路径保存在INIT表中，每一条路径d可由三元组（Nm，g（d），f（d））表示，U为多目标评价代价函数，根据多目标变量得出路径代价，END表记录当前找出来的解路径代价.其中g（d）表示从源节点到当前节点的代价和，f（d）表示当前节点到最终状态节点的评估代价，即启发函数，如式（6），取3个优化变量的历史平均值作为该路段的变量值，算出从当前节点到最终状态节点平均估计值，搜索主要以此信息提高效率.

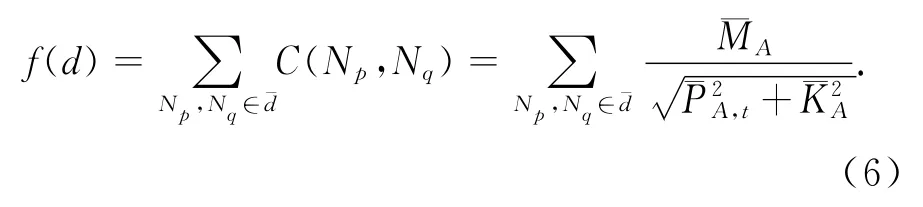
多目标启发式搜索算法 MHA（〈G，Nstart，Ngoal，U〉，INIT，END）.

该算法输入变量是〈G，Nstart，Ngoal，U〉，并初始化INIT表与END表，最后输出Nstart到Ngoal的最优路径.

1）查询INIT表，根据多目标代价评价函数U选择代价估值最小的dx路径扩展，dx代价由g（dx）表示；

2）在INIT表查询并删除dx的记录项（Nm，g（dx），f（dx）），然后将dx从Ho（m）移到Hc（m）.其中Ho（m）保存经Nm的所有未扩展的路径，Hc（m）保存经Nm的所有已扩展的路径；

3）若Nm＝Nstart，则找到一条解路径，去掉INIT表中小于g（dx）的与其有关的所有未搜索路径，并在END表中加入g（dx）；

4）若Nm≠Nstart，则查询未搜索的所有状态Nn，产生到达Nn的路径dy，且g（dy）＝g（dx）＋C（Nm，Nn）；

5）如果g（dy）小于Ho（n）∪Hc（n）中任意路径代价，则将dy插入Ho（n），并删除Ho（n）∪Hc（n）中所有小于dy的路径.计算路径dy的代价估值f（dy），若f（dy）小于 END 中任何解路径，则将（Nn，g（dy），f（dy））加入INIT 表且保存之前的关联代价值；

6）检测INIT表是否为零，若不为零则转到步1）；

7）输出搜索出的Nstart和Ngoal间的最优路径，并给出最小代价值.

启发式搜索算法应用到复杂交通网路，且当路况变化频繁时，启发式数量急剧增长，算法时间消耗较大，适应性降低.增量搜索算法能很好地利用路网变化的局部变化信息，避免全局更新，对提高算法的效率具有积极意义.

3 基于增量搜索交通动态路径诱导

城市复杂交通网络日益拥堵，动态交通诱导思想可以很好地改善交通状况.考虑城市交通环境时刻变化给算法效率带来的问题，可在之前已有的搜索信息上只对变化的部分进行局部动态重规划，从而提高算法效率.增量搜索算法可实现局部的动态重规划，来解决环境时刻变化问题.本文将增量搜索算法引入到启发式搜索算法，提出了动态多目标路径 诱 导 算 法 DMRGA（Dynamic Multi－objective Route Guidance Algorithm），该算法既保留了启发式搜索快速高效的特点，又能适应于复杂的动态网路环境，进行动态路径诱导.在本文提出的路网模型上，结合启发式搜索算法和增量搜索算法的思想，进行全局规划和动态局部重规划，很好地解决了实时找寻最优路径的问题，解决车辆动态路径诱导问题.

DMRGA算法分为两部分：全局规划及局部动态重规划.全局规划根据已知的静态城市网路信息找寻源状态到最终状态的最优路径；局部规划则是在路网环境信息动态变化时，先在局部做静态规划，然后在原有基础上作增量搜索，进行动态重规划，实时调整最优路径.当检测路网信息发生变化时，须马上作出响应，动态调整目前节点到最终节点的最优路径，以免造成不必要的延时，影响路网全局性能.

本节阐述的局部动态重规划是多目标路径诱导算法的关键算法，只对局部变化的信息实时更新，引入增量搜索算法动态调整路径.动态多目标路径诱导算法DMRGA算法如下.

动态多目标路径诱导算法DMRGA（G，Nstart，Ngoal，U）.

该算法输入变量 〈G，Nstart，Ngoal，U〉，输出源状态节点到最终状态节点间的最优路径

1）初始化.INIT ＝ （Ngoal，ggoal，fgoal），END 为空集；

2）全局规划.执行多目标启发式搜索过程MHA（〈G，Nstart，Ngoal，U〉，INIT，END），找 寻 源 状态到最终状态的最优路径集合，并选择其中一条；

3）沿着算法得出的路径行驶，若抵达最终状态，则输出该条搜索路径，跳到5）；若移动到某个节点Nchange时，其相邻节点Nv代价信息变化，跳到4）；

4）基于增量搜索的局部重规划：

Ⅰ 执行更新过程UDDATE（Nchange）；

ⅰ 更新Ho（Nchange）∪Hc（Nchange）中所有包括（Nchange，Nv）的路径；

ⅱ 令 END′＝Ho（Nchange）∪Hc（Nchange），Hc（Nchange）＝Ho（Nchange）∪Hc（Nchange），接下来并将Ho（Nchange）置为空集；

ⅲ对Ngoal扩展到Nchange过程中所有中间状态Nu的Ho（Nu）集合中所有路径代价gu，接着算出抵达Nchange节点的估计代价值fu，且END′中解路径均小于fu，则向INIT′插入记录（Nu，gu，fu）.

Ⅱ 执行多目标启发式搜索过程 MHA（〈G，Nchange，Ngoal，U〉，INIT′，END′），重新计算Nchange与目标状态Ngoal之间的最优路径集合；

Ⅲ 若成功到达目标节点，则转移到步骤5），否则跳到Ⅰ继续循环搜索，直至找到目标节点.

5）算法结束.

DMRGA根据已知的静态城市网路信息找寻源状态到最终状态的最优路径集合，并选择其中一条，即先做全局规划.Ho（m）∪Hc（m）保存了每一个搜索节点与最终目标节点间所有的的最优路径.

在向最终目标搜索移动过程中，若环境信息变化，则进行DMRGA算法第4步动态局部重规划，直至抵达最终节点.若检测到Nchange到Nv之间的路径代价发生变化，则对Ho（Nchange）∪Hc（Nchange）中经过（Nchange，Nv）的所有路径代价进行实时更新；当Nchange与Nv之间出现障碍物阻塞时，删除Ho（Nchange）∪Hc（Nchange）中所有经过（Nchange，Nv）的路径代价.算法动态更新后的Ho（Nchange）∪Hc（Nchange）既为重规划过程所要求解的局部最优路径，重新遍历Ngoal搜索到Nchange中所经过的节点Nu的所有未搜索的路径集合Ho（u），从而产生动态局部重规划的初始INIT表.在此INIT表基础上，以Ngoal为源状态节点，Nchange为最终状态节点进行逆向的启发式搜索，找寻新的源状态节点到最终状态节点间的最优路径集合.

全局规划是从最终状态节点向源状态节点进行搜索，然局部重规划则是从最终状态节点向发生变化的节点进行局部搜索，两次搜索算法相同但意义却不同.故局部动态重规划能很大程度上重用全局规划中各状态节点的Ho与Hc，以后的进一步重规划则是在先前规划基础上进行局部增量搜索，尽可能重用历史信息，提高算法效率.可被重用的历史信息有两类：1）初始INIT已提供所有状态节点的所有位扩展路径，而无需每次规划都扩展节点路径；2）由Ho（Nchange）∪Hc（Nchange）可以直接获得重规划过程的部分解路径，而不需要逐个求解.

4 仿真与分析

本仿真以VS2010作为开发平台，搭建实验平台，选择长沙市五一大道中段一段路网，提取出路网模型，验证基于增量搜索的启发式路径诱导方法的效率和实时性.

图2为选择的长沙市五一路中段某一道路，本文将交叉路口看作节点，各路段看作节点间的连线和权重，为了便于算法设计，将路网抽象如图3所示的标准网格型网络.图3中加深的N2号表示起点，加深的N17号为终点，本仿真是从N2寻找到达N17的最优路径.

图2 长沙市五一路中段道路Fig.2 Middle of Wuyi road in Changsha

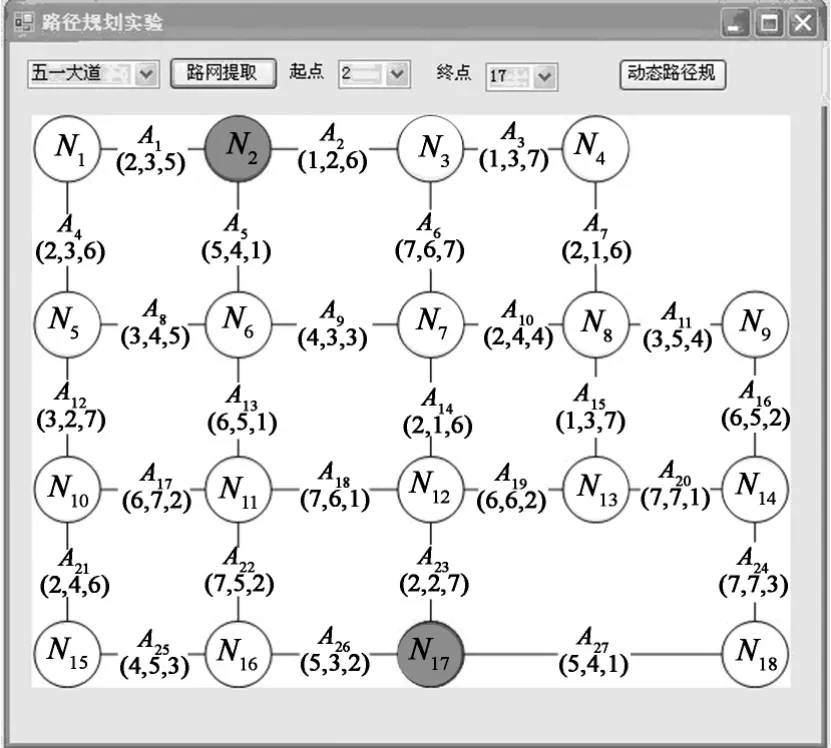
图3 长沙市五一路中段路网模型Fig.3 Model for middle of Wuyi road in Changsha

图4中权值加粗表示该路段状况实时变化，加粗箭头为选出的最优路径.提取出路网后，算法根据启发式搜索进行全局规划找出最优路径，如图5所示.随着车辆行驶到交叉口N6时，A9路段车流密度及延时明显增大，根据增量算法进行局部动态重规划，将经过该路段的路径代价进行局部更新，其他路径则不变，从而有效地提高了效率，此时选择A13路段前进.当到达N11时，A22路段明显得到改善，又进行动态重规划选择A22继续前进.车辆行驶过程所需时间代价表如表1所示.

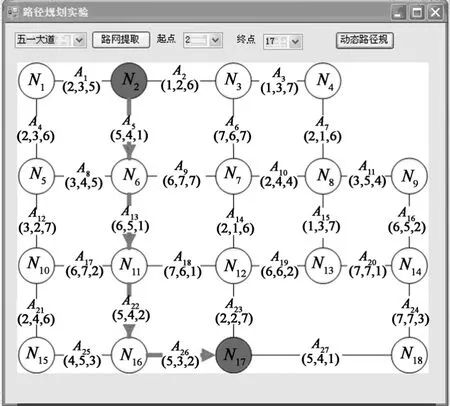
图4 局部动态重规划Fig.4 Local dynamic re－planning

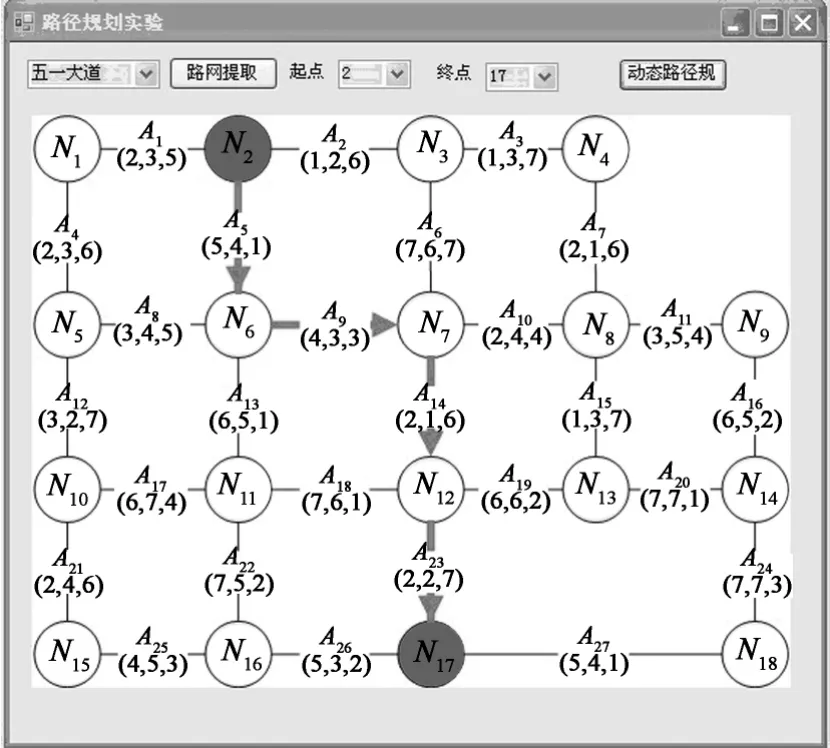
图5 全局规划路径Fig.5 Global path planning

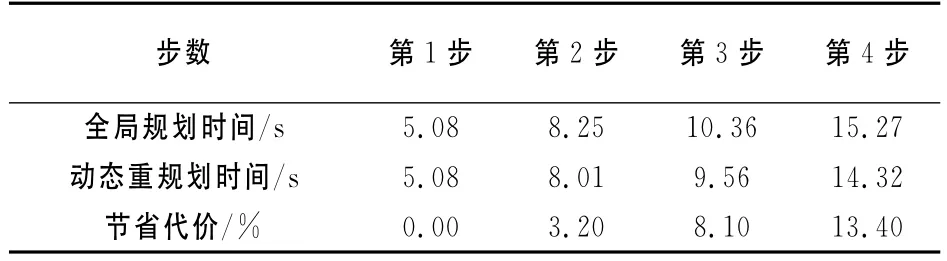
表1 全局规划和动态重规划时间比较表Tab.1 Global planning and dynamic re－planning time table

实验结果表明，车辆在行驶过程随着路网某路段权重的更新，其最优行驶路径也在不断更新，动态实时地调整行车路线，尽可能减少行车耗时.实验以一个小型的部分路网作为场景，可以扩大到整个路网，实时给出车辆优化路径.

5 结 论

本文针对时刻变化的路网信息，提出一种基于增量搜索的多目标路径诱导方法.该方法首先利用图论法将复杂路网抽象为点线的赋权图，引入多目标优化变量，建立路网模型.然后在启发式搜索基础上引入增量搜索，结合全局规划和局部动态重规划，实现车辆的动态路径诱导.首先进行全局规划，利用多目标启发式搜索算法找寻最优路径集合；当检测到环境信息变化时，进行动态局部重规划，在尽可能保留前次规划的基础上进行增量搜索，减少算法复杂度，提高效率，实时更新最优路径.最后仿真结果表明该方法能有效地实时解决复杂路网中车辆的动态路径诱导问题.

[1]ZHU Q B.Ants predictive algorithm for path planning of robot in a complex dynamic environment[J］.Chinese Journal of Computers，2005，28（11）：1898－1906.

[2]KOENIG S，LIKHACHEV M，FURCY D.Lifelong planning A＊[J］.Artificial Intelligence，2004，155（1/2）：93－146.

[3]YANG J，ZHANG M.A two－level path planning method for on－road autonomous driving[C］//2th International Conference on Intelligent System Design and Engineering Application，Sanya，China：2012：661－664.

[4]XI Y G，ZHANG C G.Rolling path planning of mobile robot in a kind of dynamic uncertain environment[J］.Acta Automatica Sinica，2002，28（2）：161－175.

[5]STEWART S B，WHITE C C.Multiobjective A＊[J］.Journal of the ACM，1991，38（4）：775－814.

[6]OLIVEIRA RIOS L H，CHAIMOWICZ L.A survey and classification of A＊based best－first heuristic search algorithms[C］//Advances in Artificial Intelligence－SBIA.Sao Bernardo do Campo，Brazil：2010：253－262.

[7]MANDOW L，PEREZ J L DE AL CRUZ.A new approach to multi－objective A＊search[C］//Proceedings of the 19th International Joint Conference on Artificial Intelligence.San Francisco，USA：2005：218－223.

[8]DASGUPTA P，CHAKRABARTI P P，DESAKAR S C.Multiobjective heuristic search[M］.Morgan Kaufman，1999.

[9]XU Y Y，YUE W Y.A generalized framework for BDD－based replanning A＊search[C］//Artifical Intelligences，Networking and Parallel/Distributed Computing.10th ACIN International Conference on Software Engineering.Daegu South Korea，2009：133－139.

[10］HARIKUMAR S，KUMAR S.Iterative deepening multiobjective A＊[J］.Information Processing Letters，1996，58（1）：11－15.

[11］REFANIDIS，VLAHAVAS I.Multiobjective heuristic statespace planning[J］.Artificial Intelligence，2003，145（1/2）：1－32.

[12］SO M B，KAMBHAMDATI S.Sapa：A multi－objective metric temporal planner[J］.Journal of Artificial Intelligence Research，2003，20：155－194.

[13］SVEN K，MAXIM L，LIU Y X，etal.Incremental heuristic search in AI[J］.AI Magazine，2004，25（2）：99－112.

[14］WEI W，OUYANG D T，LU N，etal.A multiobjective incremental heuristic search algorithm[J］.Journal of Jilin University：Science Edition，2009，47（4）：752－758.

[15］LU Y B，HUO X M，OKTAY A ，etal.Incremental multiscale search algorithm for dynamic path planning with low worst－case complexity[J］.IEEE Trannactionn on Systems，Man，and Cybernetics－part B：Cybernetics，2011，41（6）：1556－1569.

[16］SVEN K，SUN X X.Comparing real－time and incremental heuristic search for real－time situated agents[J］.Auton Agent Multi－Agent Syst，2009，18：313－341.