基于接触摩擦的变截面钢板弹簧悬架性能分析＊

周水庭，黄红武，付建朝，左 佳，向铁明

（1.湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082；2.厦门理工学院 机械与汽车工程学院，福建 厦门 361024；3.湖南易通汽车配件科技发展有限公司，湖南 长沙 410137）

钢板弹簧是汽车悬架中一种最常见的弹性元件.它是由若干片等宽但不等长（厚度可以相等，也可以不相等）的合金弹簧片组合而成的一根近似等强度的弹性梁，在悬架中兼作导向机构.常用的主要有两种类型，一种是片宽、片厚保持不变的传统多片钢板弹簧，另一种是等宽度、变厚度断面的变截面钢板弹簧.而少片变截面钢板弹簧是指由少片（1～4片）变截面的弹簧片构成的钢板弹簧[1］.长期的实践表明，少片簧利用变截面来保持等强度特性，使材料大为节省，质量大为减轻.据统计，若采用少片簧，在同样寿命的情况下，其质量约比多片簧减少40%～50%；同时又减少了片间摩擦，可改善行驶平顺性，故少片簧应用逐渐增多[2］.

通常情况下，当整车总布置的一系列参数确定之后，在少片变截面钢板弹簧悬架的设计选型中，其簧片数、长度、宽度、厚度、曲率半径、自由弧高和总成刚度等基本参数，就能随之得到.其中，各簧片及总成的曲率半径、自由弧高和总成刚度是板簧总成设计的主要参数，均由其预应力决定.因此，在少片变截面钢板弹簧悬架的设计中，簧片的预应力计算与刚度分析至关重要.

据统计，美国三大汽车公司1978年采用变截面钢板弹簧约占板簧总产量的60%.我国从20世纪80年代开始研制变截面钢板弹簧.由于在实际工况中，钢板弹簧往往同时存在着大应力和大变形，尤其是传统计算方法没有考虑片间接触摩擦等非线性因素，导致其计算精度受到严重影响，误差较大.本文考虑了片间实际存在的接触摩擦状况，对少片变截面钢板弹簧进行性能计算与分析，比传统方法更能反映钢板弹簧的实际工作情况.

1 基于接触摩擦的钢板弹簧悬架性能的计算理论

文献[3－8］表明：对于接触摩擦问题，一般将两个面的接触简化为由3个节点组成的接触对.基于接触摩擦的有限元方法对钢板弹簧悬架性能的计算和分析，实质上是对簧片进行虚拟装配，由于考虑了片间实际存在的接触摩擦，相比传统计算方法能更准确、真实地模拟簧片之间的非线性接触因素.

传统的整体有限元方程为：

添加摩擦接触单元后的钢板弹簧悬架整体有限元方程为：

式中：M为总体质量矩阵；D为所有等效节点位移组成的向量；K为总体刚度矩阵；Fc为所有等效接触节点摩擦力向量组成的向量；F为所有等效节点力向量组成的向量.

2 基于接触摩擦的少片变截面钢板弹簧有限元建模

钢板弹簧通常基于材料力学小挠度梁的线弹性理论进行传统分析，即采用简化力学模型.而本文应用Unigraphics软件，根据每片弹簧在自由状态下的自由弧高、曲率半径和三维尺寸，对每片弹簧进行装配前的参数化建模，然后对所建立的簧片进行初步装配[9］.输入不同的板簧参数，可以获得需要的板簧三维模型，这样可以大大节省建模时间.

本文有限元分析采用映射法划分网格，选用Solid45六面体单元.少片簧材料为60Si2Mn，在系统中杨氏模量设置为2.1×1010Pa，泊松比为0.3[10］.

由于自由簧片的实体形状不满足映射单元对划分实体形状的要求，所以必须先对少片变截面钢板弹簧进行分块.分块情况如图1所示.首先，在有限元分析软件中导入已经分块的实体模型；然后，对实体模型划分单元，各接触面上的网格密度设置为完全相同；接下来，对分块的有限元模型采用合并的方法，把所有在同一位置的节点合并为一点，将它们重新组合在一起.这样就把各分块合并为一个整体了[11].

图1 少片变截面钢板弹簧的分块Fig.1 Block of taper leaf spring

相接触的两簧片之间定义一个接触对.由于该钢板弹簧由4片变截面的弹簧片构成，因此整个板簧总成共定义3个接触对，每一个接触对均由一个接触面和一个目标面组成，定义凸面为接触面，凹面为目标面.图2为板簧接触对的示意图.直接在接触面上添加接触单元，使接触面承受接触力.本文考虑的是接触摩擦，按簧片在良好的润滑状况下计算，摩擦因数设置为0.2[12］.在这里，钢板弹簧是采用非线性有限元分析，接触刚度与板簧的形状和尺寸等参数有关，所以要不断调试才能得到与该板簧相匹配的接触刚度值.其值设置太大将导致结果不收敛，太小则会降低计算精度.但当接触渗透量达到下极限时，接触刚度值应定义得相对较小.

图2 接触面单元Fig.2 Contact surface element

在本文研究中，先用较小的刚度值进行试运算.当计算结果收敛时，若程序提示渗透过多，则加大刚度值；当程序提示需经更多的迭代步骤才能完成残余应力和位移的收敛时，则应降低刚度值.反复调试，直至达到计算精度的要求[13］.经调试，本次计算接触刚度值确定为0.001.

3 仿真计算

3.1 少片变截面钢板弹簧装配仿真

拧紧钢板弹簧的中心螺栓和螺母，用特殊夹具支撑夹紧各簧片，各簧片（除夹具约束处外）在装配过程中均保持自由变形.在板簧的装配仿真中，模型按下面的方法进行处理：对中间各簧片，施加中央螺栓孔处的径向约束和宽度方向上的约束；定义最上片的底面中央垂直位移为0，最下片顶面中央有垂直方向的位移，自由状态下各簧片之间间隙的总和即为位移的大小.各簧片两端不施加任何约束，让其自由变形.

图3和图4分别为装配等效应力云图和装配后其中一片的预应力云图.

图3 虚拟装配预应力云图Fig.3 Virtual assemble prestress distribution

图4 某片预应力云图Fig.4 Prestress distribution of individual piece

表1给出了用传统的“共同曲率法”求出的理论预应力值和用有限元进行装配仿真得出的预应力值.从表中可以看出，使用传统的计算方法与基于接触摩擦的有限元方法计算出来的预应力值的变化趋势是一致的.同时可以发现，由于传统理论计算的前提是装配后所有簧片是相互紧贴的，而且不考虑接触摩擦，但事实上簧片间的间隙和接触摩擦始终是存在的，因此相对传统计算方法，有限元装配仿真中得出的簧片变形和预应力均相对偏小.

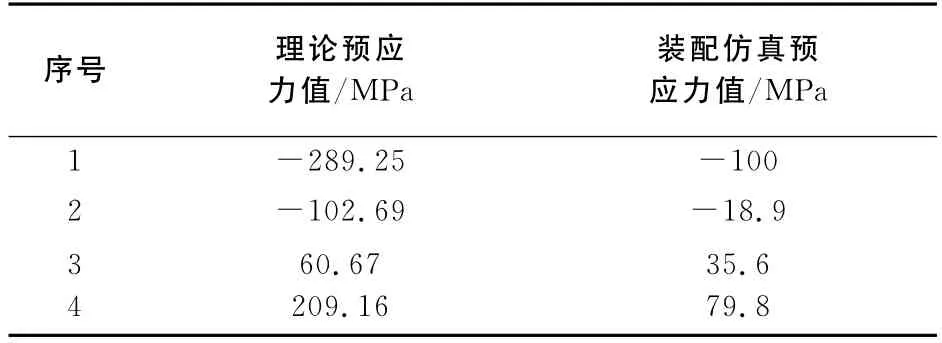
表1 用传统方法计算的理论预应力值与装配仿真预应力值的比较Tab.1 Comparison of the prestress which calculated with traditional way and by virtual assembly

3.2 少片变截面钢板弹簧的刚度仿真分析与试验对比

钢板弹簧总成的刚度仿真过程分成7个载荷步，从空载逐级加载至静载的1.5倍.

为确保计算结果收敛，设置Newton Raphson Options时，先选择Full，然后选择UNSYM.并选择SPARSE SOLVER作为求解器.图5为第7个载荷步的应力云图.

从图5可知，在第1、第4簧片与夹板接触处附近应力最大，最大值约为700MPa，仍然在材料的许用应力范围内.有限元仿真表明，少片变截面钢板弹簧符合强度要求.

从表2仿真计算结果可知，在逐级加载过程中，钢板弹簧的挠度和负载变化基本呈线性规律；静态刚度保持在400N/mm左右，且变化不大，符合该型号钢板弹簧的设计要求390±30N/mm.

图5 第7次加载应力云图Fig.5 The seventh loading stress nephogram

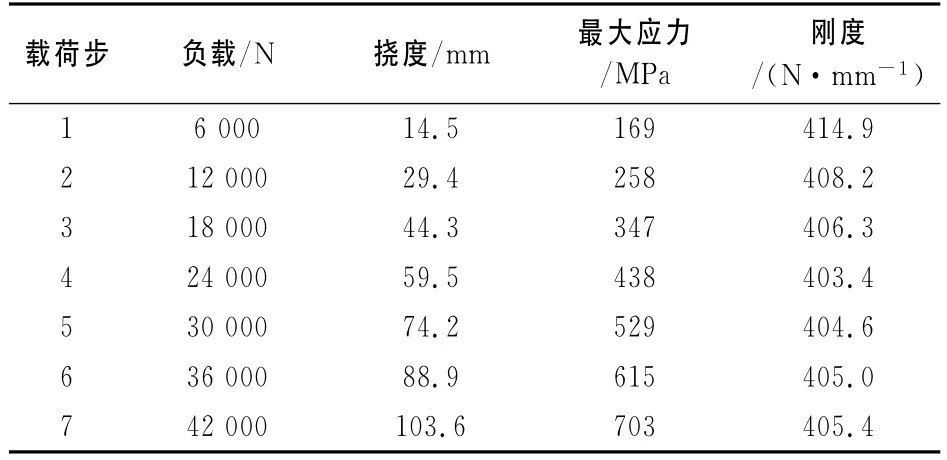
表2 钢板弹簧悬架仿真计算结果Tab.2 The simulating calculation results of taper leaf spring suspension

根据GB/T 19844－2005，设计弹簧特性试验台如图6所示.该装置采用滑动销轴和夹紧机构对钢板弹簧进行夹紧支承.试验中，逐级对钢板弹簧进行加载和卸载，测试钢板弹簧的静态刚度、静载弧高和空载弧高等参数.这样，通过试验就可以验证仿真与试验结果的一致性.试验结果如表3所示.

图6 弹簧特性试验台Fig.6 The test bed of spring properties

从表3可以发现，静态刚度、静载弧高和空载弧高3个参数的仿真计算值与试验测试值的相对误差分别为5.58%，9.58%和1.03%，结果非常接近.产生相对误差的原因是：金属材料在实际测试过程中由于经过喷丸、热处理等工艺处理，晶状结构因相互挤压而产生变形，材料性能表现为各向异性，而仿真计算中材料性能设置为各向同性.

表3 仿真与试验结果的对比Tab.3 Comparison of the simulation and test results

3.3 少片变截面钢板弹簧的阻尼特性分析

基于接触摩擦，首先通过对钢板弹簧总成进行静载压缩仿真，计算出钢板弹簧总成在整个压缩过程中的变形能E1；然后拆散钢板弹簧总成，对每一簧片进行静载压缩仿真，算出每一簧片的变形能Epi（i＝1，2，3，4），所有簧片的变形能之和即为没有考虑摩擦状态的钢板弹簧变形能；两次仿真变形能的差值即为摩擦力所做的负功Eξ.

根据振动学理论：

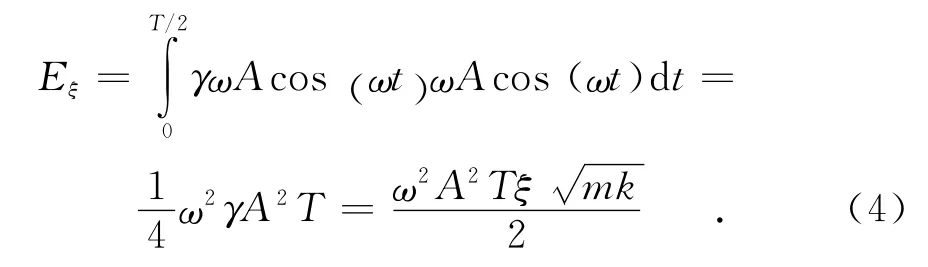
式中：ω为驱动力圆频率；γ为阻尼系数；A为振幅；T为振动周期；ξ为阻尼比；m为板簧质量；k为板簧刚度.

最后可求出板簧总成的阻尼比为0.010 6.其阻尼比可用来评价阻尼的大小或振动衰减的快慢程度.通过有目的地改变板簧片间摩擦垫片的材料，就改变了板簧片间的摩擦因数，从而改变悬架系统的阻尼，可为整个悬架系统的减震器设计提供有益的参考.

4 结 论

1）簧片的预应力决定了簧片自由曲率半径和总成的自由弧高.与传统计算方法相比，基于有限元接触分析的计算方法能更全面合理地对少片变截面钢板弹簧悬架进行应力、刚度和阻尼特性分析，得到与实际更吻合的计算结果.

2）通过基于接触摩擦的有限元法计算出钢板弹簧悬架的阻尼，再配合确定减震器参数，可设计出理想的悬架系统.

3）使用基于接触摩擦的有限元方法完全可以代替传统计算方法计算悬架的性能，得到更接近实际的悬架特性.这样就可以缩短悬架总成的设计开发周期.

[1]林小瑛.少片不等长变截面钢板弹簧的优化设计[J］.福州大学学报，2001，29（1）：56－59.LIN Xiao－ying.An optimum design of the few different lengths of taper leaf spring[J］.Journal of Fuzhou University，2001，29（1）：56－59.（In Chinese）

[2]张洪欣.汽车设计[M］.2版.北京：机械工业出版社，1996：149－151.ZHANG Hong－xin.Automotive design[M］.2nd ed.China Machine Press，1996：149－151.（In Chinese）

[3]WRIGGERS P，VAN T V，STEIN E.Finite element formulation of large deformation impact－contact problems with friction[J］.Computer Structure，1990，37（3）：319－331.

[4]BERTSEKAS D P.Constrained optimization and lagrange multiplier methods[M］.New York：Academic Press，1984：325－327.

[5]WOO K L，THOMAS T R.Contact of rough surfaces：a review of experimental work[J］.1980，58（2）：331－340.

[6]WRIGGERS P.Computational contact mechanics[M］.New York：John Wiley ＆ Sons Ltd，2002：320－323.

[7]唐应时，陈明媚，潘佳炜，等.基于接触摩擦的多片式钢板弹簧悬架预应力的计算[J］.湖南大学学报：自然科学版，2009，36（4）：29－33.TANG Ying－shi，CHEN Ming－mei，PAN Jia－wei，etal.Computation of the prestress of multi－leaf spring based on FEM with contact friction[J］.Journal of Hunan University：Natural Sciences，2009，36（4）：29－33.（In Chinese）

[8]刘桂荣，QUEK S S.有限元法实用教程[M］.长沙：湖南大学出版社，2004：31－32.LIU Gui－rong，QUEK S S.The finite element method：apractical course[M］.Changsha：Hunan University Press，2004：31－32.（In Chinese）

[9]唐应时，占良胜，方其让，等.基于动态仿真的副变速器箱体有限元分析[J］.中南大学学报：自然科学版，2006，37（4）：769－774.TANG Ying－shi，ZHAN Liang－sheng，FANG Qi－rang，etal.Finite element analysis of sub－transmission case based on dynamic analysis[J］.Journal of Central South University：Natural Science，2006，37（4）：769－774.（In Chinese）

[10］唐应时，柴天，和进军，等.基于接触摩擦的少片变截面钢板弹簧的刚度分析[J］.中南大学学报：自然科学版，2009，40（3）：694－698.TANG Ying－shi，CHAI Tian，HE Jin－jun，etal.Analysis of stiffness of taper leaf spring based on contact friction[J］.Journal of Central South University：Natural Science，2009，40（3）：694－698.（In Chinese）

[11］张建乔，刘永红，吕广忠.基于参数化模型特征的有限元网格划分方法研究[J］.制造业自动化，2005，27（9）：33－35.ZHANG Jian－qiao，LIU Yong－hong，LV Guang－zhong.The FEM mesh generation method based on characteristic manufacturing automation[J］.Manufacturing Automation，2005，27（9）：33－35.（In Chinese）

[12］李轶石.基于有限元的某多片钢板弹簧性能仿真研究[D］.长沙：湖南大学机械与运载工程学院，2007：36－37.LI Yi－shi.Character simulation rearch of multi－leaf spring based on FEM[D］.Changsha：College of Mechanical and Vehicle Engineering，Hunan University，2007：36－37.（In Chinese）

[13］谷安涛.应用CAE技术进行钢板弹簧精确设计[J］.汽车工程，2002，24（1）：73－75.GU An－tao.Precise design for laminated spring using CAE[J］.Automotive Engineers，2002，24（1）：73－75.（In Chinese）