一类积分-微分方程解的有界性与渐近性

李文娟，马 勇

（1.赤峰学院数学与统计学院；2.中国人民解放军93088部队，内蒙古赤峰024000）

一类积分-微分方程解的有界性与渐近性

李文娟1，马 勇2

（1.赤峰学院数学与统计学院；2.中国人民解放军93088部队，内蒙古赤峰024000）

主要研究了一类具有偏差变元的高阶积分微分方程解的有界性与渐近性.给出了这类方程解有界的充分条件，所得结果包含并改进了已有的一些结果.

有界性；渐近性；积分微分方程

关于积分微分方程解的有界性与渐近性，目前已有许多结果[1-7].文[1]研究了方程的解的有界性与渐近性.

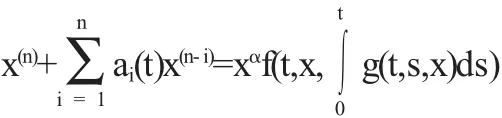
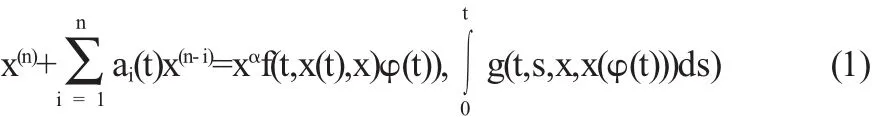
本文的主要目的是利用不等式研究一类更为广泛的具有偏差变元的积分微分方程的解的有界性与渐近性.其中R3→R是连续函数.α＞0是常数,且最终为正.为定义在[γ,0]上的可微函数，方程在区间R+上的初值问题的解即是存在一函数x(t),满足：

(1)x(0+)=θ(0-),x'(0+)=θ'(0-),…x(n-1)(0+)=θ(n-1)(0-)

(2)x(j)(t)=θ(j)(t),t∈[γ,0),j=0,1,…,n-1,

(3)x(i)(t),1≤i≤n,在R+上存在且x(t)满足方程.

本文假设满足这些条件的解存在.

方程(1)对应的齐次方程的n个线性无关解ø1，ø2，…，øn.定义ø=c1ø1+c2ø2+…+cnøn其中c1,…cn是常数.

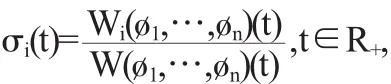
其中Wi(ø1,…,øn)是Wornskian行列式W(ø1,…,øn)中第列被(0,0,…,0,1)代替得到.

1 积分不等式

引理1[2]u(t),f(t),g(t),h(t)是R+上的非负连续函数,c＞0且为常数.p＞0,p≠1是常数.若

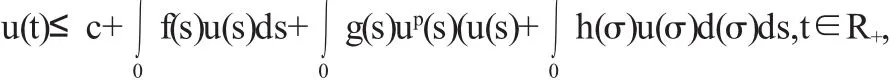
(1)如果0＜p＜1,则

(2)如果1＜p＜∞,则

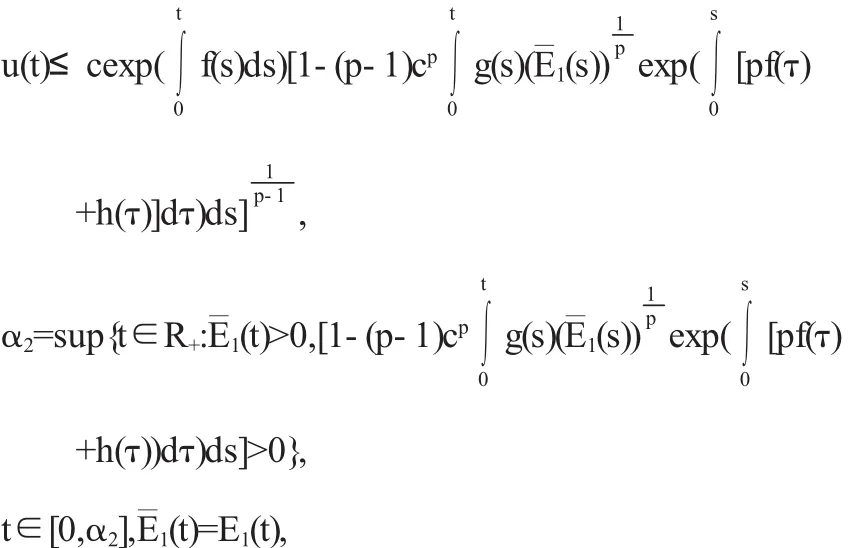
2 接的有界性与渐近性

情况1当0＜α＜1时有

定理1方程(1)满足∶

其中c＞0,M＞0是常数.s-r≤φ(s)≤s,φ'(s)＞0,且φ(s)最终为正.

(2)函数f(t,u1,u2,u3),g(t,s,u1,u2)满足

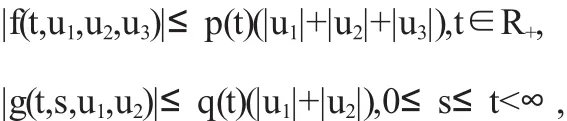
其中p(t),q(s)∶R+→R+是连续函数.

(3)如果

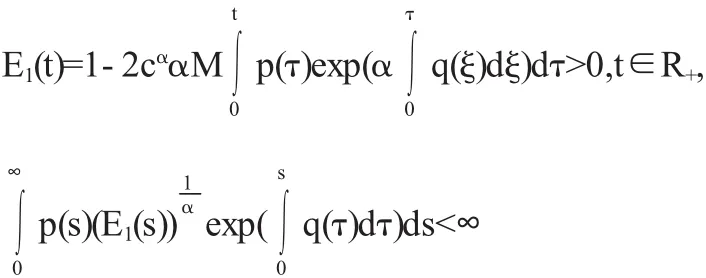
则方程(1)的所有解于R+上有界.

证明由常数变易法.方程(1)的任意解可表示为

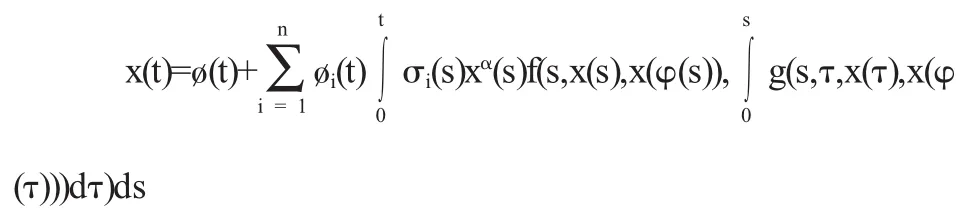
其中ø=c1ø1+c2ø2+…+cnøn,c1,…cn是常数,ø1,ø2,…,øn是方程(2)的n个线性无关解.由题设知

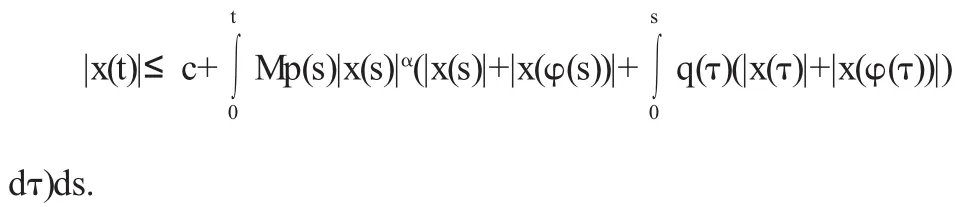
令w(t)=max{|x(t)|,|x(φ(t))}.因上式的右端单调不减,则

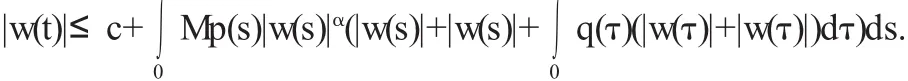
由上式知

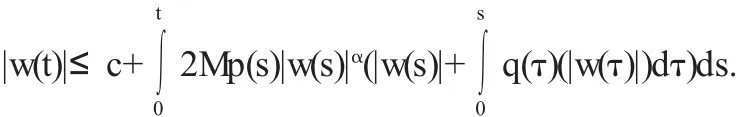
由引理得

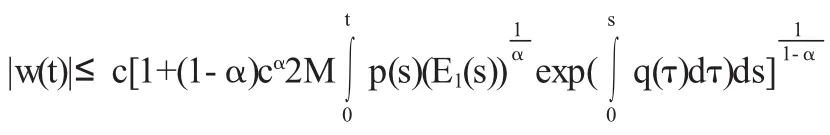
由于|x(t)|≤|w(t)|,且由上式及题设知w(t)有界.得方程(1)的解有界.

注1在定理1中取φ(s)=s,则定理1包含了文[1]中的一条定理.

定理2方程(1)满足∶

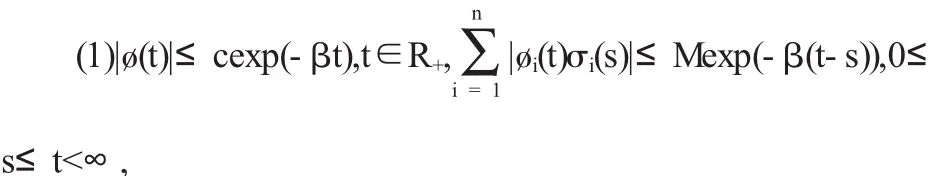
其中c＞0,M＞0,β＞0是常数.s-r≤φ(s)≤s,φ'(s)＞0,且φ(s)最终为正.

(2)函数f(t,u1,u2,u3),g(t,s,u1,u2)满足

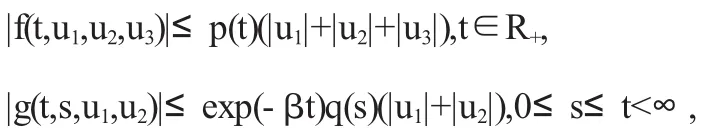
其中p(t),q(s)∶R+→R+是连续函数.

(3)如果

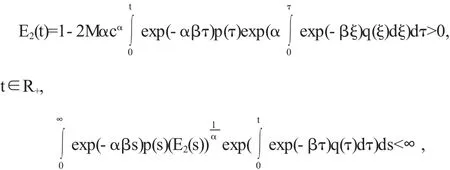
则方程(1)的一切解x(t)→0,→∞.

证明由常数变易法.方程(1)的任意解可表示为

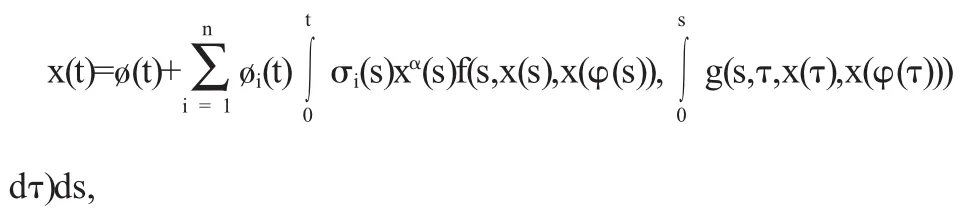
其中ø=c1ø1+c2ø2+…+cnøn,c1,…cn是常数,ø1,ø2,…,øn是方程(2)的n个线性无关解.由题设知

上式可被写为

令w(t)=exp(βτ)max{|x(t),|x(φ(t)|}.因上式的右端单调不减,则

由引理得

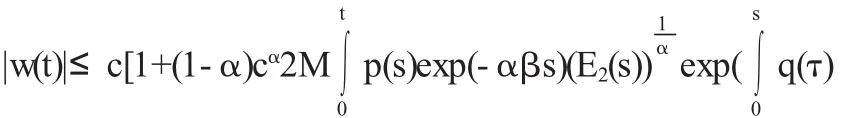
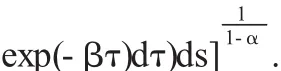
由上式及题设知w(t)有界且|x(t)|≤|w(t)|exp(-βt),得到x (t)→,t→∞.

注2在定理2中取φ(s)=s,则定理2包含了文[1]中的一条定理.

情况2当α＞1时有

定理3方程(1)满足∶

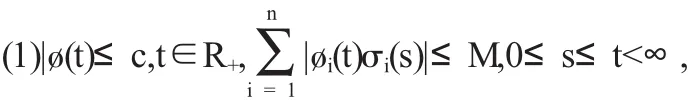
其中c＞0,M＞0是常数.s-r≤φ(s)≤s,φ'(s),且φ(s)最终为正.

(2)函数f(t,u1,u2,u3),g(t,s,u1,u2)满足

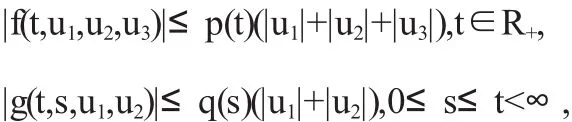
其中p(t),q(s)∶R+→R+是连续函数.

(3)如果

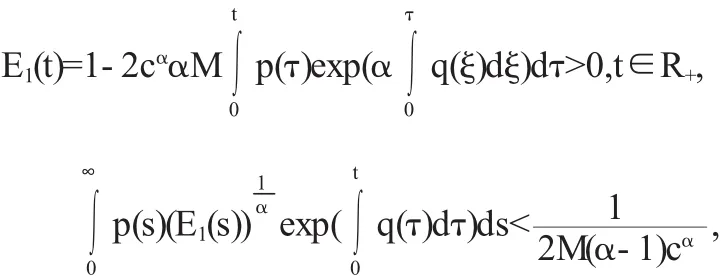
则方程(1)的所有解于R+上有界.

证明类似定理1的证明.

定理4方程(1)满足∶

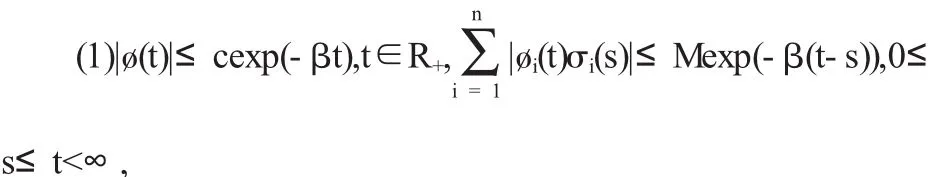
其中c＞0,M＞0,β＞0是常数.s-r≤φ(s)≤s,φ'(s)＞0,且φ(s)最终为正.

(2)函数f(t,u1,u2,u3),g(t,s,u1,u2)满足

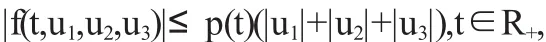
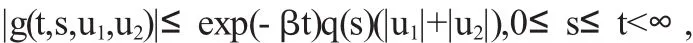
其中p(t),q(s)∶R+→R+是连续函数.

(3)如果

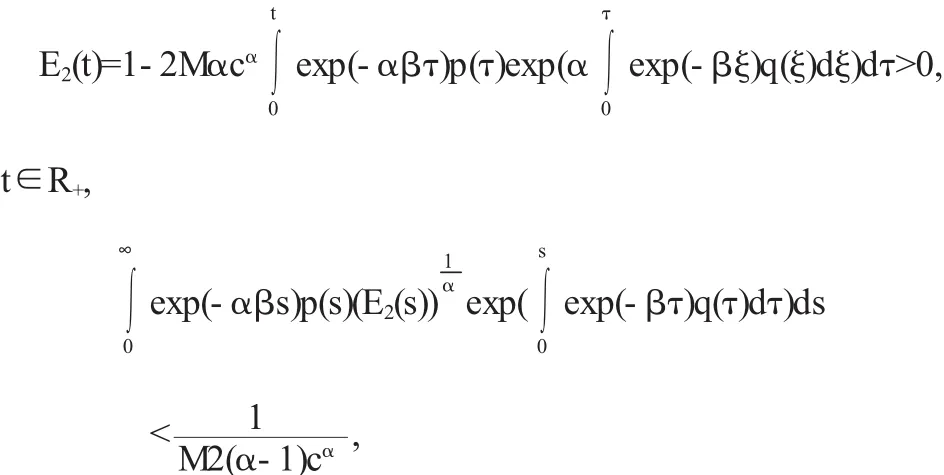
则方程(1)的一切解x(t)→0,t→∞.

证明类似定理2的证明.——————————

〔1〕Pachpatte,B.G.,On a class of nonlinear nth order integrodifferential equations[J].J.M.A.C.T,1976,9:37-45.

〔2〕Pachpatte,B G.,On some new integral inequalities for differential and integral equations[J].J.Math.physical Sci. 1976,10,101-116.

〔3〕孟凡伟.二阶非线性积分-微分方程解的有界性[J].滨州师专学报,2001,17(4):5-8.

〔4〕许志宏,孟凡伟.一类具有偏差变元的二阶非线性积分微分方程解的有界性[J].聊城大学学报:自然科学版,2005,18 (1):16-19.

〔5〕纪德红，孟凡伟.一类高阶非线性具有偏差变元的微分方程解的有界性[J].工程数学学报，2006，23(6):1064-1067.

〔6〕李文娟.二阶非齐次泛函微分方程解的有界性[J].赤峰学院学报，2009,25（2）:1-4.

〔7〕李文娟，斯力更.一类二阶积分微分方程解的有界性与渐近性[J].2009,38（3）:243-248.

O175

A

1673-260X（2013）01-0004-03