典型二阶系统控制器设计

哈斯花

（赤峰工业职业技术学院，内蒙古赤峰024000）

典型二阶系统控制器设计

哈斯花

（赤峰工业职业技术学院，内蒙古赤峰024000）

主要研究了典型二阶系统控制器的设计方法.首先分析了二阶系统的建模过程，然后设计了PID控制器，给出了校正后单位阶跃响应图、校正后伯德图、Simulink仿真、最后给出了稳定性分析.经过分析可知，系统在没有经过校正前不满足要求，经过PID校正后系统的稳态误差为零，调整时间缩短，反应速度快，具有较强的抗干扰性和较好的鲁棒性.

二阶系统数学模型；PID控制器；系统稳定性

1 建立系统的数学模型

设输出气压为p(t)，输出位移x(t),有牛顿第二定理可得：

pA-kx(t)-bv=(M+m)a

代入数据M=0.08kg，m=0.02kg，k=4N/m，b=0. 04Ns/m，A=0.002m并整理后得：

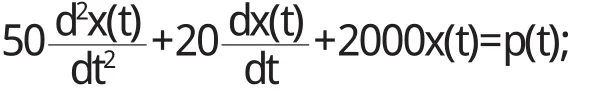
对上式做拉氏变换可求出系统的开环传递函数：

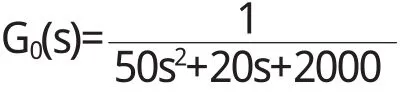
进一步可求的系统的闭环传递函数：

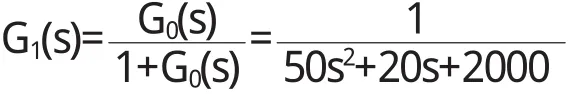
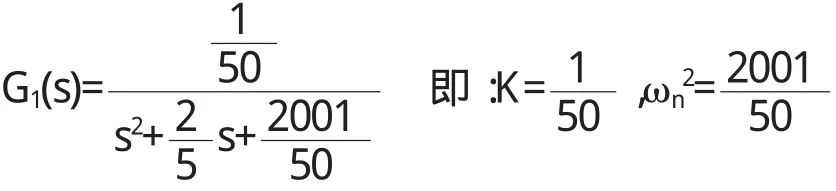
求系统的闭环极点:

闭环传递函数的特征方程：

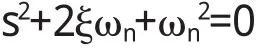
可求出闭环极点

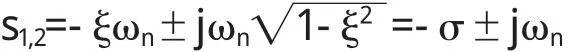
当输入为单位阶跃函数时即r(t)=1(t),R(s)=1/2特征值为是特征根的实部，代入数据可得σ=0.2，-σ=-0.2是特征根的虚部，称为阻尼振荡频率.代入数据可得：ωd=6.33

s 1 到s 平面坐标原点的距离为ωn

s 1 向量与s 平面负实轴的夹角β 称为阻尼角.

β=arccosξ β=88°（已接近零阻尼状态）

-σ=-0.2 ωd=6.33 β=88°绘制复平面二阶系统闭环极点分布图：

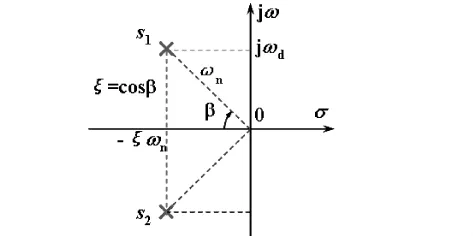
如图所示两个共轭复根在s平面的左半平面虽然接近虚轴但由上图可知系统仍是稳定的.

系统的输入为单位阶跃函数

代入公式得当r(t)=1(t)时，稳态误差ess=1

综上所述原系统不满足性能要求

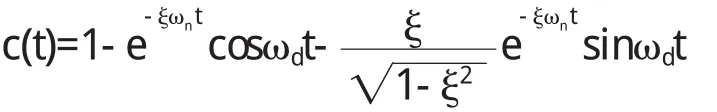
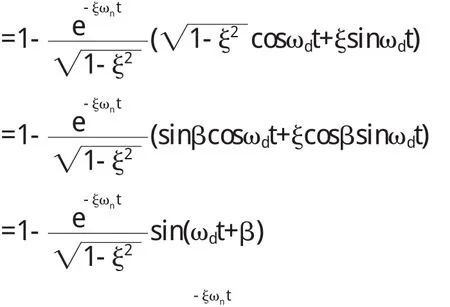
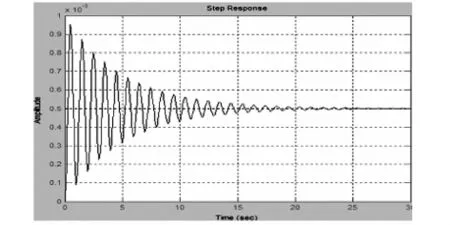
原系统的阶跃响应曲线如下图：

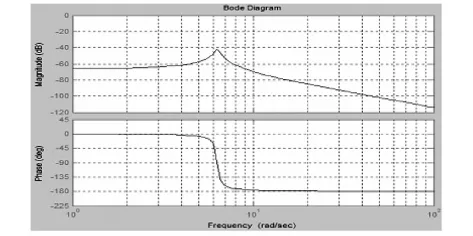
原系统的伯德图如下：

由性能要求可以反求出系统最终的阻尼比和角频率：

2 设计控制器

原系统的阻尼比为0.03已接近零阻尼状态，所以需要通过设计控制器增加系统的阻尼比.故在控制器中加入比例微分环节，微分控制规律能反应输入信号的变化趋势，产生有效的早期修正信号，以增加系统的阻尼程度，从而改善系统的稳定性.原系统为0型系统，在输入为r(t)=1(t)时存在稳态误差，需要在控制器中加入积分环节，PI控制器相当于在系统中增加了一个位于原点的开环极点，同时也增加了个位于S左半平面的开环零点.增加的负实零点用来提高系统的阻尼程度，缓和PI控制器极点对系统稳定性产生的不利影响.位于原点的极点可以提高系统的型别，即将系统提高到Ⅰ型，以消除或减小系统的稳态误差，改善系统的稳态性能.单位反馈系统框图如下：

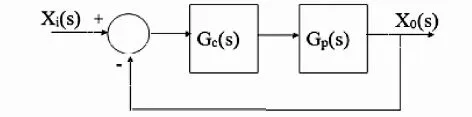
PID校正计算：

PID控制器的传递函数Gc(s)=Kp[1+1/Tis+Tds]其中Kp为可调比例系数

Ti为可调积分时间常数Td为微分时间常数

校正后系统的开环传递函数为

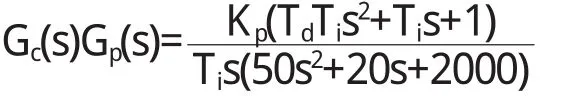
单位负反馈闭环传递函数为：

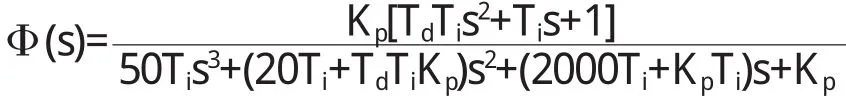
假设得到的闭环传递函数三阶特征多项式可分解为

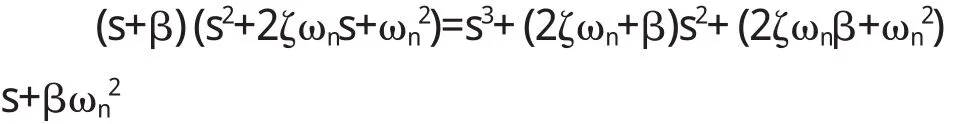
令对应项系数相等，有

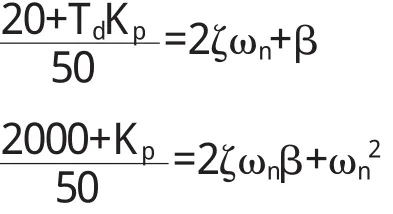
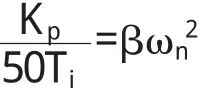
可求得PID校正所需的参数Kp，Ti，Td

校正后系统的特征多项式：

特征多项式不缺项，列出劳斯表：

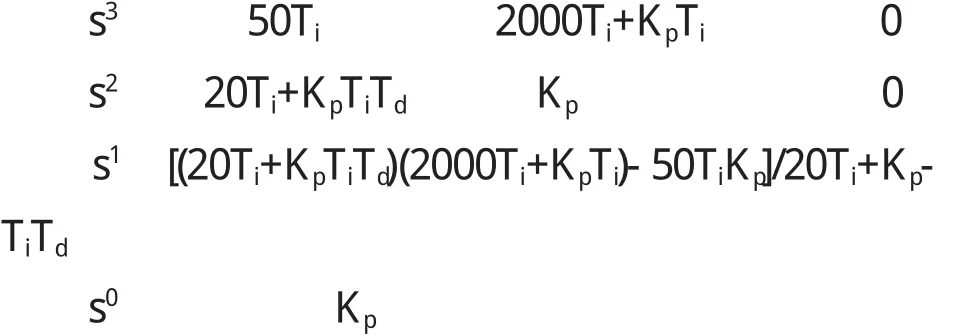
由劳斯表可知系统稳定.

校正后单位阶跃响应如下图：

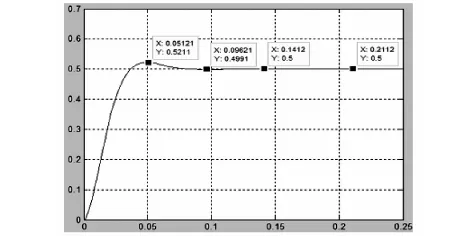
校正后得伯德图如下图：

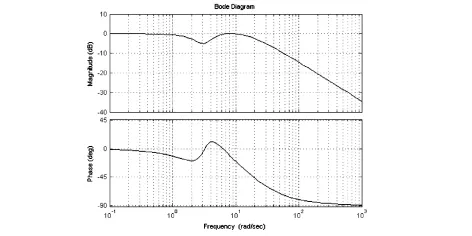
由校正后的时域响应曲线和频域响应伯德图可知：校正后系统的性能指标满足要求.所以控制器的传递函数为Gc(s)

3 Simulink仿真

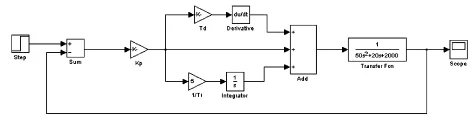
4 稳定性分析

质量变化对系统的稳定性影响较大，但质量的变化，系统仍能在调整时间内并在允许误差范围内达到稳定，系统的鲁棒性较好.现在令在1s时系统受到一个脉冲信号的干扰，经实验证明，此时系统的响应曲线较平滑且系统最终能回到平衡位置，达到稳态，抗干扰能力强.

5 结论

经过分析可知，系统在没有经过校正前不满足要求，经过PID校正后系统的稳态差为零，调整时间缩短，反应速度快，具有较强的抗干扰性和较好的鲁棒性.这说明P控制器实质上是一个具有可调增益的放大器.在信号变换过程中，P控制器只改变信号的增益而不影响其相位.在串联校正中，加大控制器增益KP，可以提高系统的开环增益，减小系统稳态误差，从而提高系统的控制精度，但系统的相对稳定性，甚至可能造成闭环系统不稳定，因此在系统校正设计中，不能单独使用比例控制规律；微分控制可以增大系统的阻尼，使阶跃响应的超调量下降，调节时间缩短，且不影响常值稳态误差及系统的自然频率.由于采用微分控制后，允许选取较高的开环增益，因此在保证一定的动态性能条件下，可以减小稳态误差，但是微分控制器只对动态过程起作用，而对稳态过程没有影响，且对系统噪声非常敏感，所以，单一的D控制器在任何情况下都不宜与被控对象串联起来单独使用；而I控制器可提高系统的型别，有利于系统稳态性能的提高，但积分控制使系统增加了一个位于原点的开环极点，使信号产生了900的相角迟后，于系统稳定性不利，因此，在控制系统的校正设计中，通常不宜采用单一的I控制器.所以系统采用了PID控制器，达到了系统的控制要求.

〔1〕夏德钤，翁贻方.自动控制理论[M].北京：机械工业出版社，2007.

〔2〕杨叔子，杨克冲，等.机械工程控制基础[M].武汉：华中科技大学出版社，2005.

〔3〕薛安克，彭冬亮，等.自动控制原理[M].西安：西安电子科技大学出版社，2004.

〔4〕葛哲学，等.精通matlab[M].北京：电子工业出版社，2008.

TP273+.4

A

1673-260X（2013）01-0031-03