卡尔曼与粒子滤波在GPS多径估计中的应用研究

胡永昌

（西北工业大学 电子信息学院，陕西 西安 710072）

卡尔曼与粒子滤波在GPS多径估计中的应用研究

胡永昌

（西北工业大学 电子信息学院，陕西 西安 710072）

在多径环境下，GPS接收机码跟踪环的相关峰会产生严重的畸形。 为了最大程度的削弱多径效应，多径估计技术可以提供直射信号和反射信号的码偏分布，从而可以进一步根据码偏分布减少多径效应的干扰。基于MEDLL的码环设计，本文增加了自适应滤波模块去提高估计精度.。 我们使用GPS中频接收机采集实际信号，分析对比了卡尔曼滤波和粒子滤波在GPS多径估计中的性能。 结果发现，粒子滤波有很好的估计精度和抗噪性能，但耗费较大的计算量；卡拉曼滤波可以快速的进行数据处理，其抗噪性能相比之下大大降低。

GPS接收机；多径估计；MEDLL；卡尔曼滤波；粒子滤波

随着对全球卫星定位系统（GPS）精度需求的不断提高，GPS信号的多径效应逐渐成为GPS接收机设计的问题之一[1]。 多径效应是指GPS接收机在除了接收到直射信号以外，它还接收到了多份反射路径的信号。 多路径信号相对于直射信号在幅度上有衰减，而且由于传播的延迟，在相位上会有明显的变化。 由于多径信号是直射信号与多条路径信号的综合，所以多径效应会导致接收机C/A码解调时的自相关函数出现明显的畸形，从而极大地影响接收机的精度。

为了抑制多路径效应，我们主要可以从天线抑制和接收机的数字信号处理两个方面入手[2]。从天线抑制方面上说，大致有4种方法：1）用特殊的天线设计去抑制和抵消多径信号，如扼流圈天线（choke-ring）和右旋极化天线（RHCP）；2）利用多天线阵列接收信号，然后利用多天线的天空的多样性进行多路径抑制；3）精心的天线选址，从而尽量避免多径环境；4）通过移动天线同时长时间观察信号，测量信号变化从而消除反射信号。 从接收机的数字信号处理来说，主要是根据直射信号和多路径信号的特性，在接收机的设计上进行抑制多径效应，例如窄相关接收机（narrow-correlator），strobe接收机等等。而为了进一步估计多径信号，Richard D.J.提出MEDLL（multipath estimating delay lock loop）的多径估计相关机设计[3]。在此基础上，刘亚欢等给出了相关机的线性模型，并用最大似然估计给出了GPS的多径估计[4]。

由于多径信号相对于直射信号总是延迟，并且主要体现的码片的偏移上。 所以本文基于MEDLL的设计模型添加了自适性滤波模块去进行多径估计，此外刘亚欢等给出了相关机的线性模型分析，我们分别利用了卡尔曼滤波和粒子滤波处理多径估计信号。 我们首先测试两者在只有直射信号下的抗噪能力，然后利用GPS中频接收机采集了实际的信号分析和对比两者的多径估计效果。 结果表明卡尔曼滤波可以更快速估计，但是抗噪性能相比粒子滤波较弱，粒子滤波可以很好的处理搞噪声的信号，但是需要耗费大量计算时间。

1 GPS信号多径模型

1.1 多径信号的数学模型

接收的信号r（t）中存在多种不同多径信号，我们假设有m路多径信号，第j路信号（j=0表示直射信号）的幅度aj，信号延迟τj，信号相位θj与其它路都有所不同。 所以多径信号一般可以用如下公式表示为：

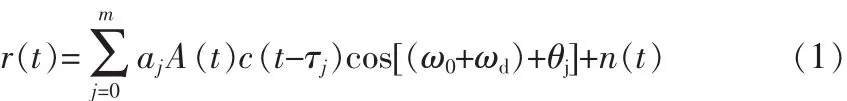
式中：A（t） 为调制信息；c（·）为扩频码；ω0、ωd分别为载波标称频率和多普勒频移；n（t）为输入的高斯白噪声。

1.2 相关积分累加输出模型

接收信号经过载波跟踪环路的载波剥离后，与多路本地产生码相干积分进行多径估计。 因为C/A码信号的调制信息周期为20 ms，而相干积分累加时间一般为1 ms，所以我们认为在相干积分累加时间内A（t）是不变的，笔者设之为1。我们认为本地相干码的码相位分别为，δ0，δ1…δn，并且认为载波环路完全跟踪，所以接收信号与其进行相干积分累加后的输出可以用以下公式表示：

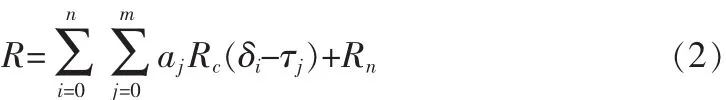
式中：RC（·）为扩频码的自相关函数；Rn为通过积分累加器后的噪声。 用矩阵形式表示出来如下：

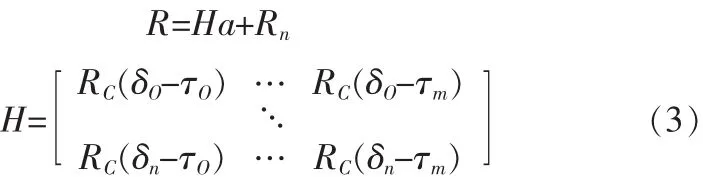
1.3 相关输出噪声

高斯白噪声通过积分累加器可以近似成为一个过低通滤波器的过程。所以在码相位为δn处，噪声的相关输出为：

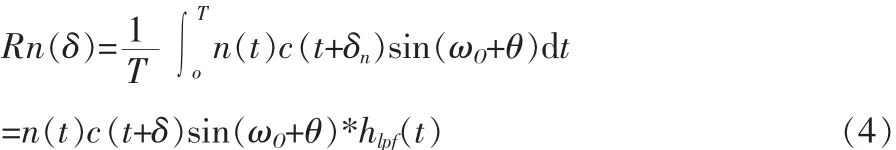
式中：n（t）为无穷带高斯白噪声，其单边带的功率谱为N0；hlpf（t）为积分累加滤波器的脉冲响应。其噪声的相关输出为一个单边带功率为N0，带宽为 [－BW，BW]的高斯噪声，其中BW=1/T，T为相关积分时间。噪声向量的协方差矩阵于是如下：

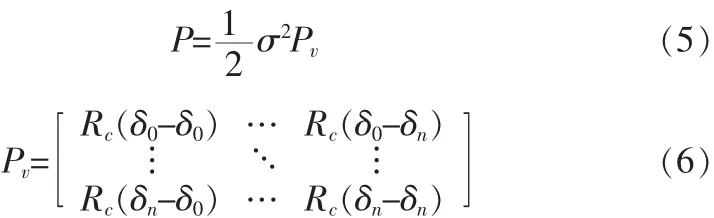
式中：σ2为码相位差为0时的噪声方差，即单点噪声方差。

2 GPS多径估计接收机设计

Richard D.J.提出的MEDLL的多径信号估计做法把信号估计和环路设计结合在一起，他用多路不同相位的本机扩频码与接收信号进行相关积分累加，其输出根据信号扩频码和本地扩频码之间码相位差可以在此扩频码的自相关函数上输出相应的信号幅值。如图1所示，接收信号进过载波剥离后，分别与码相位分别为δ0，δ1…δn的本地码进行相关积分累加。由于多径信号的多变性和接收环境的高噪声性，在MEDLL的基础上添加了自适应滤波模块。模块中的滤波器我们分别采用了卡尔曼滤波和粒子滤波，并对其进行分析对比。

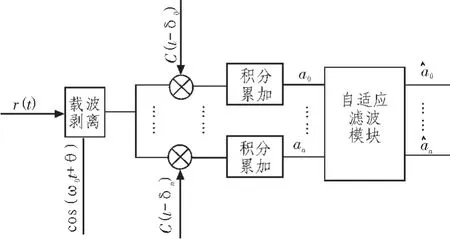
图1 GPS自适应多径估计接收机设计Fig.1 Structure diagram of GPS self-adaptive multipath estimator

3 自适应滤波算法

3.1 动态系统模型

我们已经知道了积分相关累加输出结果的矩阵形式，为了构造自适应滤波的观测模型和转移状态模型，我们用=（x0k，x1k，…，xmk）表示在 k 时刻用来拟合真实相关峰的估计输出相关峰值。所以线性观测模型和转移状态模型如下：

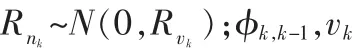
3.2 卡拉曼滤波

卡尔曼滤波基于动态系统模型是高斯分布，其滤波过程主要分两个阶段：预测和更新[5]。在预测阶段，滤波器根据上一状态的估计做出对当前状态的估计。在更新阶段，滤波器利用当前状态的观测值去优化在预测阶段获得的预测值，以获得一个更精确的新的估计值。根据已知的线性观测模型和转移状态模型，可以分别构建出预测过程和更新过程。在预测过程中，滤波器不仅预测当前状态，而且给出了当前预测估计的协方差矩阵，公式如下：

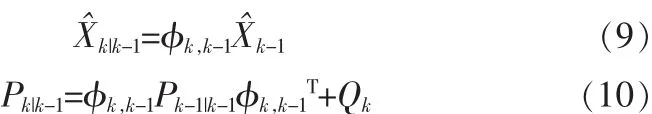
式中Pk|k－1为误差的相关矩阵。在更新过程中，滤波器根据当前预测值，计算出最优的卡尔曼增益Kk，然后用其修正当前预测值从而得到更精确的估计值，同时更新协方差矩阵。更新方程如下：

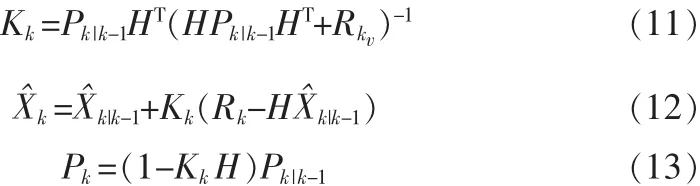
卡尔曼滤波假设动态系统模型服从高斯过程，但是由于实际环境的多变性，如多径信号在没有直射路径的情况下服从瑞利分布，在有直射路径的情况下服从莱斯分布，所以需要一个能准确描述多变的动态系统模型分布做出估计的算法。

3.3 粒子滤波

粒子滤波是一种基于蒙塔卡罗方法和递推贝叶斯估计得统计滤波方法，它依据大数定理采用蒙塔卡罗方法来求解贝叶斯估计中的积分运算[6]。它通过在传递样本集合和相应的重要性权重来进行估计，这些样本称为粒子，N为样本数。粒子滤波在重要性函数上采样得到相应的重要性权重，然后根据量测不断调整粒子的重要性权重和位置，从而进一步通过调整后的粒子信息修正经验条件分布。在过程中，有可能出现大量粒子只具有很小的权值，算法不能充分表达所期望的经验条件分布，这就是退化现象，于是我们需要进行重采样。粒子滤波的具体实现步骤如下：

1）初始化。初始化样本集。

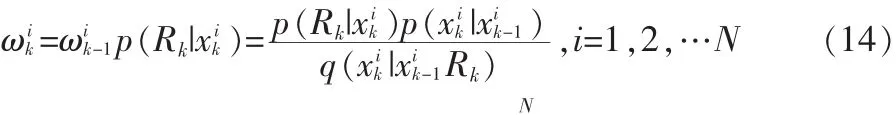
4）输出。

5）判断是否结束，若是则退出算法，若否则返回2）。

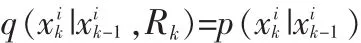
4 数据分析与对比

我们先用MATLAB仿真模拟了在只有直射信号下但存在不同程度噪声的多径估计效果。我们分别提高了观测噪声和过程噪声，观察两种滤波器对其的性能。然后利用卫星查询软件orbitron观察26号卫星轨道，选取合适地址用NEWS TAR210M GPS中频采集器采集实际信号进行多径估计处理。

4.1 MATLAB仿真

仿真中我们假设只有直射路径，并且对估计的相关峰等进行归一化，笔者设置时间步进为100，粒子滤波的样本数为100，改变观测噪声和过程噪声，观察2种滤波在拟合相关峰时的抗噪性。卡尔曼滤波的平均计算时间为0.259 4，而粒子滤波由于需要大量采样，其平均计算时间为0.344 2。

1）当观测噪声方差为0.01和转移噪声方差为0.000 1时，仿真结果1如图2所示。图2（a）为卡尔曼滤波的结果，右边为粒子滤波的结果，由上往下结果依次为未加滤波的实际相关峰，滤波后拟合的相关峰和估计的码偏幅值。可以看见在没有滤波的情况下实际的相关峰产生了小幅的畸变，加入滤波之后相关峰得到修正。对比两者，粒子滤波更精确的修正了相关峰。观察估计的码偏幅值，由于噪声在0.2码偏处卡尔曼滤波有较大的误差。

图2 仿真结果1Fig.2 Results of simulation one

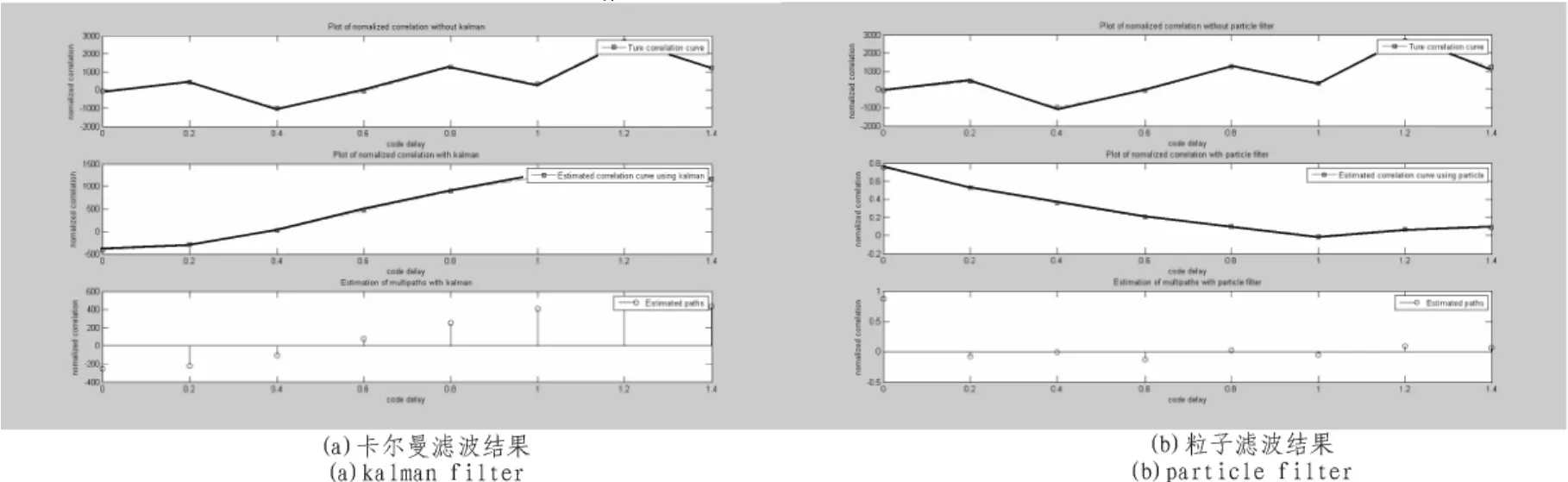
图3 仿真结果2Fig.3 Results of simulation two

2）加大观测噪声方差为1 000 000，并且保持转移噪声方差不变为0.000 1时，仿真结果2如图3所示。在较大的观测噪声情况下，没有滤波的情况下实际的相关峰产生了巨大的畸变，卡尔曼滤波也不再能正确修正相关峰。但是观察粒子滤波，由于大量的粒子采样修正条件经验分布，粒子滤波仍然可以很好的修正和保护相关峰。

3）笔者在保持观测噪声方差不变为0.01，但是提高转移噪声方差为0.01时，仿真结果3如图4所示 。提高转移噪声，发现两者都产生很严重的畸形，结果表明转移噪声对卡尔曼滤波和粒子滤波都有很明显的影响。但是在实际的GPS多径估计中，经过本地码解扩以后转移噪声不会对系统状态有太大影响，基本可以忽略不计。

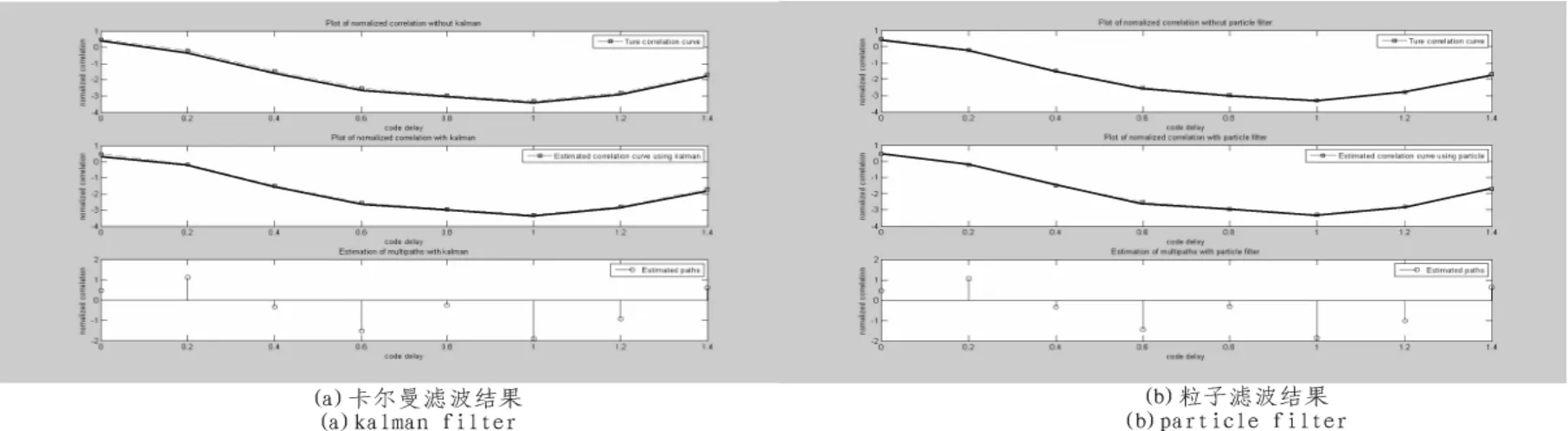
图4 仿真结果3Fig.4 Results of simulation three

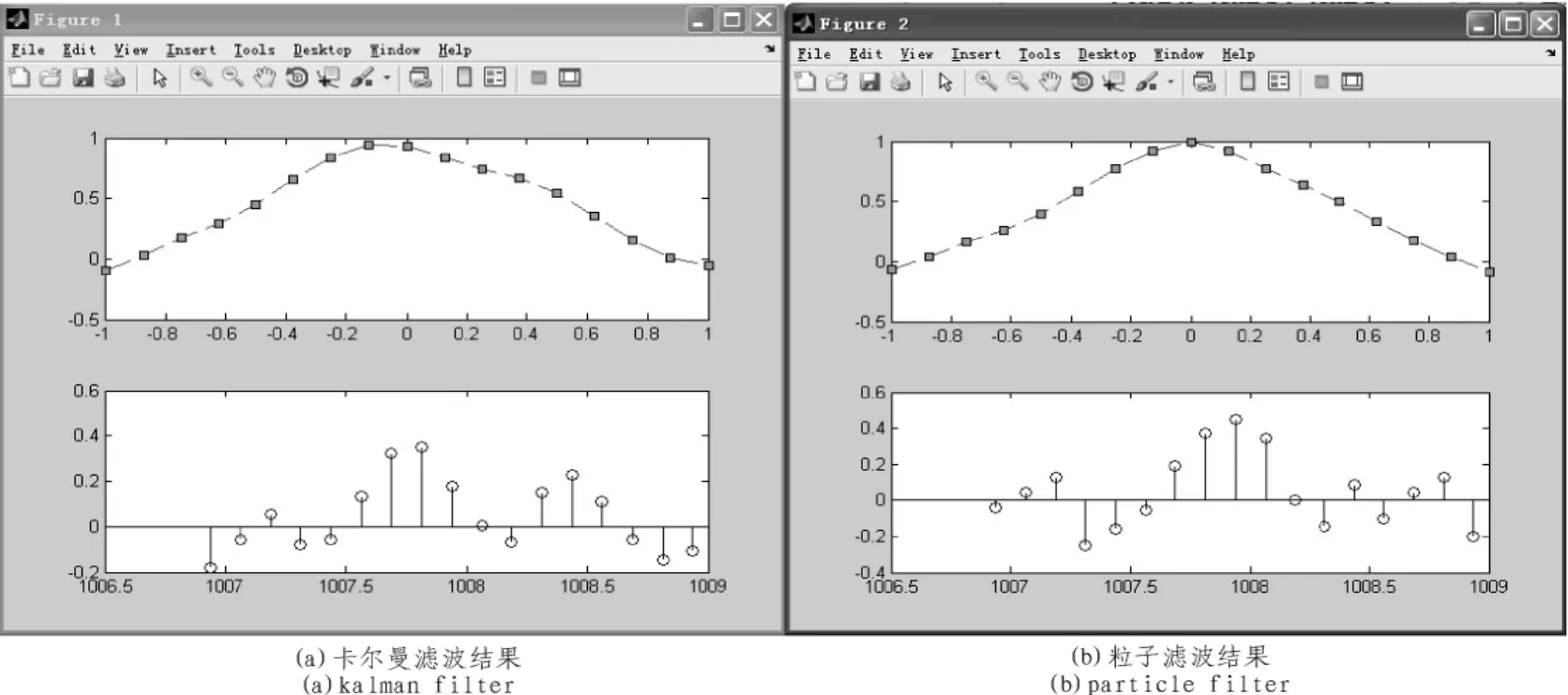
图5 实际GPS信号的多径估计结果Fig.5 Multipath-estimation result from real GPS signal

4.2 实际信号测试

利用NEWSTAR210M GPS中频采集器采集26号卫星信号。实际卫星分析结果为：码偏在1 007.9；多普勒频移为3.25 kHz。我们对其信号进行多径处理，图5给出了2种方法的对比图，图5（a）为卡拉曼滤波的结果，图 5（b）为粒子滤波的结果，由上往下依次为多径估计后的归一化的相关峰和多径码偏的幅值分布。可以看到两者方法显示的最大峰值都在1007.9码偏处，在1008.5出卡尔曼滤波有较大的多径影响。观测拟合的归一化相关峰，粒子滤波的相关峰更为偏向于标准三角形。

5 结 论

文中在MEDLL的基础上添加自适应滤波模块去进行GPS接收机的多径估计，分析和对比了卡尔曼滤波和粒子滤波在多径估计中的性能，并且采集了实际信号进行测试。发

现卡尔曼滤波相比粒子滤波运算速度更快，然而抗观测噪声的性能相比粒子滤波较为差。两种滤波方法面对状态转移噪声的时候，表现的十分脆弱，但是实际环境中状态转移噪声可以忽略不计。在实际信号测试中，卡尔曼滤波和粒子滤波都可以很好的估计出多径信号的码偏幅值分布，但是相比之下，粒子滤波能更好的修正拟合的相关峰。

[1]Kos T.Effects of multipath reception on GPS positioning performance[C]//ELMAR，2010 PROCEEDINGS．Zadar，2010:399-3402.

[2]Lawrence R W.Conquering multipath:the gps accuracy battle[J].GPS World，1997，8（4）:59-65.

[3]VAN N J.The multipath estimating delay lock loop[C]//Spread Spectrum Techniques and Applications，1992:39-342.

[4]刘亚欢，田宇，李国通．基于最大似然估计的GPS多径估计[J]．宇航学报，2009，30（4）：1466-1471．

LIU Ya-huan，TIAN Yu，LI Guo-tong.GPS multipath estimation based on maximum likelihood estimation[J].Journal of Astronautics，2009，30（4）:1466-1471.

[5]Welch G，Bishop G.An introduction to the kalman filter，897831[R].Chapel Hill，NC，USA，1995.

[6]Van T H，Bell K.A tutorial on particle filters for online Nonlinear/NonGaussian bayesian tracking [C]//Bayesian Bounds for Parameter Estimation and Nonli Wiley-IEEE Press，2007:723-737.

Performance of GPS multipath-estimator based on Kalman and particle filter

HU Yong-chang
（School of Electronics and Information， Northwestern Polytechnical University， Xi’an 710072， China）

Under the multipath environment，the cross-correlation function of GPS receiver in code tracking will be impacted significantly.In order to minimize this multipath effect at utmost，GPS multipath-estimator is able to provide the estimation of signals code phase of both direct and reflected path which can further be used to mitigate errors caused by multipath effect.Based on the multipath estimating delay lock loop （MEDLL）， this paper utilizes and adds the adaptive-filter to improve the accuracy.The GPS base-band signal receiver seizes the real GPS signals which are used to analyze and compare the performance of kalman filter and particle filter in GPS multipath-estimator.The results denote the particle filter performs better in accuracy and anti-noise in cost of tremendous compute amount， while kalman filter fast-processes the data， but suffer a heavy impact from noise.

GPS receiver； multipath-estimator； MEDLL； Kalman filter； particle filter

TP228.4

A

1674－6236（2013）04-0061-04

2012-10-25稿件编号201210165

胡永昌（1988—），男，陕西西安人，硕士。研究方向：卫星通信导航与测控、多媒体通信与信息处理。