插值FFT和滑动DTFT的科氏流量计信号处理方法

易 鹏，涂亚庆，杨辉跃

后勤工程学院 信息工程系，重庆 410311

插值FFT和滑动DTFT的科氏流量计信号处理方法

易 鹏，涂亚庆，杨辉跃

后勤工程学院 信息工程系，重庆 410311

1 引言

科氏流量计（Coriolis Mass Flowmeter，CMF）是一种基于科里奥利原理的直接式质量流量计，具有测量精度高、可测流体范围广、稳定性好、量程比大等特点，已在石油、化工、医药等行业得到广泛应用，是当前发展迅速、应用广泛、研究较多的测量仪表之一。图1为U型管科氏流量计结构。

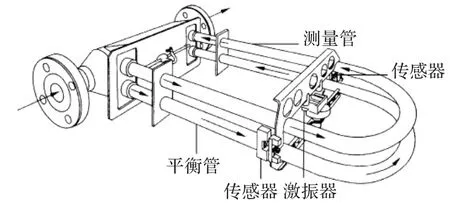
图1 科氏流量计结构图

科氏流量计通过测量一次仪表中两路磁电传感器输出的同频正弦信号的频率和相位差来计算时间差，进而求出质量流量，其信号处理方法是决定测量精度的关键因素之一。实际的科氏流量计信号，由于受到环境以及管内流体流速、密度和流体脉动等因素变化的影响[1]，频率、幅值和相位随时间变化。这些给科氏流量计的信号处理带来了困难，尤其是在空管中批料的开始和结束、多相流、非均匀流体等特殊的过程条件下，测量精度下降较大[2]。科氏流量计信号处理方法的优劣对于科氏流量计的测量精度及应用性能具有关键影响。

为提高测量精度，国内外的相关研究机构和公司纷纷将各种数字信号处理方法应用于科氏流量计的二次仪表，包括自适应陷波器、离散频谱校正、希尔伯特变换等方法[3-6]。这些研究成果有的忽略了各种流速条件下信号的时变特性，将科氏流量计信号处理过于简单，导致抗噪性能差，不能实时精确估计信号的频率和相位差；有的成果虽提高了计算精度，但算法过于复杂，计算量大，计算效率低，难以实现科氏流量计的实时流量测量。

本文根据科氏流量计实测信号特点，提出一种基于插值FFT的离散频谱校正方法求取信号频率，然后采用计及负频率的改进滑动DTFT方法求取相位差的科氏流量计数字信号处理方法，并进行了实验验证。

2 方法阐述

2.1 插值FFT的频谱校正频率估计

近年来对于科氏流量计频率估计的研究主要集中在陷波器方向上[3，5-8]。本文认为陷波器方法存在诸多缺陷：科氏流量计信号的频率由驱动其振动的激振器决定；通过分析采集到的科氏流量计实测信号得知，其频率虽随流量变化有小幅度变动，但非常之小，在1‰以内；所以在一定工作时间段内，可近似看作是固定频率的信号，而陷波器虽然能够跟踪频率的变化，但跟踪存在迟滞，且其误差往往超过1‰，尤其是在长时间的跟踪上，其陷波频率与真实信号的频率存在较大差距。由于科氏流量计信号频率受流体流量变化影响小，科氏流量计信号频率估计方法应着力于提高其计算精度和运算效率。鉴于此，本文提出采用基于插值FFT的频谱校正法用于科氏流量计信号的频率估计。

基于FFT频率估计的原理是通过快速傅里叶变换得到信号的离散频谱，求出其在最大谱线处的对应的频率，该频率即是信号频率的估计值。

设科氏流量计的一路信号为：

式中，A为信号幅度，f0为信号频率，θ1为信号初相。为不失一般性，f0可表示为如下形式：

式中，k0为整数；δ称为泄漏误差系数， ||δ≤0.5；fd称为频率分辨率，fd=fs/N；fs为采样频率，fs≥2f0；N为采样点数。以 fs同时对两路信号进行采样，得到采样序列：

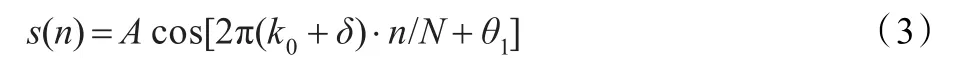
n=0，1，…，N-1，对 s(n)进行FFT变换，得到离散频谱S(k)，k=0，1，…，N-1，则 S(k)在 k=k0处具有最大谱线。由DFT的定义，得：

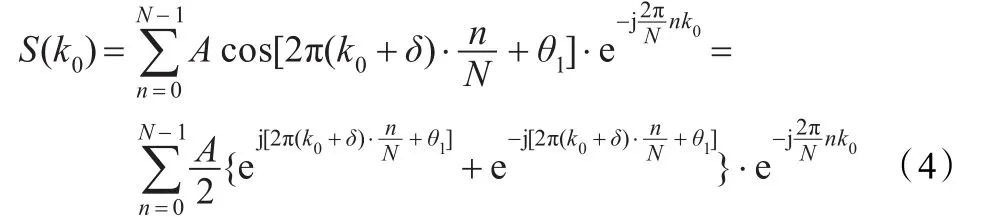
忽略负频率成分，只计算正频率部分，则有：

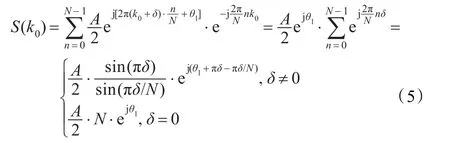
通过FFT计算出S(k)取得最大值的k0点，在不进行频谱修正的情况下，即认为δ=0时，得出：

设按等间隔对在0～T区间内进行采样，则式（5）可写为：

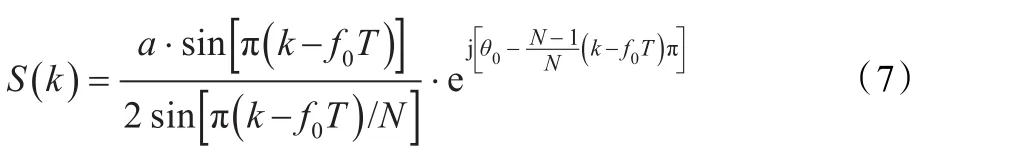
幅度最大值处的离散频率索引值记作k1,k1=int[ ] f0T, int[] x表示取最接近x的整数。对于较大的N，在幅值最大处，S() k的幅度可以近似表示为：

其中δ=( ) f0-k1Δf/Δf为信号频率与其DFT幅值最大处对应频率的相对偏差，Δf=1/T，δ的变化范围为－0.5～0.5。在紧邻k1的左侧和右侧的两条谱线中幅值较大处（以下称为幅度次大值，对应的离散频率索引值记作k2，k2=k1±1），S() k的幅度可近似表示为：

A2与A1的比值记作α，根据式（8）和式（9），有：

根据A2与A1的比值可以得到 ||δ的估计值[9]：

根据δ值可对由离散频谱得到的 f0的估计值进行插值从而得到更精细的频率估计值：

式中符号根据k2的位置确定，若k2=k1+1取加号，反之取减号。

2.2 计及负频率的滑动DTFT相位差估计

科氏流量计信号频率基本固定，流量的变化主要反映在信号相位差的变化上，所以要实现科氏流量计的高精度流量测量，相位差估计的精度和实时性是关键。DTFT法在计算相位差时忽略了频谱中负频率的影响[10-13]，导致相位差测量精度下降，同时，随着采样点数的增加，DTFT法计算量不断增大，导致算法效率低[7，14-15]。为此，本文提出采用计及负频率的滑动DTFT法计算科氏流量计信号相位差[15]，并且对该方法的循环迭代算法进行了改进以降低运算量和提高运算效率。

科氏流量计信号采样序列s1(n)和s2(n)可表示为如下形式：

式中，ω称为数字角频率或数字频率，ω=2πf0/fs。应用离散频谱校正方法求出ω的准确估计值，设为则s1(n)在处的DTFT为：

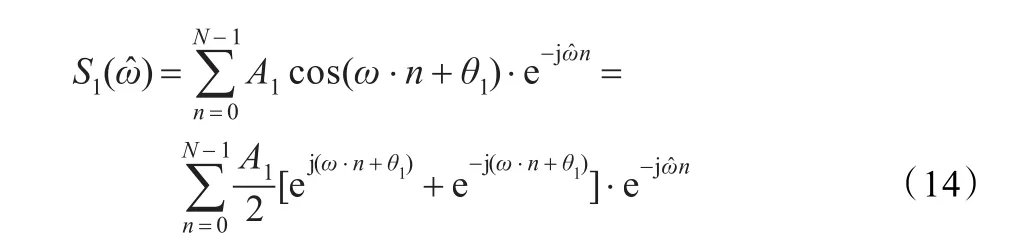
将负频率成分考虑在内，有：

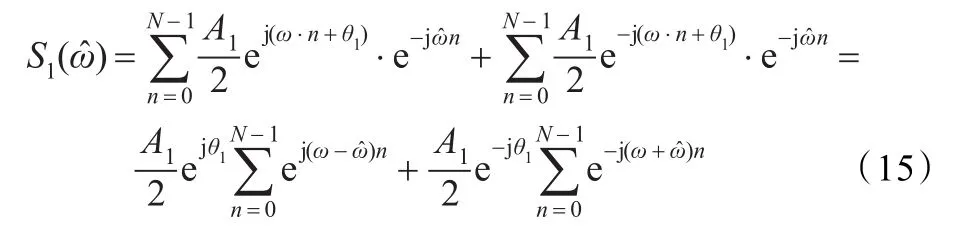
式中：

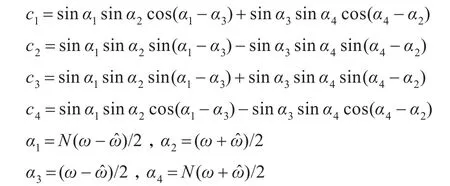
φ1为的相位。同理，对于第二路正弦采样序列s2(n)，有：

式中，φ2为s2(n)在处的DTFT（用表示）的相位，

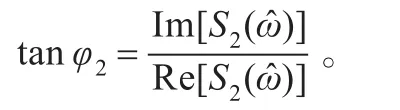
由式（16）和式（17）可求得两路信号之间的相位差：

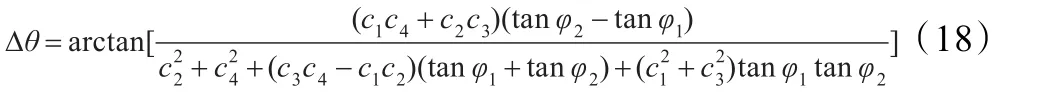
一般情况下，当信噪比不是特别低时，采用计及负频率影响的离散频谱校正方法求得的信号频率值与真实值很接近，即可以认为，sinα1/sinα3≈N，则式（18）可近似表达为如下形式：

式中：

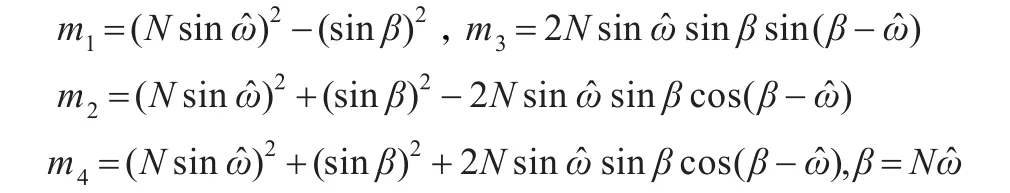
为避免计算量随采样点数的不断增加而增加，并避免冗余计算，本文对文献[15]进行了改进，采用滑动矩形窗来计算DTFT。设窗长为N点，x(n)为采样点，则第k号窗和k+1号窗的DTFT为：

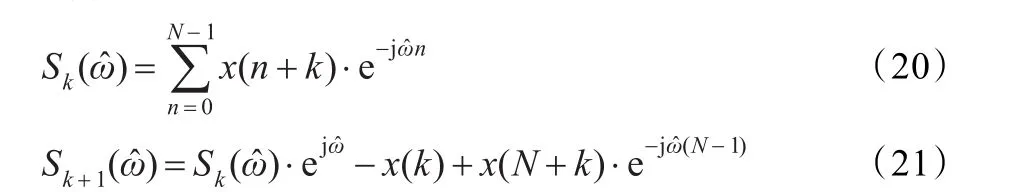
由式（21）知，每重新计算一次DTFT，只需要计算两次乘法及两次加法，大大减少了计算量，提高了计算效率，且计算的精度不受影响。

本文相位差估计方法归纳如下：

（2）分别计算s1(n)和s2(n)在处的DTFT，求出tanφ1和tanφ2。

（3）由ω和N求出m1～m4，并同tanφ1和tanφ2一起代入式（19）求出相位差。

（4）用式（21）循环迭代计算。

3 实验验证及分析

3.1 科氏流量计信号模型及实验

由于实测信号真实的频率以及相位差参数未知，为更好验证方法的有效性，本文采用改进的时变模型产生信号进行仿真实验，模型如式（22）：

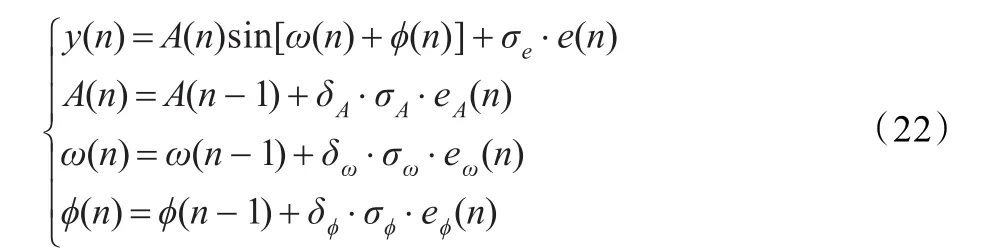
其中，e(n)、eA(n)、eω(n)和eφ(n)均为零均值、方差为1的白噪声，且彼此互不相关。参数σe、σA、σω和σφ决定对应参数的游动幅度，可视流量计的具体型号和应用环境而定，σA、σω和σφ的取值与采样频率 fs有关，在计算机仿真中，若 fs越大，则σA、σω和σφ需相应地取小些，反之亦然。δA、δω、δφ称之为游动因子，分别服从概率为PA、Pω、Pφ的0-1分布，决定信号幅度、频率、相位是否变化，P的大小依流量特性及应用环境而定。为使仿真信号接近实测信号，本文设定信号的初始频率值为198 Hz，初始相位差为0.002π，幅值、频率变化相对较小，信噪比高，相位差变化较大。图2给出了科氏流量计实测信号及仿真信号的结果，通过对比可知该信号模型能较好模拟科氏流量计实测信号。

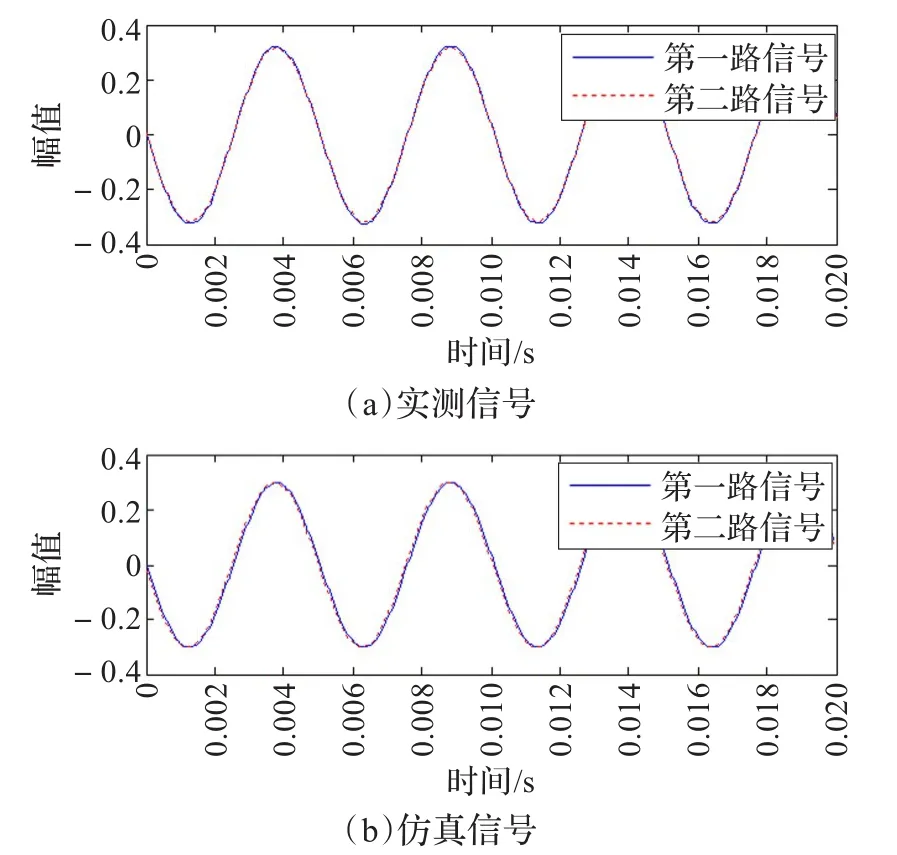
图2 科氏流量计实测信号及仿真信号

3.2 频率估计实验验证与分析

采用3.1节仿真信号进行频率估计的实验验证。图3为单次实验验证的对比结果，由图知FFT插值校正法相较于FFT法使频率估计的相对误差由9×10-4提高到2×10-5。为进一步验证本文方法的普适性，分别对FFT法和FFT插值校正法进行频率估计蒙特卡洛随机实验500次，再计算频率估计的均方误差，结果FFT法频率估计均方误差为5.82×10-3，FFT插值校正法为4.37×10-4。实验结果表明，本文采用的FFT插值校正法大幅度提高了FFT法频率估计的精度，与文献[7]所采用的自适应陷波器方法相比，在精度不降低的前提下，减少了计算量，大幅度提高了计算效率，且稳定性更好，不存在自适应陷波器的非稳定跟踪问题。

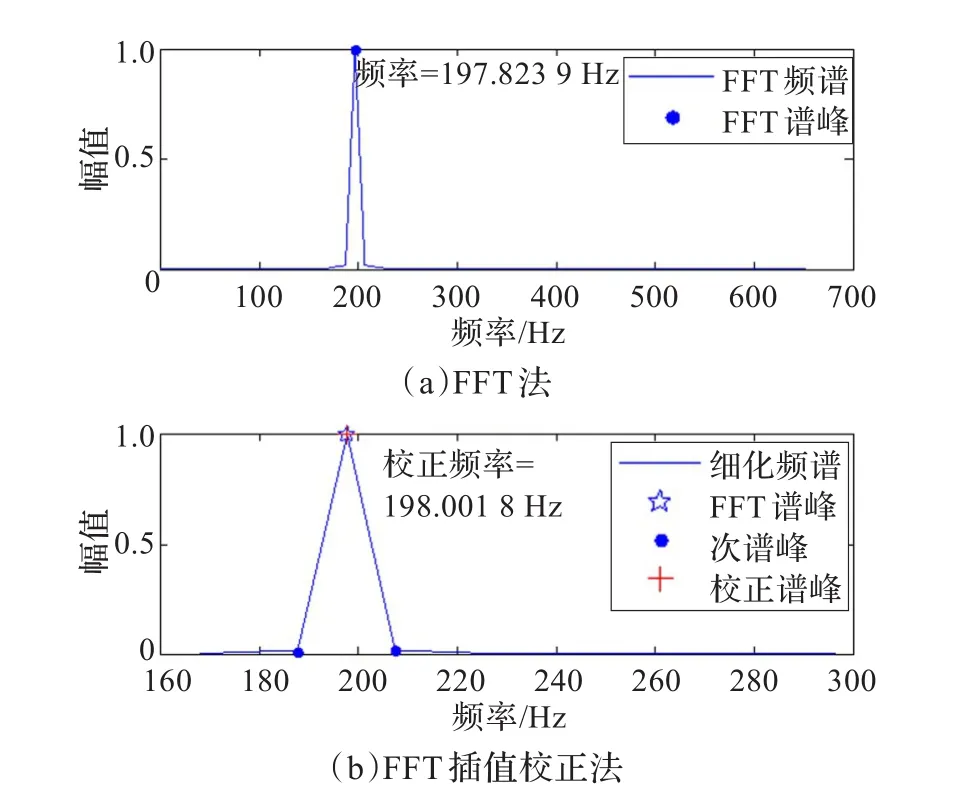
图3 差值FFT估计频率

3.3 相位差估计实验验证与分析

采用3.1节仿真信号进行相位差估计实验的结果如图4、图5所示。

图4给出了信号真实相位差、DTFT法估计的相位差、本文方法估计的相位差对比结果，表明本文方法能很好跟踪信号相位差的变化，且跟踪效果明显优于DTFT法。图5为综合运用本文的频率估计法及相位差估计法计算的科氏流量计两路信号时间差结果，表明本文所提方法在跟踪精度和跟踪的实时性上明显优于DTFT法，能够精确计算科氏流量计信号频率，实时跟踪两路信号之间相位差的变化，其计算的时间差与相位差的变化趋势一致，进一步验证了本文方法的有效性及优越性。

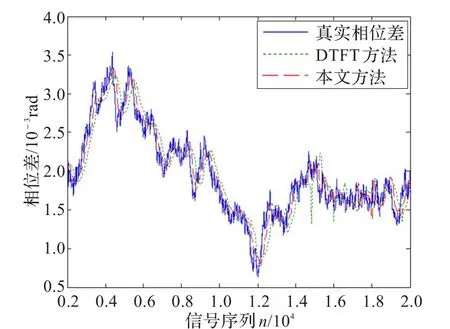
图4 相位差估计比较

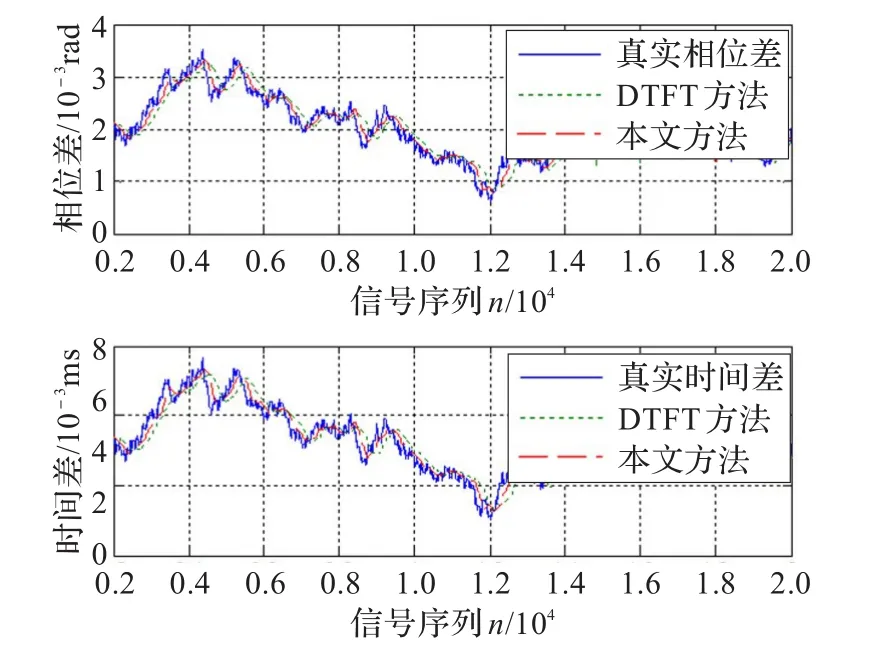
图5 时间差估计比较

表1为在不同相位变换幅度和不同初始相位差条件下DTFT法和本文方法进行蒙特卡洛随机实验500次的对比结果。结果表明，与DTFT法相比，本文方法计算的相位差和时间差均方误差值均较小，当相位变化幅度较小时，DTFT法的精度下降明显，而本文方法精度基本无变化，具有较高精度，验证了本文方法的有效性和稳定性。

4 结束语

本文针对科氏流量计实测信号提出了一种科氏流量计数字信号处理方法：用FFT插值校正法估计信号频率，用改进的滑动DTFT法估计相位差，进而求得时间差。实验结果表明，本文方法频率估计的精度相较于FFT法有了大幅度提高，相较于自适应陷波器法，保持了估计精度、减少了运算量、提高了稳定性；相位差估计的精度和稳定性均优于DTFT法，改进的循环迭代算法降低了运算量，能够实时跟踪信号相位差变化，精度较高；通过本文方法计算出的时间差能够反映信号时间差的真实变化情况，验证了本文方法的有效性及优越性。

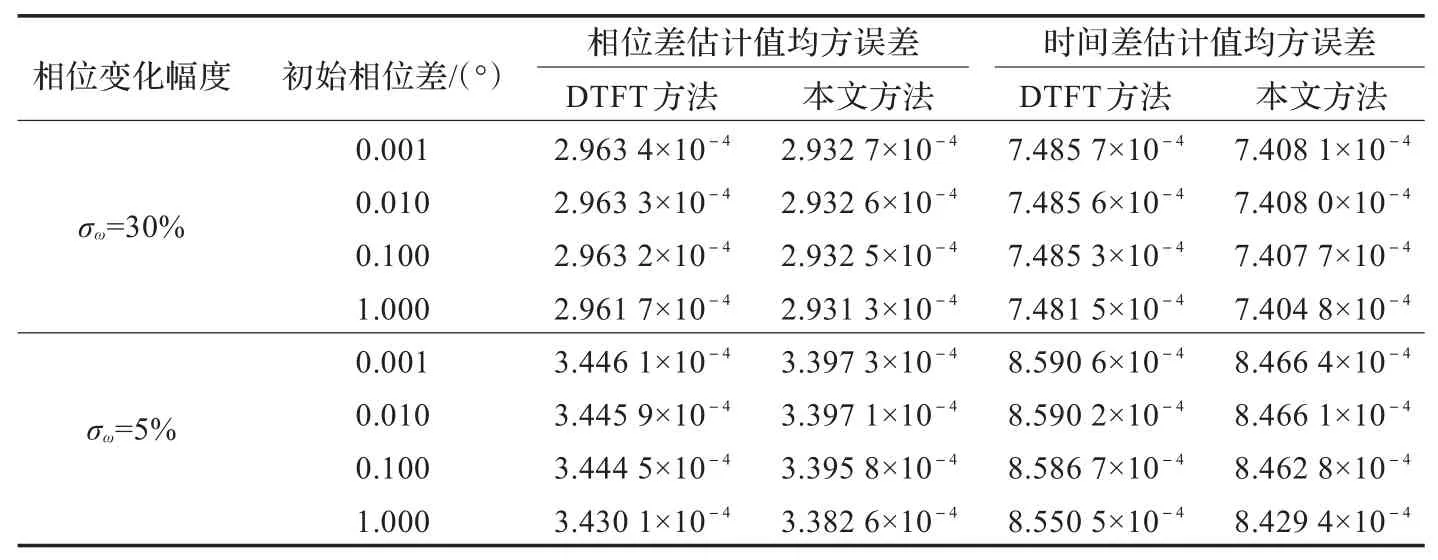
表1 相位差和时间差估计均方误差值的比较

[1]Cheesewright R，Clark C.The effect of flow pulsations on Coriolis mass flow meters[J].Journal of Fluids and Structures，1998，12：1025-1039.

[2]Cheesewright R，Clark C，Bisset D.The identification of external factors which influence the calibration of Coriolis massflow meters[J].Flow Measurement and Instrumentation，2000，11：1-10.

[3]李叶，徐科军，朱志海，等.面向时变的科里奥利质质量流量计信号的处理方法研究与实现[J].仪器仪表学报，2010，31（1）：8-14.

[4]杨辉跃，涂亚庆，张海涛.基于Hilbert变换的相位差测量方法分析及改进[J].四川兵工学报，2011，32（1）：107-109.

[5]苏奋华，涂亚庆，张海涛.科里奥利质量流量计信号频率跟踪方法研究现状与展望[C]//中国智能自动化会议.南京：[s.n.]， 2009：993-998.

[6]涂亚庆，苏奋华，沈廷鳌，等.新式自适应陷波器的科氏流量计信号频率跟踪方法与仿真[J].重庆大学学报，2011，34（10）：147-152.

[7]沈廷鳌.科氏流量计信号频率跟踪方法及相位差算法研究[D].重庆：后勤工程学院，2011.

[8]Ban S J，Lee C W，Cho H.A variable step-size adaptive algorithm for direct frequency estimation[J].Signal Processing，2010，90：2800-2805.

[9]齐国清，贾欣乐.插值FFT估计正弦信号频率的精度分析[J].电子学报，2004，4（4）.

[10]胡广书.数字信号处理—理论、算法与实现[M].2版.北京：清华大学出版社，2003.

[11]Yoshimura H.Phase difference measuring apparatus and flowmeter thereof：European，EP 0702212A2[P].1996-04-14.

[12]刘凤新，简灿琴.基于窄带滤波及分组DTFT的科氏流量计信号处理方法[J].计量技术，2009（4）：17-21.

[13]刘凤新，朱家雄.一种新颖的科氏流量计数字信号处理方法[J].计量学报，2010（2）：127-130.

[14]张海涛，涂亚庆.基于DTFT的一种低频振动信号相位差测量新方法[J].振动工程学报，2007，20（2）：180-184.

[15]张海涛，涂亚庆.计及负频率影响的科里奥利质量流量计信号处理方法[J].仪器仪表学报，2007，3（3）：539-544.

YI Peng,TU Yaqing,YANG Huiyue

Department of Information Engineering,Logistical Engineering University,Chongqing 410311,China

Coriolis flowmeter measures mass flow by computing the time difference of two sinusoidal signals outputted with the same frequency by its primary instrument.It is crucial to estimate the frequency and phase difference of the two signals accurately and real-time in the digital signal processing of Coriolis flowmeter.Using the actual Coriolis flowmeter signals collected,it presents a method to calculate time difference which based on interpolation FFT for frequency estimation and through improved sliding DTFT considering negative frequency for phase difference estimation.This method balances high precision with computational efficiency.Contrast experiment verifies the availability and advantage of this method.

Coriolis mass flowmeter;digital signal processing;interpolation Fast Fourier Transform（FFT）;sliding Discrete Time Fourier Transform（DTFT）;phase difference

科氏流量计通过计算一次仪表输出的两路同频正弦信号的时间差来测量质量流量。实时精确估计两路信号的频率和相位差是科氏流量计数字信号处理的关键。针对科氏流量计实测信号，提出一种基于插值FFT和滑动DTFT的信号处理方法。利用插值FFT估计信号频率，通过计及负频率的改进滑动DTFT估计相位差，进而计算出时间差。方法兼顾了参数的估计精度和算法的计算效率，对比实验表明了该方法的有效性和优越性。

科氏流量计；数字信号处理；插值快速傅里叶变换（FFT）；滑动离散时间傅里叶变换（DTFT）；相位差

A

TH814

10.3778/j.issn.1002-8331.1207-0236

YI Peng,TU Yaqing,YANG Huiyue.Signal processing method of Coriolis mass flowmeter based on interpolation FFT and sliding DTFT.Computer Engineering and Applications,2013,49（5）：236-240.

国家自然科学基金（No.60871098，No.61271449）；重庆市自然科学基金（No.CSTC2011BA2015）。

易鹏（1988—），男，硕士生，研究方向：智能测控理论与技术；涂亚庆（1963—），男，博士，教授，博导，研究方向：智能测控理论与技术；杨辉跃（1987—），男，博士生，研究方向：智能测控理论与技术。

2012-07-17

2012-09-28

1002-8331（2013）05-0236-05

CNKI出版日期：2012-10-23 http://www.cnki.net/kcms/detail/11.2127.TP.20121023.1539.003.html

◎工程与应用◎