基于矢量阵列的信源数估计算法

李 楠 程锦房 何光进 张 炜

（海军工程大学兵器系 武汉 430033）

空间信号的波达方位估计是空间谱估计中的重要研究方向，其中大部分算法均需要知道入射信号源数，但在实际场合情况下信号源数往往未知，这就需要预先估计信号源数.如果信源数估计错误，就会导致信号子空间和噪声子空间划分不准，即两者不能完全正交，从而造成估计信号源时的漏报或虚警，同时导致信号波达方位的估计偏差.因此，只有准确估计出信号源数才能有效地获取信号源的波达方位.

目前常用的信号源数估计方法有：基于信息论准则的方法、盖氏圆方法、平滑秩法、矩阵分解法以及正则相关等方法［1－2］.基于信息论的 AIC准则不是一致性估计，即在大快拍数的场合，仍然有较大的误差概率，而最小描述长度准则是一致性估计，也就是在高信噪比情况下该准则有较好的性能，但在小信噪比条件下该准则相比AIC有高的误差概率.盖氏圆方法需要人工设置阈值，且在信噪比较低时常常会产生欠估计或过估计.平滑秩法和矩阵分解法只适用于高信噪比和大快拍条件，且两者均是以牺牲阵列孔径为代价的.正则相关技术需要2个空间分离的阵列，硬件开销大，实际应用中有困难.

文中提出一种基于核一致判别的信源数估计方法，它利用并行因子分析方法表示信号协方差张量，通过计算该模型的秩来确定信源数，由于矢量水听器声压和振速通道均含有信源数信息，本方法能够充分利用多路信号的特点，在低信噪比和小快拍条件下实现信源数的估计.本文将它称之为核一致判别信源数估计方法.

1 矢量阵列输出互谱张量模型

一均匀线阵由M个矢量水听器组成，用来接收R个远场窄带信号，单矢量水听器信道数为Nc.设各个信号源发出的信号对于该均匀线列阵的入射角为（θ1，θ2，…，θR），则矢量阵的输出模型为

式中：A（φ）＝ ［a（φ1）⊗u1，a（φ2）⊗u2，…，a（φR）⊗uR］；符号 ⊗ 表示Kronecker积，又称直积；a（φr）＝ ［1，e－jβr，…，e－j（M－1）βr］T为信号导向矢量为相邻阵元间同一信号的相位延迟；ur＝ ［1，cosθr，sinθr］为信号传播矢量；S（t）＝［xi1（t），xi2（t），…，xiM（t）］T为入射信号波前矩阵（i＝1，2，…，Nc）；N（t）为噪声矩阵.设信号和噪声不相关，各阵元接收到的信号互相独立，则输出信号协方差为一个4阶张量（M×Nc×M×Nc.其中：M为阵元数；Nc为单矢量水听器信道数）.

2 并行因子分析

并行因子分析最早应用在化学光谱分析中，仅仅是在近几年才被引入到阵列信号处理当中来.它是一种多维低秩分解方法，是二维低秩分解的扩展.以三维张量X∈CI×J×K为例，它可以分解为

式中：ar，br，cr分别为矩阵A∈I×R，B∈J×R和C∈K×R的第r列向量；N∈CI×J×K表示噪声，见图1.实际情况下，信源功率一般是不等的，为提高信源数的估计性能，要对信号的功率进行归一化，使得

图1 三阶张量并行因子分解

任意一个三阶张量X秩的定义与矩阵秩的定义类似，即分解张量X所需要的秩为1的三阶张量的最小数目［3］.并行因子分析方法的最大优点是它的分解具有惟一性，而在传统的矩阵双线性分解中，如果没有足够的辅助信息（例如统计独立、正交等条件）一般分解不惟一，另外并行因子分析对噪声也具有较强的鲁棒性.下面通过核一致判别法确定张量的秩，从而实现信源数的估计.

3 核一致判别法估计信源数

为便于讨论和读者理解，这里仍以三阶张量［4］为例进行说明，该方法可以直接向更高阶扩展（本文输出信号协方差为四阶张量）.

考虑一个三阶秩R并行因子分析模型的矩阵化形式，它可表示为

式中：X∈CI×JK为张量X∈CI×J×K的矩阵化形式，即表示张量X的切片展开；矩阵A∈CI×R，B∈CJ×R，C∈CK×R和N∈CI×JK.⊙表示 Khatri－Rao积.

文献［4］表明，并行因子分析模型是Tucker3模型的一种特殊形式，所以经过信源功率归一化后，上面并行因子分析模型又可写成如下形式

式中：核矩阵T（R×RR）为张量T∈CR×R×R的切片展开形式，张量T是三阶超对角张量，即张量元素满足

式中：δ（·）为Kronecker函数.

矩阵A∈CI×R，B∈CJ×R，C∈CK×R均含有并行因子分析模型的秩信息，即信源个数信息，为有效提取三阶张量秩，需计算下式的极小值［5］

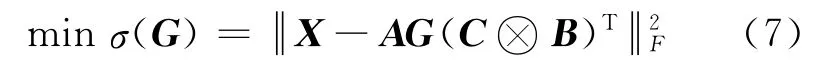
式中：矩阵G∈CR×RR是三阶张量G∈CR×R×R的切片展开形式.

由文献［6］可知式（7）可写成如下形式

式中：vecX为矩阵X的向量化表示.

式（12）的极小值解为

式中：＋为矩阵（C⊗B⊗A）的广义逆.

经研究发现［7］，噪声能量在张量核G∈CR×R×R中的分布具有趋于均匀化的特性，即张量G∈CR×R×R中的每个元素具有相近似的值，而信源能量在张量核G∈CR×R×R中的分布主要集中于超对角线上，尤其信源在功率归一化后，张量核G∈CR×R×R与超对角张量T∈CR×R×R的差范数为零，即.通过计算核张量G与T的相似性最终确定信源数，这就是本文的理论基础.

核一致性可表示为

对于秩为1的张量核，由于没有非对角元素，所以核一致性为100%，随着张量秩R的增加，核一致性会减小，当秩R达到最大（即达到该张量秩真值）时，若再增加秩R，则核一致性会迅速降低，原因在于噪声的引入会导致非超对角线元素值的迅速增长，这就是判别张量秩的主要依据.

以上讨论都是基于信源之间是相互独立情况下进行的，但实际上存在信源间存在相关甚至相干的情况，所以与二阶矩阵类似，在确定张量秩之前需对信号谱张量进行空间平滑，方法采用与文献［8］相同的方法即可.

4 算 例

为研究文中提出的核一致判别确定信源数方法的性能，进行了大量的数值计算，结果如下.

算例1研究核一致判别信源数估计的成功概率随信噪比的变化，并与盖氏圆法和最小长度描述法进行比较.设有10个阵元矢量水听器线阵，阵元间距为半波长，3个独立的窄带信号分别以15°，45°和60°的入射角入射到均匀线阵上，信号频率为100Hz，噪声为空间高斯白噪声，快拍数为50，信噪比由－5dB变到20dB.核一致判别法、盖氏圆法和最小长度描述法分别独立估计信源数300次，用蒙特卡洛法得到各自的正确估计概率，见图2.由图2可见：在低信噪比时，核一致判别法估计成功概率明显好于盖氏圆和最小描述长度法，此外，盖氏圆法需要根据经验进行人工设定判据的阈值.

图2 3种方法估计正确概率随信噪比的变化

图3 3种方法估计正确概率随快拍数的变化

算例2研究在不同快拍条件下，核一致判别法估计信源数成功的概率，并与盖氏圆法、最小描述长度法进行比较.设有2个独立的窄带远场信号入射到均匀线阵上，入射角度分别为30°和75°，快拍数由30变化到180，信噪比为5dB，其他条件同算例1，用蒙特卡洛法计算，结果见图3.由图3可见：在小快拍条件下，核一致判别法依然要好于盖氏圆法和最小描述长度法，原因在于矢量水听器具有多路信号接收优势，能弥补采样数目小的缺点.

算例3研究独立信源入射角夹角与信源数估计正确概率的关系，设信噪比为5dB，快拍数为100，2个独立窄带信号入射到均匀线列阵上，一个信号入射角为40°，另一个信号的入射角由41°变到50°，间距为1°，用蒙特卡洛法估计200次，其他条件同算例2，结果见图4.由图4可见，核一致判别法明与盖氏圆法估计概率基本相当，优于最小描述长度法，在夹角大于5°后，本文提出的方法估计的准确概率近似为1.

图4 3种方法估计正确概率随夹角变化

算例4研究空间相关色噪声下信源数估计正确概率，并与盖氏圆法、最小描述长度法进行比较，空间相关色噪声采用文献［9］提供的模型，其他条件同算例2，信噪比为10dB，结果见图5.由图5可见：在相关系数大时，本文提供的方法明显好于盖氏圆法和最小描述长度法.

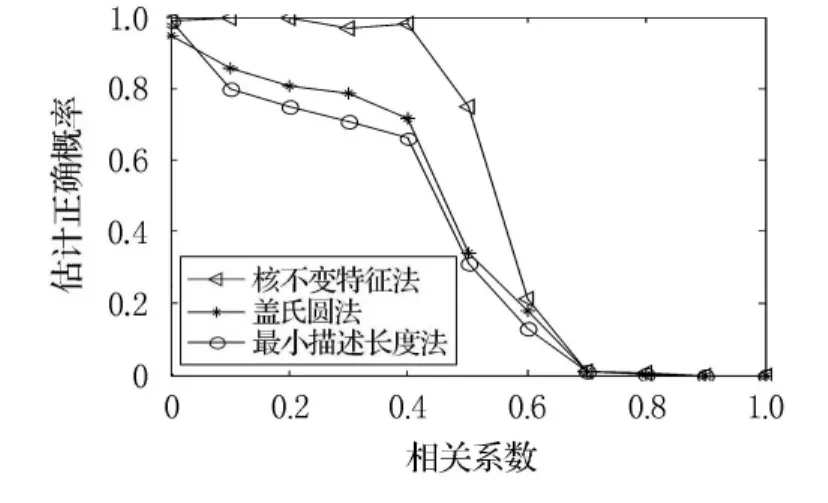
图5 空间相关色噪声下3种方法估计正确概率比较

5 结束语

信源数准确估计是很多方位估计的重要前提和基础，以往基于矢量水听器的方位估计算法都是利用声能流对各向同性噪声的良好抑制实现的，但就如何提高声矢量阵在信源数的估计准确度方面没有提出切实可行的办法.本文通过多维信号处理提取了振速通道内含有的信源数信息，比传统方法能够在更恶劣的环境噪声情况下得到信源数，从而为后续方位估计提供基础.

［1］WAX M，KAILATH T.Detection of signals by information theoretic criteria［J］.IEEE Trans.On ASSP，1985，33：387－392.

［2］周 天，李海森，么 彬.近场源定位算法在水声主动成像系统中的应用［J］.武汉理工大学学报：交通科学与工程版，2008，30（5）：135－138.

［3］ACAR E，YENER B.Unsupervised multi－way data analysis：a literature survey［J］.Transactions on Knowledge and Data Engineering，2009，21（1）：6－18.

［4］龚晓峰，刘志文，徐友根.电磁矢量传感器阵列信号波达方向估计：双模 MUSIC［J］.电子学报，2008，36（9）：1698－1073.

［5］MIWAKEICHI F，MARTINEZ M E，VALDES S P，et al.Decomposing EEG data into space－time－frequency components using parallel factor analysis［J］.NeuroImage，2004，22（3）：1035－1045.

［6］张贤达.矩阵分析与应用［M］.北京：清华大学出版社，2006.

［7］ESTIENNE F，MATTHIJS N，MASSART D，et al.Multi－way modelling of high－dimensionality electroencephalographic data［J］.Chemometrics and Intelligent Laboratory Systems，2007，58（1）：143－152.

［8］THAKRE A，HAARDT M，GIRIDHAR K.Single snapshot R－D unitary tensor－esprit using an augmentation of the tensor order［C］／／3rd IEEE International Workshop on Computational Advances in Multi－Sensor Adaptive Processing，2009：303－310.

［9］张 杰，廖桂生，王 珏.空间相关色噪声下基于变换的信源数目标估计［J］.电子学报，2005，33（9）：1581－1585.