基于双层规划的道路客运班线运力优化研究

黄 涛 潘 青 徐 亚

（武汉理工大学交通学院 武汉 430063）

道路旅客运输由于其灵活方便性，成为旅客出行的主要运输方式之一，道路班线客运运力与运量的平衡，是道路班线运输系统优化的目标.由于社会经济的发展，客运需求也是稳定增长，如果投入客运运力不足，就不能满足旅客的正常出行需求，同时也会影响到社会经济的发展，相对如果客运运力过量，也会造成社会资源的浪费，同时还会导致道路客运行业的内部竞争消耗.随着国民经济持续快速增长和人民生活水平不断稳步提高，居民出行对客运服务水平的要求也不断提高，道路旅客运输需要提供不同层次的服务以满足旅客不同层次的需求，最大化客运企业及旅客利益以保证道路客运在竞争激烈的客运市场稳定发展，合理优化道路班线运力以提供不同层次的服务来满足旅客需求就显得十分必要.总之合理的班线客运运力对于道路客运发展有着十分重要的意义，为此本文将采用双层规划的方法研究班线运力的优化问题，为客运企业确定合理的运力以满足旅客出行需求及企业最大化利益提供参考.

1 双层规划基本原理

双层规划模型的结构形式分为上下2个层次，上下层次都有其各自不同的目标函数，同时本层的决策空间受其他层次的影响.相比传统单层规划模型，决策者同时控制的决策变量不同，双层规划模型中各层的决策者仅控制本层的决策变量［1］.双层规划模型的数学表达式为

上层模型（U）

式中：y＝y（x）通过下层模型求解得到.

下层模型（L）

上层决策者可以通过决策变量来影响下层决策者，同时也会与下层决策者发生相互作用；下层模型的决策变量y是上层模型决策变量x的函数，即y＝y（x），通常相对于上层模型这个函数被称为反应函数，而相对于下层模型则被称为反应模型.

将道路客运班线运力规划问题看作一个双层规划问题.运量供给要求有运量需求来实现，而运量需求又要求有运量供给来满足.运量供给的能力制约着需求的增长又必须适应需求，运量需求的满足取决于供给的数量和质量，并且运量需求的变化又会引起供给的变化.营运班线的建立，必须综合考虑客运企业与旅客的利益.道路客运企业决定班线运力的投入以及不同的运力结构，而旅客则根据自身的条件选择出行行为［2］.充分考虑运输企业和旅客两方面的利益，利用双层规划模型来优化班线配置运力.

上层规划问题可以表示为道路客运企业根据客运需求投入运力及决定运力组成，并在规定范围内制定不同车型的票价，要求合理的运力及运力组成使道路客运企业取得最大的经济效益的同时满足旅客的出行需求.

而下层规划问题则描述了多种运输方式竞争条件下，旅客依据不同的状况选择不同的运输方式，也就是客流量在不同客运方式（车型）之间的分配，下层模型中旅客的选择行为可以利用满意度来刻画，在确定的运力下使旅客总体的满意度最大.

2 班线运力优化双层规划模型

基于上述建模思想，建立道路班线运力优化双层规划模型，上层优化问题由客运企业决策投入运力，下层优化问题由旅客决策选择运输方式（车型），双层规划的目标就是确定合理的班线运力使旅客总体满意度最大与客运企业利润最大达到平衡［3］.

2.1 上层优化问题

在建立上层模型时，首先设定道路客运班车分为豪华快车、普通快车与普通车，不同车型票价不同，不同车型的组合以满足旅客不同层次的出行需求，使旅客出行总体满意程度最高，同时也使得运输企业获得最大利润［4］.假设某班线豪华快车、普通快车与普通车的运力分别为xi，i＝1，2，3.

首先班线运力要能满足旅客的基本出行需求的要求，用Q表示班线旅客出行需求，班线客运需求Q可以通过各种适合的定性定量预测方法得到，具体约束表达式为［5］

式中：s为平均实载率；r为工作车率；l为车日行程；L为该班线的运输距离.

客运企业的收益为

式中：qi为班线中选择客运方式i的客流量；pi为票价；ci为客运变动成本，在其他条件不变的情况下，运力xi投入越大，发车时间间隔越小，服务水平越高，则客流量qi越大，为此qi可以表示为xi的函数q（xi），而q（xi）则由下层规划模型确定.

上层模型（U）

式中：g（xi）为客运企业投入运力xi的成本；θ为折旧系数.票价约束中pl，pu为政府管理部门规定的票价下限与上限.在实际中，票价是不易改变的的变量，因此可以选择现行票价作为常系数，当然如果新开通班线时，这里可以将票价取做变量，通过模型求解确定合理的初始参考票价.

2.2 下层优化问题

下层优化模型在效用理论的基础上，提出旅客出行选择行为模型，也就是在假定其他条件不变的情况下，当道路客运企业投入不同运力的时，旅客总是选择满意度最大运输方式出行，而下层模型就是以旅客总体满意度最大为目标.

首先需要建立合理的旅客出行满意度函数，而影响旅客出行满意度的因素有很多，在这里假定其他影响因素都是固定的，仅仅考虑不同方式运力投入以及票价对旅客出行选择行为的影响，构建不同运力投入及票价下旅客满意度函数.根据经济学知道，人的满足感存在边际效用，也就是当服务水平较低时，服务水平一定程度的提高就能引起旅客满足感的大幅提高，随着服务水平的不断提高旅客满足感的提高程度会越来越小，为此本文采用的满意度函数为

式中：αi为常系数，用来调整不同运力及票价对旅客满意程度影响程度的大小，系数βi的标定需要依据人们的心理因素及价值标准；系数αi用来调整旅客的拥挤对满意度的影响程度的大小，其标定也取决于旅客的心理因素.系数αi，βi可以利用经验定性的确定，也可以通过调查采用统计学方法确定.

下层模型（L）

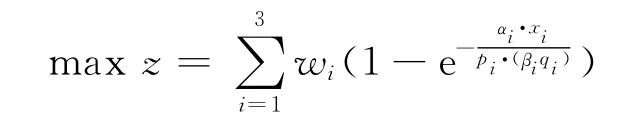
式中：系数wi为不同客运方式旅客满意度对总体满意度贡献的权重，这里wi可以取不同客运方式的客流量占总的旅客客流量的比例：wi＝不同客运方式的客流量qi为下层模型的决策变量，不同方式客流量的加和满足与此班线上旅客总的出行需求量相等.下层规划中不同方式客流量qi是为了在不同的运力xi及票价pi下使旅客总体满意度最大.

双层规划方法比传统的单层规划方法相比具有很大优势.（1）可以同时分析决策过程中2个不同的相互矛盾的目标；（2）更接近所研究问题的实际情况；（3）可以明确表示客运企业与旅客的相互关系.模型的求解可以采用数值优化算法，也可以采用遗传算法等，此处不做过多介绍.下面介绍一种模型的启发式算法.

3 模型的启发式算法

求解上述班线运力优化双层规划问题的关键在于寻找反应函数q（xi）的具体表达形式，但是q（xi）的表达式是很难准确的得到的，为此可以通过灵敏度分析方法得出道路班线某种客运方式的客流量对其运力的导数关系，这样就可以利用泰勒展开式对反应函数进行线性的近似，从而简化反应函数以求解双层规划问题，这就是基于灵敏度分析方法的启发式算法［6］.假设班线运力的初始值为，i＝1，2，3，票价为企业依据市场情况制定，在模型中视为常数，通过下层模型便可以求解出在此运力水平下，各种运输方式的均衡客流量），通过灵敏度分析法得到各种客运方式的客流量对其运力的导数关系为∂qi／∂xi.于是可以得到qi（xi）函数的泰勒展开式的近似形式为

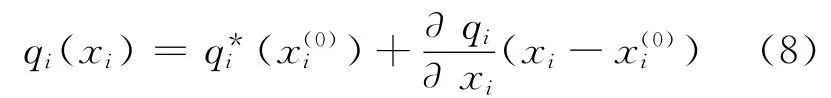
将式（8）代入到上层规划模型中，则可以求解上层模型，得到新的平衡客流量下的各种客运方式的运力最优组合，将此结果再次代入下层模型重复上述过程，直到解收敛于双层模型的最优解［7］.

具体的计算步骤如下.

步骤1设定初始的班线运力，i＝1，2，3，此时迭代次数k＝0.

步骤2在班线运力的条件下，求解下层规划模型，得到班线上各种运输方式平衡客流量（）.

步骤3采用灵敏度分析法计算班线客流量对各运输方式运力的导数，利用泰勒展开计算得到上层模型反应函数（xi）.

步骤4将（xi）代入到上层规划模型中，求解上层模型，计算得到当前状态下最优的班线运力组合xi（k＋1），i＝1，2，3.

步骤5判断收敛条件，若ε，∀i＝1，2，3，则停止计算，否则，k＝k＋1，并转入步骤2，其中ε代表规定的迭代精度.

4 算 例

以武汉地区道路客运中武汉至黄石班线为例，运用班线运力双层规划模型优化武汉至黄石班线的运力，此处算例仅仅是为了展示模型的可行性，为此算例中的参数都是在定性分析基础上设定的，实际应用中可以依据统计分析的方法获得并校正这些参数，使模型计算结果更为科学合理.武汉到黄石距离115km，道路客运运力方式有：豪华快车、普通快车以及普通车.预测道武汉市黄石路客运需求量为1 770人次／d.那么道路客运运力约束可以表示为以日客运能力应该能满足日旅客出行需求，具体表达式为

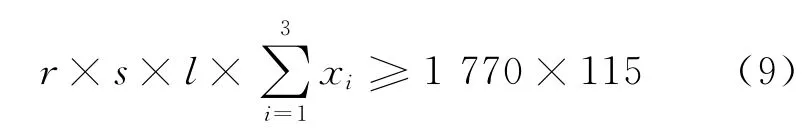
式中：平均实载率s＝0.8；工作车率r＝0.9；车日行程l＝400km／d.

本例中不同车辆的票价pi由客运公司依据市场情况制定，取固定值，不同车型具体情况见表1.

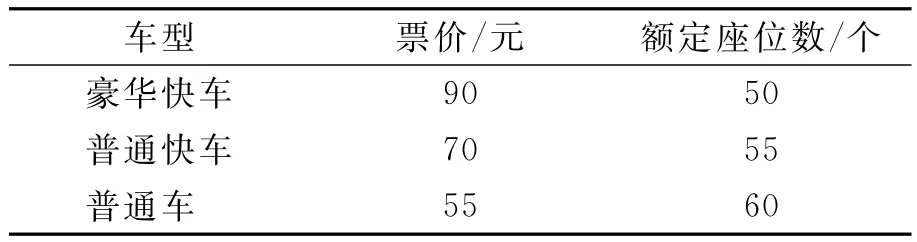
表1 道路客运车型基本情况

运力xi，i＝1，2，3表示豪华快车、普通快车与普通车总的座位数，以此除以各车的额定座位数便可以计算得到各车型的车辆数.

上层规划中的其他参数取值见表2.其中单位运力投入成本表示的为每台车辆的投入成本，日折旧系数是将资产成本投入均摊到每个工作车日，采用直线折旧法，折旧期限为10年，净残值为零.

下层规划模型参数取值见表3.

表2 上层模型参数

表3 下层模型参数

其中系数αi，βi的标定取决于旅客的出行心理及出行选择行为，选择普通车的旅客更多考虑的是优惠的票价，而选择豪华快车的旅客更看重车内舒适程度.此处在定性分析的基础上确定了αi，βi的取值，见表3.实际应用中可以结合经验及统计数据对系数进行校正，已达到满意的效果.

最后可以得到武汉至黄石班线运力优化双层规划模型为

上层模型（U）

下层模型（L）

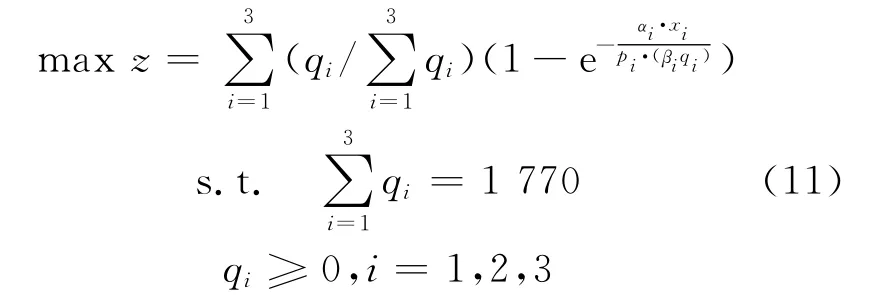
利用前面介绍的基于灵敏度分析方法的启发式算法求解得到结果：武汉至黄石班线最优总运力为车辆13台共690座，其中豪华快车7辆，普通快车4辆，普通车2辆，班线上豪华快车、普通快车及普通车的均衡客流量分别为849，533，291人次／d.

5 结束语

道路客运作为重要的旅客运输方式之一，对国民经济的发展有着重要的作用.合理的优化班线运力对道路客运班线发展有着重要意义，现有的班线配置方面的研究主要集中在班线配站方面，对于具体班线运力优化的研究较少.本文针对班线运力的优化展开研究，以道路客运企业盈利最大化为目标，建立上层班线运力决策模型；以效益理论为基础，构造了旅客满意度函数，建立下层客流分配决策模型.依据模型的特点给出了基于灵敏度分析方法的启发式算法，并以武汉至黄石班线为例验证模型的可行性与科学性.但在模型求解过程中假设票价依据市场而定为已知常数，同时模型中系数的确定也多为定性分析，而合理的标定这些系数影响着模型的应用价值，为此在票价作为变量时模型的求解及模型系数的标定方面可以做进一步的研究.

［1］宋一凡，高自友.连续平衡网络设计问题的双层规划模型及其求解算法［J］.公路交通科技，1999（1）：40－43.

［2］陆化普.交通规划理论与方法［M］.北京：清华大学出版社，1998.

［3］王 炼.线路客运运力需求预测及运力调控模型［J］.西安公路交通大学学报，1998，18（1）：113－116.

［4］靳文舟，张 杰.公路客运站运力配置方案优化研究［J］.华南理工大学学报：自然科学版，2000，28（6）：123－128.

［5］李维斌，邵振一.公路运输组织学［M］.北京：人民交通出版社，1998.

［6］PARK M，SMITH R L.Development of a statewide truck－tracel demend model with limited origin－destination survey date［J］.Transportation Reseaerh Reeodr，1997，1602：14－21.

［7］GAO Z Y，SI B F.An equilibrium assignment model for mixed network［C］／／Proceedings of ICTTS′98，1998：129－135.