一个混沌系统保密通信电路的构造

杨留猛，俞建宁，安新磊，张文娟，张建刚

(兰州交通大学 数理与软件工程学院，兰州 730070)

自1997 年以来，混沌保密通信成为了保密领域研究的热点，他因信息量大，保密方式奇特、新颖、易变和复杂而受到人们的重视。文献［1 -2］根据Lorenz 系统、Chen 系统、Lü 系统的混沌特性实现了自结构同步下的信息掩盖;文献［3 -5］分别从异结构混沌系统、多级混沌系统、复杂网络等角度提出了各自的保密方案。最近几年，基于混沌和混沌同步的保密通信一直是研究的热点［6-7］，然而，通过物理方法实现信息的有效掩盖却是1 个难题。

本文首先引入1 个具有复杂混沌吸引子的非线性混沌自治三维系统模型，并对其对称性、耗散性进行了分析。通过数值仿真和电路仿真证实了吸引子的存在性。最后，基于线性反馈同步控制理论设计了系统的保密通信电路。

1 混沌模型

1.1 模型引入

首先根据文献［8］引入1 个混沌系统

其中:x，y，z∈R 为状态变量;a，b，c，h 为已知常数。当a=35，b =3，c =28，h =20 时，系统(1)存在1 个混沌吸引子，其相轨迹如图1 所示。

图1 系统(1)的1 个混沌吸引子的数值仿真

1.2 对称性和耗散性

系统(1)在变换P:(x，y，z)→(-x，-y，z)下对所有的参数a，b，c，h 都具有不变性。所以，系统(1)关于z 轴对称。

由于系统(1)的向量场散度

所以当-(a+b-c)＜0 时，系统(1)是耗散的，并且以指数形式收敛。由此可知，系统的所有轨线最终会被限制在1 个体积为0 的点集合上，这就说明了吸引子的存在性。当系统满足a+b-c ＞0 时，系统的非线性电路能够实现。

2 电路实验

根据非线性电路构造原理，设计系统(1)在a=35，b=3，c=28，h=20 时的电路，如图2 所示。电路中的运算放大器型号为TL084CN，乘法器型号为AD633(增益为1)，电源电压值为12 V，其余电路元件参数值见图2。

根据图2 所示的电路图进行电路实验，分别在输出端口接入示波器，得Multisim 仿真相图如图3，这与图1 的Matlab 数值仿真结果一致。

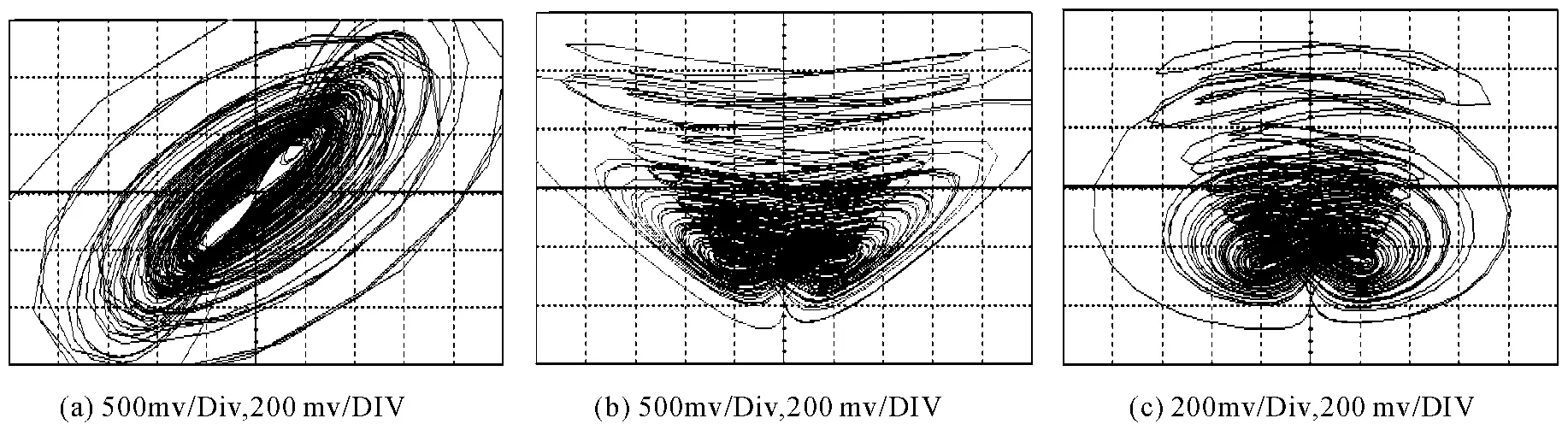
图3 系统(1)混沌电路原理

3 线性反馈同步下的保密通信及电路

3.1 混沌系统在保密通信中的应用

混沌系统的1 个重要概念是混沌同步与控制，混沌电路的1 个重要应用是混沌保密通信。混沌系统的同步控制是20 世纪末人们在混沌系统中发现的1 个重要特征。他对应于自然界广泛存在的共振、锁模现象［2］，利用了混沌的1 个重要特征——遍历性。这里基于线性反馈同步控制［9］思想进行保密通信的研究。

发射系统和接收系统分别为:

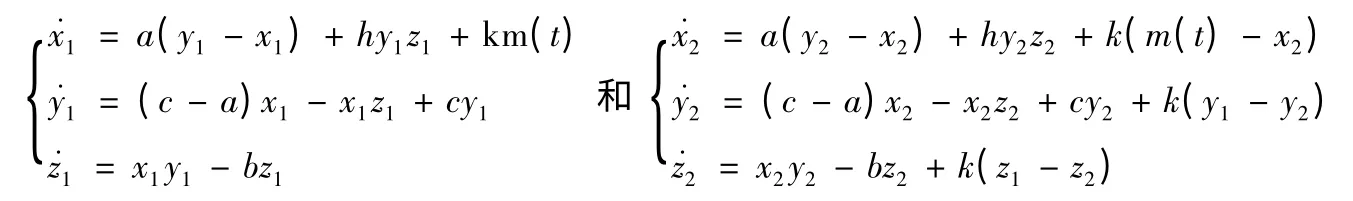
其中:s(t)=m(t)-x1表示信道中传输的信号;m(t)表示要传输的有用信号，以比混沌信号小得多的强度调制在混沌信号中。在s(t)的驱动下，发射系统与接收系统的混沌信号可近似同步，即x1≈x2，在接收端通过混沌同步提取信号

这里k=1，选取有用信号为三角波，Matlab 仿真结果如图4 所示。由图4 可以看出，传送的信号得到了接收系统的有效恢复。

图4 三角波信号在混沌保密通信系统下的传输

3.2 混沌系统的保密通信电路

根据以上分析，可设计出系统(1)的保密通信电路，如图5。

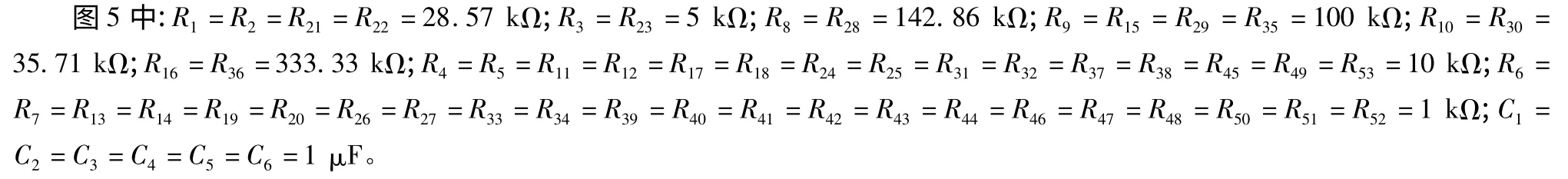
图5 保密通信电路原理

根据图5 所示的电路进行实验，接入示波器后，可得到原系统的Multisim 仿真图像，如图6。通过观察可发现，图4 与图6的仿真结果一致，达到了混沌掩盖的目的。

图6 三角波信号在保密通信系统下的传输

4 结束语

本文在1 个混沌系统的基础上，通过线性反馈同步控制法构造出了1 个保密通信电路。该方法理论简单，易于实现，又因混沌系统具有遍历性、内随机性和分维性等复杂特征，这就进一步增加了信号破译的难度。

［1］朱清祥，张蕊.陈氏混沌系统的混沌同步［J］.武汉理工大学学报，2008，30(3):348-358.

［2］陈关荣，吕金虎.Lorenz 系统族的动力学分析、控制与同步［M］.科学出版社，2005:11-19.

［3］王晓燕，瞿少成，田文汇.异结构混沌系统同步及其在保密通信中的应用［J］.计算机应用研究，2009，26(5):1874-1876.

［4］An XL，Yu JN，Zhang JG，et al.A new multistage chaos synchronized system for secure communications［C］//2009 Fifth International Conference on Natural Computation.Washington DC:IEEE Computer Society，2009:437-441.

［5］胡爱花，徐振源，李芳.复杂网络连接的Chen 系统的同步化［J］.系统科学与数学，2007，27(2):302-313.

［6］Lee T H，Park J H.Generalized functional projective synchronization of Chen-Lee chaotic systems and its circuit implementation［J］.International Journal of the Physical Sciences，2010，5(7):1183-1190.

［7］Pehlivan I，Uyaroglu Y，gun M Y.Chaotic oscillator design and realizations of the Rucklidge attractor and its synchronization and masking simulations［J］.Scientific Research and Essays，2010，5(16):2210-2219.

［8］张国山，牛弘.一个基于Chen 系统的新混沌系统的分析与同步［J］.物理学报，2012，61(11):1-11.

［9］王发强，刘崇新.Liu 混沌系统的线性反馈同步控制及电路实验的研究［J］.物理学报，2006，55(10):5055-5059.