基于OSVR的谷氨酸发酵过程建模

韩顺成， 潘 丰， 李艳坡

(江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122)

谷氨酸［1］发酵过程具有较强的非线性和时变性，建立其机理模型较为困难，而复杂的机理模型也不易用于控制和优化。因此，建立一个精确有效的黑箱模型对谷氨酸发酵生产过程具有重要意义。

支持向量机(SVM)是基于结构风险最小原则和统计学理论的机器学习方法之一。SVM能较好地解决小样本、非线性、过学习、维数灾难和局部极小等问题，具有很强的泛化能力，目前已经广泛应用于模式识别、回归估计、概率密度估计等各个领域。M．Martin和J．S．Ma在Ger提出的支持向量机分类(Support Vector Machine Classification，SVC)在线算法［2］的基础上，提出了支持向量机回归(Support Vector Machine Regression，SVR)［3-4］在 线 算 法。OSVR(Online Support Vector Machine Regression)是一种先进的SVM训练方法，WANG等［5］运用标准的OSVR对谷氨酸发酵过程建模，实现了对于菌体质量浓度、基质质量浓度和产物质量浓度的在线建模。实验结果表现出良好的泛化能力并降低了模型的预测误差，优于基于神经网络(Neural Network)和SVM模型。但是研究发现在标准的OSVR算法中，由于核函数是非线性的，计算核函数需要大量的训练时间，增加了算法的计算量;并且核函数的数据并非在每一步中都被更新，且被更新的数据仅仅占据了一小部分。

因此，为了提高算法运算速度和预测精度，文中利用缓存保存核函数，将其核函数矩阵进行相应调整，对OSVR进行改进。文中应用改进的OSVR对谷氨酸进行模型建立，并在仿真软件Matlab上，与标准的OSVR进行比较。结果表明，基于改进的OSVR算法建立的谷氨酸动力学模型表现出良好的精确性，并提高了算法的在线学习速度。

1 改进的在线支持向量机回归

给出一训练集:T={(xi，yi)，i=1，2，…，l}，yi∈R和x∈RN，可以构造线性回归函数［6］:

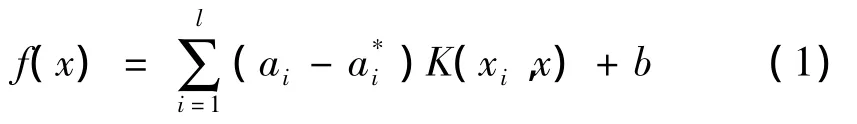
式中:l为训练集T中样本个数;ai，a为拉格朗日因子;K(xi，x)= φ(xi)·φ(x)为核函数;φ(xi)为非线性映射将数据xi映射到高维特征空间。

ai和b可以通过求解以下优化函数得到:

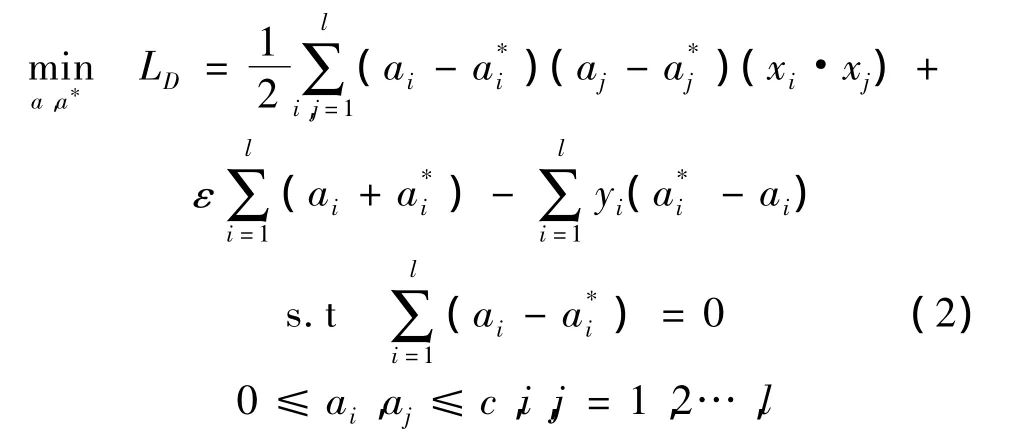
通过拉格朗日因子和 Karush-Kuhn-Tucke(KKT)条件［7］(具体推导过程参见文献［4］)，训练数据可以分为:

1)错误的支持向量集合E:

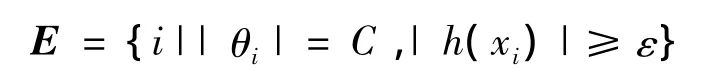
2)边缘支持向量集合S:

S={i|0 ＜|θi|＜ C，|h(xi)|= ε}

3)保留的支持向量集合R:

R={i||θi|=0，|h(xi)|≤ ε}

当增加一个新的样本xc至训练集T中，初始令θc=0，为使xc进入E，R，S其中一个集合中，并同时满足KKT条件，必须满足以下等式:

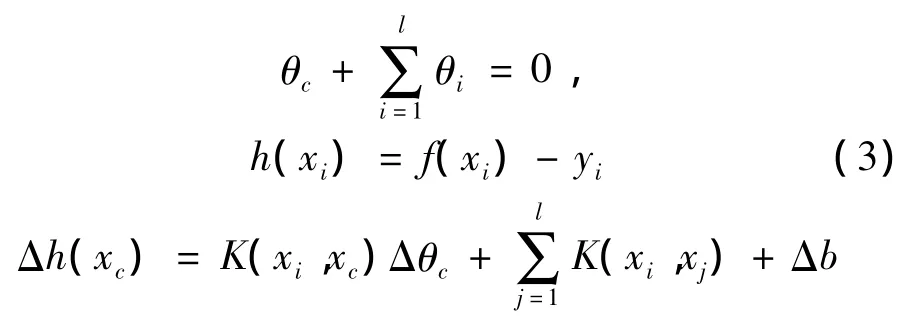
标准的OSVR算法［5］中，由于核函数是非线性的，计算核函数浪费了大量的训练时间，增加了算法的计算量;并且关于核函数的数据并非都被更新在每一步中，被更新的数据仅仅占据了一小部分。为了提高算法运算速度，用一个核矩阵K(xn，xG)来表示 K(xn，xE)，K(xn，xR)和 K(xn，xS)。此时 K(xn，xG)，K(xn，xc)可表示为

xGi∈ G，i=1，2，…，ln，ln是E ∪ R∪S∪c集合中样本的数目。G是E，S，R 3个集合中的其中一个。

当增加一个样本xc:

当移除一个样本xc:

在xc被增加或者被移除时，其余的某些样本可能被从原本的集合中更新至另外一个集合中，在每步更新过程中，一些样本会被从一个集合更新另一个集合中。当一样本xGli从集合G1更新至G2内时，有以下4种可能更新情况:

Case 1:G1=R，G2=S;Case 2:G1=S，G2=R;Case 3:G1=E，G2=S;Case 4:G1=S，G2=E。

在每一种情况下，矩阵 K(xn，xG1)，K(xn，xG1i)和K(xn，xG2)的相应更新情况分别如下:

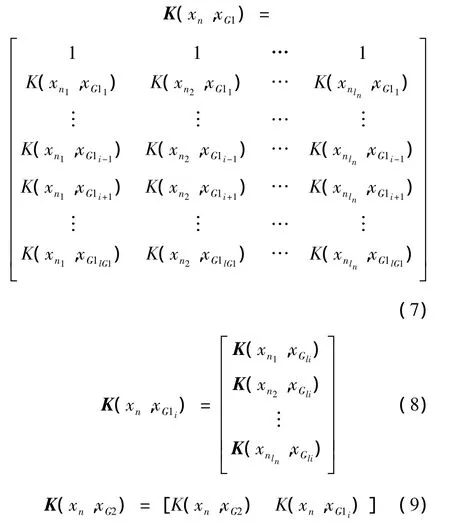
增量算法:当一个样品被增加至训练样本集，通过逐渐改变θc，直到xc进入R，S，E 3个子集的一个，这个过程中一些其他的样品也从G1更新至G2，通过计算和更新 K(xn，xG1)，K(xn，xG1i)，K(xn，xG2)来确保其他样本仍满足KKT条件。

减量算法:当一个样本的θc为零时，由于该样本不影响支持向量机模型;在式(4)的前提下，改变θc和h(xc)，当xc样本被移除时，使得剩余其他样本仍继续满足KKT条件。

上述是通过核函数矩阵进行处理改进OSVR算法，其算法的有效性将在下面进行验证。

2 基于改进的OSVR谷氨酸模型

谷氨酸是一种重要的氨基酸物质，主要采用补料分批发酵方法生产。影响发酵过程的可在线测量变量主要有温度、通气流量、pH值、溶解氧质量浓度DO、补料量等，这些参数密切相关谷氨酸质量浓度。根据发酵机理的过程，文中选择温度xT(i)、pH值xpH(i)、溶氧质量浓度xDO(i)和尾气CO2排放量xCO2(i)作为输入变量的谷氨酸质量浓度软测量模型。温度、pH值、溶氧质量浓度和尾气CO2排放量在线数据通过相应传感器获取，谷氨酸的质量浓度由SBA-40B生物传感仪(山东省科学院生物研究所生产)测定。选取第i+1次谷氨酸质量浓度xG(i+1)作为输出预测量。

详细的动力学模型建立过程如下:

1)构建一个OSVR训练样本集X{Xi=(xTi，xpHi，xCO2i，xDOi，xGi)}，总计有 l个样本。

2)当增加一个新样本xc，初始化θc=0，并计算 K(xn，xE)，K(xn，xR)，K(xn，xs)，K(xn，xc);

3)利用增量算法对样本训练:(1)If|h(xc)|≤ε，xc→ R，并更新 K(xn，xR);(2)当一个样本被更新从G1→G2中时，通过式(8)，(9)，(10)计算出相应的K(xn，xG1)，K(xn，xG1i)，K(xn，xG2);

4)当训练样本数目溢出值max_sp=l，利用减量算法移除多余样本;

5)计算训练误差e=xG(i+1)－xG(i)(xG(i+1)表达式，参考公式(11)，当e≤min_error，训练停止，否则继续3);

6)用该模型预测xG(i+1)。

OSVR算法一旦确定，就可以对变量进行预测，由式(1)可得基于支持向量回归机软测量的谷氨酸模型如下:

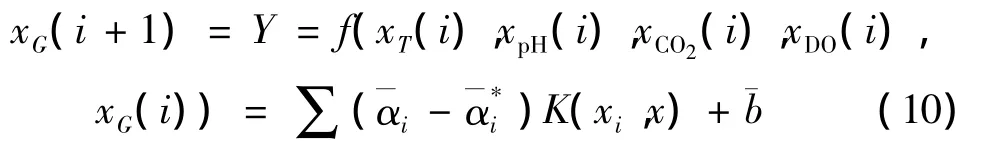
这里选用 RBF 核函数［8］，即

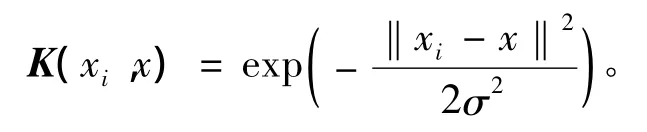
支持向量机中σ，C，ε等参数的选取直接影响到训练结果。因此文中通过交叉算法经多次实验选取:σ =0．6，C=100，ε =0．1，此时训练效果为最佳，可确保建模具有优良的预测性能。均方误差

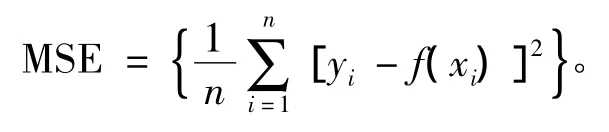
文中的数据来自某实验室提供由5 L发酵罐生产谷氨酸所获得的10批次正常发酵数据，每批数据表达一个完整的谷氨酸发酵过程。每批分为15个样品。7个批次数据作为训练数据，其余的作为测试数据。仿真计算机为Intel(R)Celeron(R)CPUE330，1 024 M内存，仿真软件为Malabr2010a。

可以得到谷氨酸质量浓度的预测结果，与实际测量值的比较如图1所示。

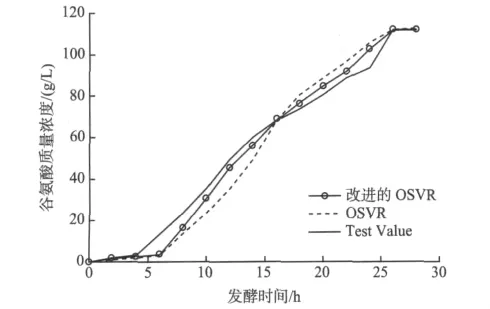
图1 基于改进的OSVR的谷氨酸质量浓度预测曲线Fig．1 Prediction curve based on the improved OSVR glutamate concentration

图1显示基于改进的OSVR的谷氨酸动力学模型与测试值比较表现出较好的拟合效果，尤其在发酵过程10 h后，优于OSVR。为了验证该模型具有较强的泛化能力，采用预测误差值来比较模型的精确度，预测误差值可以用相对误差的形式表示:

基于改进的OSVR相对误差如图2所示。

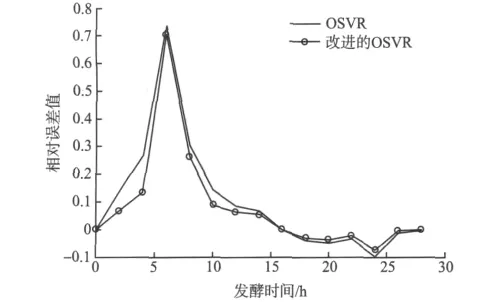
图2 基于改进的OSVR的相对误差Fig．2 Relative error based on of the improved OSVR

表1中的训练时间，改进的OSVR是3个方法之中速度最快的，且均方差MES最小。图1，2和表1，显示基于改进的OSVR谷氨酸动力学模型获得了良好的泛化能力，表现出最优的训练精度，其谷氨酸预测模型表现出良好的精确性，与此同时提高了算法的训练速度，取得了改进算法的预期效果。以上显示谷氨酸产物质量浓度获得了良好的预测精度，在保证良好精度的前提下，并提高了建模过程的运行速度，对谷氨酸实际生产具有一定参考价值。

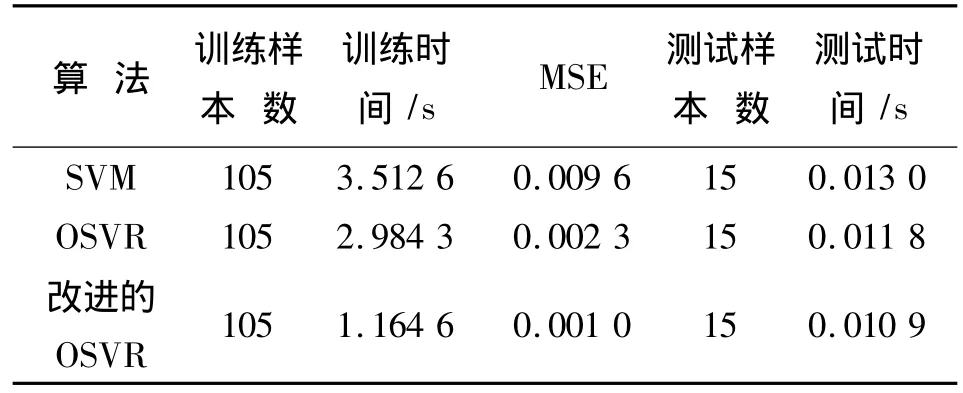
表1 训练时间、测试时间和MSE比较Tab．1 Comparison of training time， testing time and MSE

3 结语

近年来随着生物技术工业迅速发展，生物发酵过程建模已获得了高度的关注，由于缺乏可靠的传感器用于过程变量的在线检测等原因，其自动化水平与其他工业生产过程相比还较低。因此，一个精确的在线模型对减少发酵原材料和动力消耗、提高产物生产量具有重要意义。

微生物发酵具有高度的非线性和时变性，其内在机理复杂。在线支持向量机是一种较好的估计预测手段。基于在线支持向量机的模型具有较高的精度，该模型泛化能力强，动态性能好，能较好地描述实际对象的特性，该模型可用于发酵过程中状态变量的估算与预测。

［1］Kinoshita S，Udaka S．Shimono studies on the amino acid fermentation-Part I．Production of L-glutamic acid by various microorganisms［J］．Journal of General and Applied Microbiology，1957，3:193-205．

［2］ Gert Cauwenberghs，Tomaso Poggio．Incremental and decremental support vector machine learning［J］．In Advances Neural Information Processing Systems(NIPS’2000)［J/OL］．http://books．nips．cc/papers/files/nips13/CauwenberghsPoggio．pdf

［3］Martin M．Online support vector machines for function approximation，Technical Report LSI-02-11-R［R］．Software Department，Universitat Politecnica de Catalunya，Spain，2002．

［4］MA J S，James T，SimonP．Accurate on-line support vector regression［J］．Neural Compuing，2003，15(11):2683-2704．

［5］WANG X，DU Z，PAN F．Dynamic modeling of biotechnical process based on online support vector machine［J］．Journal of Computers，2009，4(3):251-258．

［6］邓乃扬，田英杰．数据挖掘中的新方法-支持向量机［M］．北京:科学出版社，2004．

［7］Takahashi N，Guo J，Nishi T．Global convergence of SMO algorithm for support vector rgression［J］．IEEE Trans on Neural Networks，2008，19(6):971-982．

［8］Smola A J，Scholkopf B．Learning with Kernels［M］．Cambridge，MA:MIT Press，2001．