n个幂等矩阵线性组合的幂等性
崔润卿,李幸兰
(河南理工大学 数学与信息科学学院,河南 焦作 454003)
n个幂等矩阵线性组合的幂等性
崔润卿,李幸兰
(河南理工大学 数学与信息科学学院,河南 焦作 454003)
给出了当 P1,P2,…,Pn是n个不同的、非零的、两两可交换的 m×m幂等矩阵,并且c1,c2,…,cn是非零复数时,线性组合 P=c1P1+c2P2+…+cnPn在两两乘积等于零与两两乘积等于其中一个的条件下仍为幂等矩阵的一组充分条件。
幂等矩阵;线性组合;幂等性
0 引言
一些特殊矩阵线性组合的幂等性问题在概率统计中有着重要的应用[1-2]。 近年来,2个、3个以及4个幂等矩阵的线性组合仍然是幂等矩阵的问题被很多国内外学者所研究[3-10]。2000年,Baksalary和Baksalary[1]给出了两个幂等矩阵的线性组合仍为幂等矩阵的充要条件。之后关于幂等矩阵线性组合的研究有很多,并且已经延伸到了投影、广义投影和超广义投影的线性组合[2-3]。2004年,Baksalary[2]给出了3个非零幂等矩阵P1、P2、P3满足P2P3=0=P3P2线性组合的幂等性的刻画。之后Ozdemir和Ozban[7]给出了3个非零的两两可交换的幂等矩阵线性组合的幂等性的一些充分条件。2005年,王月清等[8]给出了3个幂等矩阵线性组合的幂等性的一些充分条件,推广了文献[1]的结果。2010年,谢涛[9-10]给出了3个和4个幂等矩阵线性组合的幂等性的另一组充分条件。本文应用更为简便的方法研究了n个幂等矩阵线性组合的幂等性的充要条件,给出了更为一般的结果。
设C是复数集,Mn(C)表示C上所有阶方阵构成的集合。F⊆Mn(C )表示Mn(C)中所有两两可交换的非零幂等矩阵构成的集合。设 c1,c2,…,cn∈C{0},P1,P2,…,Pn∈F。本文的主要工作是讨论
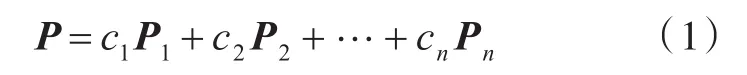
是幂等矩阵的一组充分条件。
1 主要结果及证明
定义1 P∈Cn×n,若 P2=P,则称 P为幂等矩阵。
定理 1 设 P1,P2,…,Pn∈F ,令 γ=(c1,c2,…,cn),其中c1,c2,…,cn∈C{0},Pi≠0,PiPj= PjPi(i,j=1,…,n),P=c1P1+c2P2+…+cnPn,当PiPj=Pi(i,j=1,…,n,i≤j),且
(i)若 n为偶数,则当 γ=(c1,c2,…,cn)= (-1,1,-1,…,1)时,P为幂等矩阵。
(ii)若 n为奇数,则当 γ=(c1,c2,…,cn)= (1,-1,1,…,1)时,P为幂等矩阵。
证明 P=c1P1+c2P2+…+cnPn,若P为幂等矩阵,则P2=P,即

将(2)式的系数写成矩阵形式,有

(3)式中:
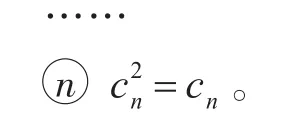
(i)若 n为偶数,则当 γ=(c1,c2,…,cn)= (-1,1,-1,…,1) 时,
把 γ=( c1,c2,…,cn)=(-1,1,-1,…,1 )代入(3)式,变为

即P为幂等矩阵。
(ii)若 n为奇数,则当 γ=(c1,c2,…,cn)= (1,-1,1,…,1)时,P为幂等矩阵。
把 γ=(c1,c2,…,cn)=(-1,1,-1,…,-1)代入(3)式,变为

定理1证毕。
推 论 1 设 P1,P2,…,Pn∈F ,c1,c2,…,cn∈C{} 0 ,Pi≠0,PiPj=PjPi(i,j=1,…,n),n为偶数,P=c1P1+c2P2+…+cnPn,当P1Pj=P1,PiPj=Pj(i≤j,i≠1),且 γ=(c1,c2,…,cn)= ( -1,1,-1,…,1)时,P为幂等矩阵。
推 论 2 设 P1,P2,…,Pn∈F ,c1,c2,…,cn∈C{} 0 ,Pi≠0,PiPj=PiPj(i,j=1,…,n),n为奇数,P=c1P1+c2P2+…+cnPn,当 P1Pj=P1,PiPj=Pj(i≤j,i≠1),且 γ=(c1,c2,…,cn)= (1,-1,1,…,1)时,P为幂等矩阵。
[10]中的结果可由定理1的结论作为n=4时推出。
对参考文献[10]中定理1进行推广。
当 n为奇数时,线性组合的系数为 γ=(1,-1,1,…,1),其中有n+个1,n个-1,对其进行排列组合,共有+12种情况,其中每一种排列组合通过定义PiPj=Pi或 PiPj=Pj又有n个充分条件,则共有n·+12个充分条件。同样,当n为偶数时,线性组合的系数为γ=(-1,1,-1,…,1),里面有个1,个-1,对其进行排列组合,共有种情况,每一种排列组合通过定义 PiPj=Pi或 PiPj=Pj又有n个充分条件,则共有n·C个充分条件。
定 理 2 设 P1,P2,…,Pn∈F ,c1,c2,…,cn∈C{0},Pi≠0,PiPj=PjPi(i,j=1,…,n),P=c1P1+c2P2+…+cnPn,当 PiPj=0(i≠j),且() c1,c2,…,cn=(1,1,…,1)时,P为幂等矩阵。
证明 因为PiPj=0,i≠j,则
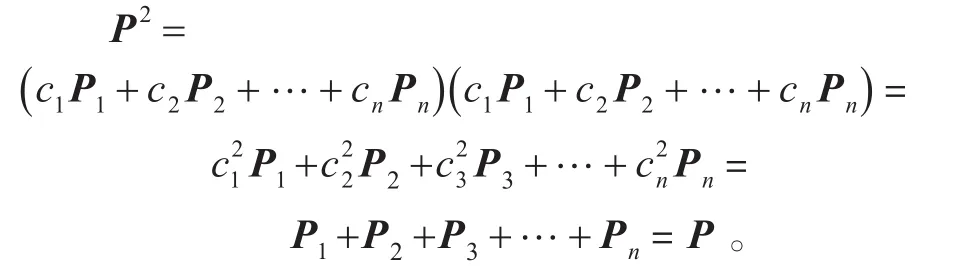
定理2证毕。

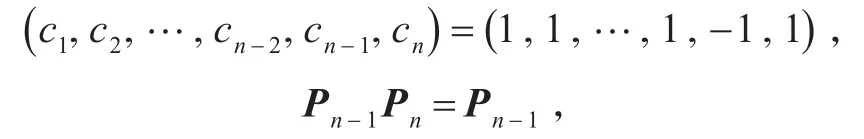
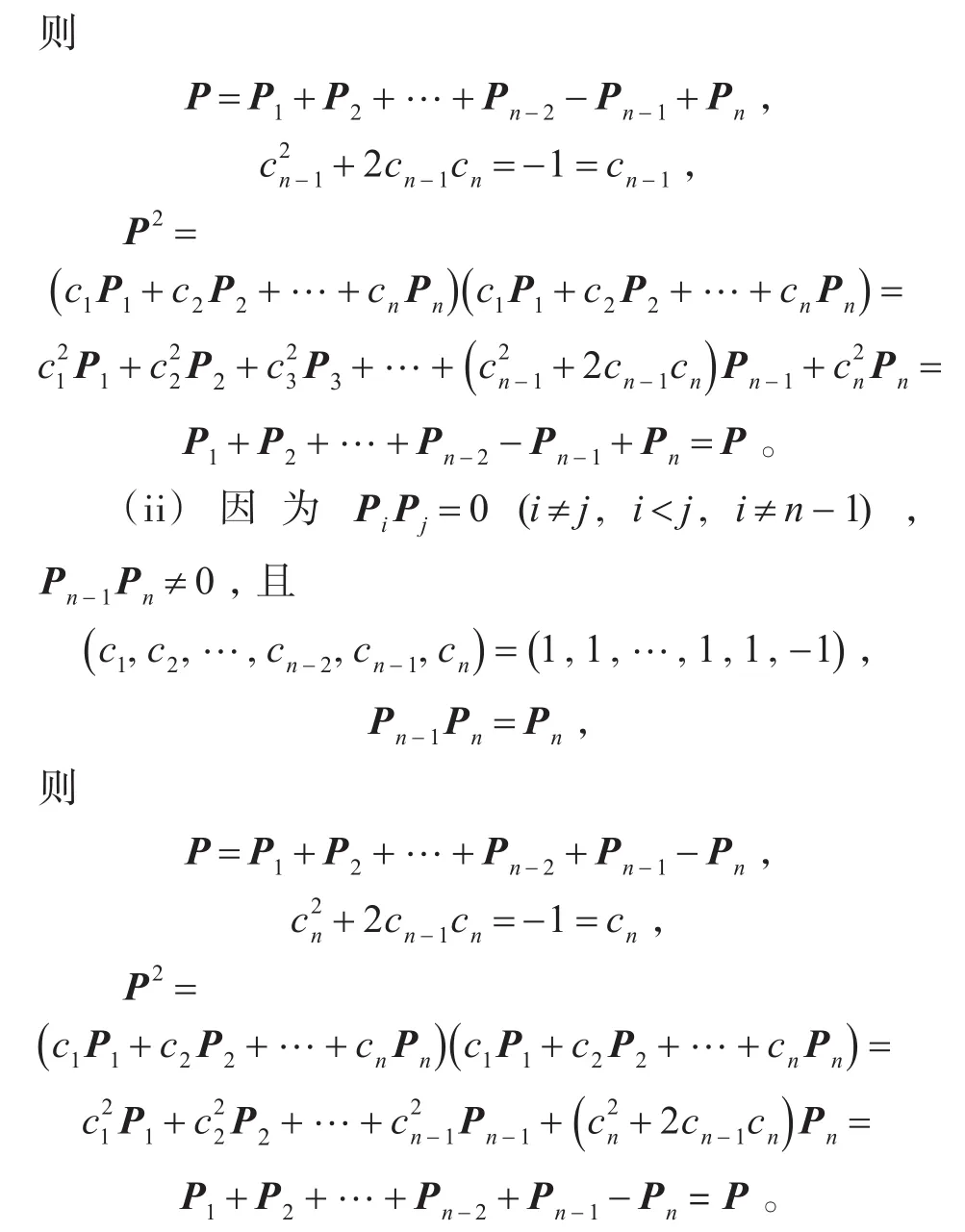
定理3证毕。
注 定理3解决了n个两两可交换非零幂等矩阵的线性组合,在两两乘积只有一个不为0,其余全为零条件下(1)式的幂等性的充分条件。
参考文献:
[1] Baksalary J K,Baksalary O M.Idemoptency of linear combinations of three idempotent matrices[J].Linear Algebra Appl,2000,321:3-7.
[2] Baksalary O M.Idemoptency of linear combinations of three idempotent matrices,two of which are disjoint[J].Linear Algebra Appl,2004,388:67-68.
[3] Baksalary J K,Baksalary O M,Styan G P H.Idemop⁃tency of linear combinations of an idempotent matrix and a tripotent matrix[J].Linear Algebra Appl,2002,354:414-418.
[4] Benitez J,Thome N.Idemoptency of linear combina⁃tions of an idempotent matrix and t-potent matrix and commute[J].LinearAlgebra Appl,2004,403:414-418.
[5] Baksalary O M,Benitez J.Idemoptency of linear combi⁃nations of three idempotent matrices,two of which are commuting[J].LinearAlgebraAppl,2007,424:320-337.
[6] Horn R A,Johnson C R.Matrices analysis[M].Cam⁃bridge:Cambridge University Press,1991.
[7] Ozdemir H,Ozban A Y.On idempotency of linear com⁃binations of idempotent matrices[J].Applied Mathemat⁃ics and Computation,2004,159:439-448.
[8] 王月清,王爱丽.3个幂等矩阵线性组合的幂等性[J].宝鸡文理学院学报:自然科学版,2005,25(3):166-167.
[9] 谢涛.关于3个幂等矩阵线性组合的若干探讨[J].宝鸡文理学院学报:自然科学版,2010,30(1):11-13.
[10]谢涛.四个幂等矩阵线性组合的幂等性[J].湖北师范学院学报:自然科学版,2010,30(4):15-18.
Idempotency of Linear Combination ofnIdempotent Matrices
CUI Run-qing,LI Xing-lan
(School of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo 454003,Henan,China)
LetP1,P2,…,Pnbendifferent nonzero mutually commutativem×midempotent matrices andc1,c2,…,cnbe nonzero complex number,a set of sufficient conditions are given for the matrixP=c1P1+c2P2+…+cnPnstill to be an idempotent matrix under the condition that the mutual product is zero or the mutual product is equal to either one.
idempotent matrix;linear combination;idempotency
O151.21
:A
:1673-0143(2013)02-0007-03
(责任编辑:强士端)
2012-12-16
河南省高等教育教学改革研究省级立项项目(2012SJGLX125)
崔润卿(1966—),男,副教授,研究方向:矩阵分析。

