岩石超声谐波特征及其随应力的变化

郭志伟,葛洪魁,谢 凡,张金伟,刘政一

(1.中国地震局地球物理研究所地震观测与地球物理成像重点实验室,北京 100081； 2.中国石油大学非常规天然气研究院,北京 102249)

岩石超声谐波特征及其随应力的变化

郭志伟1,葛洪魁2,谢 凡1,张金伟1,刘政一1

(1.中国地震局地球物理研究所地震观测与地球物理成像重点实验室,北京 100081； 2.中国石油大学非常规天然气研究院,北京 102249)

岩石具有较强的非均质性和强衰减特性,谐波测量的难度较大。建立超声谐波测试实验系统,采用单频脉冲串(tone burst)激发、门控放大、脉冲反转和叠加等增强二次及高次谐波,研究岩石超声谐波的发育与振幅特征,定义名义非线性系数,分析单轴应力下岩石超声谐波及名义非线性系数随应力的变化。结果表明,超声谐波包含了丰富的岩石内部结构信息,表征了岩石的非线性特性,利用先进的仪器系统,采用谐波强化技术,可有效地获得岩石的超声谐波及其振幅,进行岩石非线性特性、微结构变化与损伤演化的监测。

地球物理学；岩石物理；岩石特性；超声谐波；应力；非线性系数；脉冲反转

材料损伤早期监测在材料性能和安全评价方面具有重要的用途,其中一项重要的技术是基于超声谐波的非线性超声监测,因其对介质内部微结构高度敏感性而引起广泛关注。Eular等[1]最早提出流体中的非线性波动理论,后来,Breazeale等[2-3]研究了晶体和金属材料中的非线性现象。之后,非线性谐波[4-5]、共振频率漂移[6-7]、非线性滞后现象[8]、次谐波[9]等复杂的非线性现象受到了广泛关注。Sony Baby[10]、Kim[11]等通过实验证明了非线性谐波方法在检测金属材料早期损伤方面的有效性。曾星[12]对单向拉伸至不同塑性形变的标准45#钢试样进行了超声非线性测量。陈小佳[13]采用超声高阶谐波和超声调制两种方法,定量观测到了碱骨料反应下试件从初始微裂出现、发展和连通等不同阶段的全过程损伤演化的过程。周正干等[14]认为连续脉冲串激励较大振幅的超声波,使材料内部不连续处受迫振动,随声波周期“闭合”或“张开”,使时域波形畸变,频域表现为出现谐波,产生非线性响应。岩石具有矿物颗粒边界、孔隙裂隙发育等微结构特征,具有丰富而复杂的非线性现象[15]。相应地通过监测岩石非线性现象可以反映岩石微结构的变化,而达到检测岩石损伤的目的[16-17],对地震孕育、地质灾害、建筑物安全等问题具有重要意义。岩石具有较强的非均质性和强衰减特性,谐波测量的难度较大。笔者针对岩石超声谐波测试的难点,发展谐波增强技术,研究岩石超声谐波的发育与振幅特征及其随应力的变化。

1 非线性与超声谐波

线性超声检测声波振幅很小,应力-应变的关系可用线性关系近似,对介质内部微小裂隙的发育和介质局部性质变化不敏感。随着激发超声波振幅的增加,在介质中产生的应变场扰动加剧,应力-应变不再满足线性假设,运动方程中的二阶项甚至更高阶项不能再被忽略。细杆中应力和应变的关系可表示为

式中,σ、ε和E分别表示正应力、正应变和一阶弹性系数(杨氏模量)；β为二阶非线性弹性系数,通常简称为非线性系数。

现假设最简单的细杆中的声传播情况,单一频率的正弦纵波u=A0cos(ωt)从介质一端入射,在另一端接收,并且忽略波传播过程中的衰减,那么平面纵波在超声传播方向上的一维波动方程为

式中,ρ为传播介质密度；x为超声波传播距离；u为质点振动位移。

结合式(1)、(2)并考虑粒子振动位移和应变的关系,得到关于质点振动位移的非线性波动方程

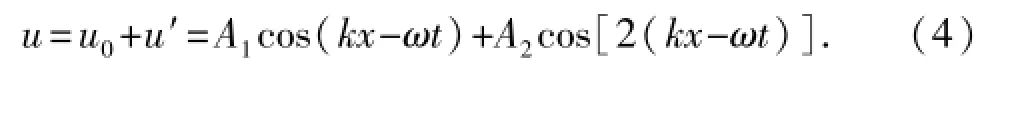
求解近似到二阶,其中u0为线性方程解,u′为一次微扰解,代表非线性解。A1为接收端基频(激发频率)的振幅,A2为产生的二次谐波振幅,由非线性系数β决定,满足

其中k=2π/λ为超声波波数,λ为超声波波长。

相应地,非线性系数β可通过测量接收端基频和二次谐波的振幅并计算得到:

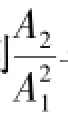
同理可得到三阶非线性系数β2与三次谐波振幅的关系[4]:

当在介质中同时激发两组频率不同的正弦波时,还将产生这两组波相互作用相互调制的频率成分[5]。

2 岩石超声谐波测试

通常二次和更高次谐波相对于基波振幅很小,往往淹没在系统和环境噪声中,加之岩石是一种典型的不均匀介质,超声在岩石中传播时会发生散射和强衰减,波场复杂,谐波测试难度很大。一方面要求仪器系统(包括激发和接收传感器、信号激发和接收系统等)具有很高的性能、低仪器自噪声、微弱信号检测能力,另一方面需要发展一些谐波增强技术。

2.1 实验系统

实验装置如图1所示。本实验使用Ritec RAM-5000(R5000)激发超声波信号。激发探头采用Olympus Panametric A101s 0.5 MHz超声探头,该探头具有性能良好的阻尼设计,可有效地抑制压电陶瓷换能器的自由振动,使电信号转换成超声信号时不发生严重畸变。实验以监测二次谐波特征为主要目的,使用中心频率1 MHz、直径为15 mm、厚度为3 mm的铌酸锂压电陶瓷晶片为接收探头。实验中激发探头和接收探头使用耦合剂粘附于测试样品两侧,再用水杨酸苯酯固定,并用松紧带加固。接收探头接收到的信号经20 dB前置放大器放大后,由高精度的数据采集器进行数字化记录,并与R5000的同步输出信号进行时间同步,同步精度10-9s。数据采集器采样率为20 MHz。实验样品为粗粒花岗闪长岩,样品为圆柱形,直径50 mm,长110 mm。实验中改变激发电压,从几十伏到几百伏线性增强,研究谐波随激发信号强度的变化,并分析非线性系数的变化。

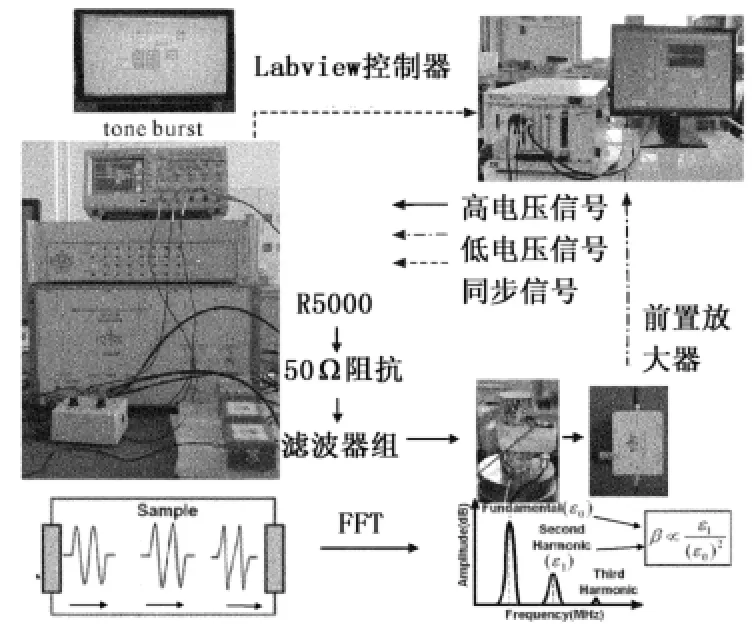
图1 岩石超声谐波实验系统Fig.1 Experimental system of ultrasonic harmonics in rock

介质的超声谐波是高阶小量,谐波检测属于频率域微弱信号检测,对仪器性能要求很高,如激发信号的频率、相位精确控制,大功率激发、高性能滤波、探头信号高保真等。由R5000输出的高压电信号,经50Ω的低阻抗匹配和低通滤波器,减少电子电路可能会造成的高频噪声。激发和接收探头经过阻尼设计,可有效地抑制压电陶瓷换能器的自由振动,实现高保真激发与接收。

2.2 单频脉冲激发

实验中通过改变激发脉冲信号振幅(激发电压),改变接收信号基波和谐波信号幅度,从而获得超声谐波随激发信号强度的变化特征,研究岩石非线性特性变化。在超声波信号激发方面,激发信号的高能量和单频性,有助于高次谐波信号的观测。测试时,由R5000激发频率0.5 MHz的大功率正弦波列(单频脉冲串,射频激发RF,tone burst)见图2。大能量激发信号有利于谐波检测,激发信号能量随激发电压和波列长度的增大而增大,波列周期数根据样品长度确定,周期数乘以波长小于样品的长度,以防止入射波和样品边界反射波叠加而产生复杂的波场,影响谐波测试[11]。

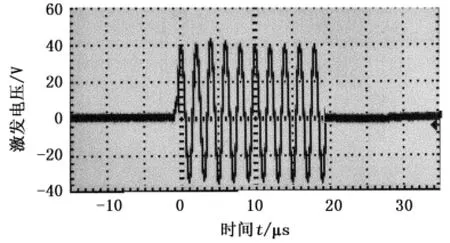
图2 R5000激发的大功率正弦波列Fig.2 Tone burst with high power excited by R5000

2.3 脉冲反转技术

由式(4)可知,当激发信号相位变化180°时,接收的基频信号相位也变化180°,但是二次谐波的相位却保持不变。因此,可通过两次激发相位相差180°的信号(脉冲反转),将得到的两次接收信号进行叠加来抑制基频信号,提高二次谐波信号的信噪比,增强谐波的测量精度[11,18]。图3所示为采用脉冲反转检测结果(激发频率0.5 MHz)。可以看出脉冲反转技术有效地抑制了基频信号,突出了二次谐波。

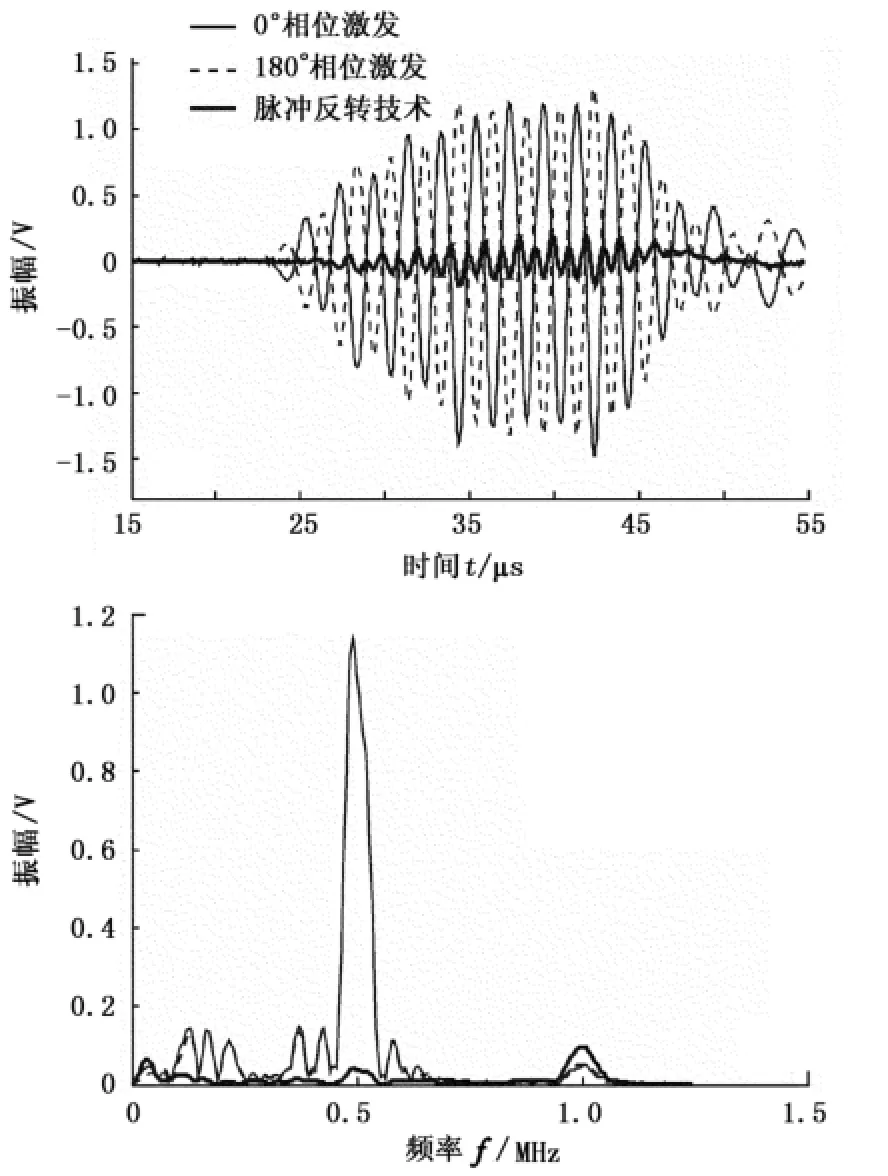
图3 脉冲反转技术示意图Fig.3 Sketch map of pulse inversion technique

2.4 信号叠加与处理方法

同相信号的叠加可以抑制随机噪声,提高信噪比。实验中采用脉冲反转技术,在某一激发电压下,用信号发生器分别激发0°和180°的两个相位的信号,每个信号激发256次,叠加得到两条反相位激发的高信噪比信号。用矩形窗分别截取这两条信号的直达波部分,矩形窗长度等于激发信号持续时间。然后用快速傅里叶变换技术得到截取信号的振幅谱,在激发频率的周围分别取最大振幅值再求平均得到基频振幅。将接收得到的0°和180°两个相位信号相加,用矩形窗截取直达波部分,并在截取信号振幅谱中求二次谐波频率附近的最大值,除以2得到二次谐波的振幅。

2.5 相对振幅测量和名义非线性系数

接收探头接收到的信号幅度受多种因素影响,严格来说,实验的每一个环节从信号发生器、门控放大器到激发-接收探头,再到探头与样品的耦合方式,都可能影响接收信号的幅度。激发-接收探头的频率响应特征是影响测量系统的重要因素。共振型探头可强化特定频率的信号。当以检测二次谐波为主,接收探头的共振频率是激发探头共振频率的二倍,接收信号中基频、三次甚至更高次谐波同样可以接收但振幅受到抑制。考虑到对于特定频率信号的探头频响校正为简单的线性关系,接收探头的共振性不会影响基频和谐波振幅比的特征关系。因此使用共振型探头测量的基频和谐波振幅是“相对值”。这种相对振幅测量并不影响振幅比的特征关系。将由相对振幅测量得到的“非线性系数”称为“名义非线性系数”。“名义非线性系数”可用于材料性质变化的动态监测,求取“非线性系数”绝对值需进行探头的频响等多方面校正。

另外,探头与岩石之间的耦合也是影响非线性系数绝对值测量的重要因素。耦合情况主要影响探头与岩石之间界面的反射和透射,增加了接收信号的绝对幅值的测量难度。图4为5次探头与岩石耦合测试结果。可以看到耦合情况对测量的基频和谐波振幅有较明显的影响。但这种影响同时作用于基频和谐波成分,而使得基频与谐波的振幅比不受影响。实验得到A2/A21的耦合误差在1.5%以内。

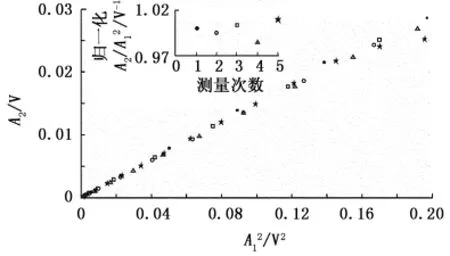
图4 探头与岩石样品的耦合对非线性系数的影响Fig.4 Variation of nonlinear coefficient with coupling between sensors and rock

3 岩石超声谐波特征

实验中通过改变激发电压,研究不同激发强度下的谐波特征及谐波振幅变化,并分析名义非线性系数的变化。图5为粗粒花岗闪长岩测量结果。从图中可以看到超声波高次谐波的发育特征。当激发电压较低时(如22和42 V),接收信号只含有激发频率0.5 MHz成分,运用脉冲反转技术叠加后,基本为白噪声信号,超声谐波不发育。随着激发电压的增加,接收信号出现频率为1 MHz的二次谐波信号。脉冲反转激发相加的结果大大压制了基频成分,强化了二次谐波,提高了二次谐波测量的可靠性和精度。当激发电压继续增加到280 V时,接收信号中出现明显的三次谐波成分。虽然接收探头的频响特征在一定程度上压制了三次谐波信号的振幅,但是无法阻止三次谐波振幅随着激发电压的增加而增加的趋势,同时测量的二次谐波却逐渐减小。由此推测三次谐波不仅包含基频成分在非线性介质中传播产生的三次谐波,同时也包含由基频信号和二次谐波信号相互作用、相互调制而出现的三次谐波信号。也就是说,随着激发电压的增加,一部分二次谐波能量由于非线性作用而分配到三次谐波中,导致二次谐波振幅的减小。从图5中还可以看到,四次谐波成分伴随三次谐波出现在脉冲反转处理后的信号中,这种伴生关系也与谐波间的相互调制有关。因此,三次和四次谐波的产生不但与岩石非线性有关,也与不同频率的谐波调制有关,当然谐波调制也是材料的非线性特征之一。

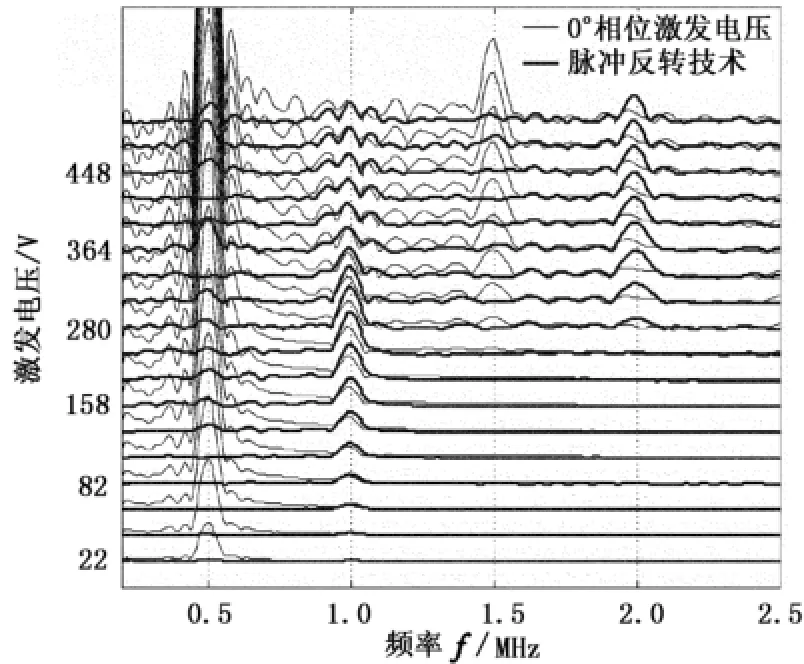
图5 接收信号直达波频谱随激发电压的变化Fig.5 Variation of spectrum of received signals with different exciting voltages

图6定量地分析了二次谐波、三次谐波的振幅相对于基频振幅的变化(图中,圆点或方框的大小表示激发电压的相对高低)。当激发电压小于280 V时,二次谐波振幅与基频振幅的平方表现为较好的线性关系,表明在此激发水平下主要发育二次谐波,岩石介质的非线性主要来自于弹性模量的二阶小量,三次谐波不发育。当激发电压达到280 V及以上时,二次谐波振幅偏离与基频振幅的平方关系,并且出现随激发电压的增加而减小的趋势,三次谐波开始发育显著,其振幅随着激发电压的增加而快速增加,并与基频振幅的立方保持稳定的线性关系。最小二乘拟合280 V激发电压以下的二次谐波与基频振幅的关系为280 V以上激发电压的三次谐波与基频振幅的关系为

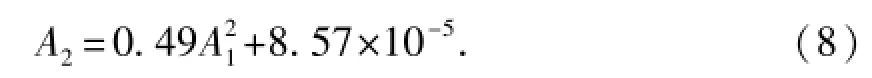
在经典非线性理论下,三次谐波远比二次谐波弱。但是本实验中,由高能量(＞280 V)激发的三次谐波振幅远超过二次谐波,是岩石中存在的非经典非线性现象之一。Johnson等[15]在研究灰岩、砂岩等岩石样品的非线性谐波时也发现了类似的非经典非线性现象。在三次谐波与基频振幅立方的线性关系中,较大的直线截距也表明三次谐波的产生机制已不同于经典非线性理论。但是三次谐波振幅仍与基频振幅的立方保持较好的直线关系,间接表明此时三次谐波在一种较稳定的机制下形成。对超声谐波发育特征的分析可知超声波穿过粗粒花岗闪长岩时,其非线性行为随着激发能量的增加,由经典非线性向非经典非线性转变。

4 岩石超声谐波特征随应力的变化

在单轴加载过程中对岩石的超声谐波特征进行了测试,一方面验证本文提出的测量方法的有效性,另一方面探索谐波在岩石性质及其变化研究中的应用。实验以测量岩石在某一应力状态下的名义非线性系数为基本手段,研究不同应力状态下名义非线性系数的变化特征。使用MTS 100 t试验机以75 kPa/s的速度对花岗闪长岩样品加载至96 MPa,再以相同的速度卸载至0 MPa。在这一过程中每加载或卸载2.5 MPa沿径向测量一次谐波及其幅度,实验结果如图7所示。

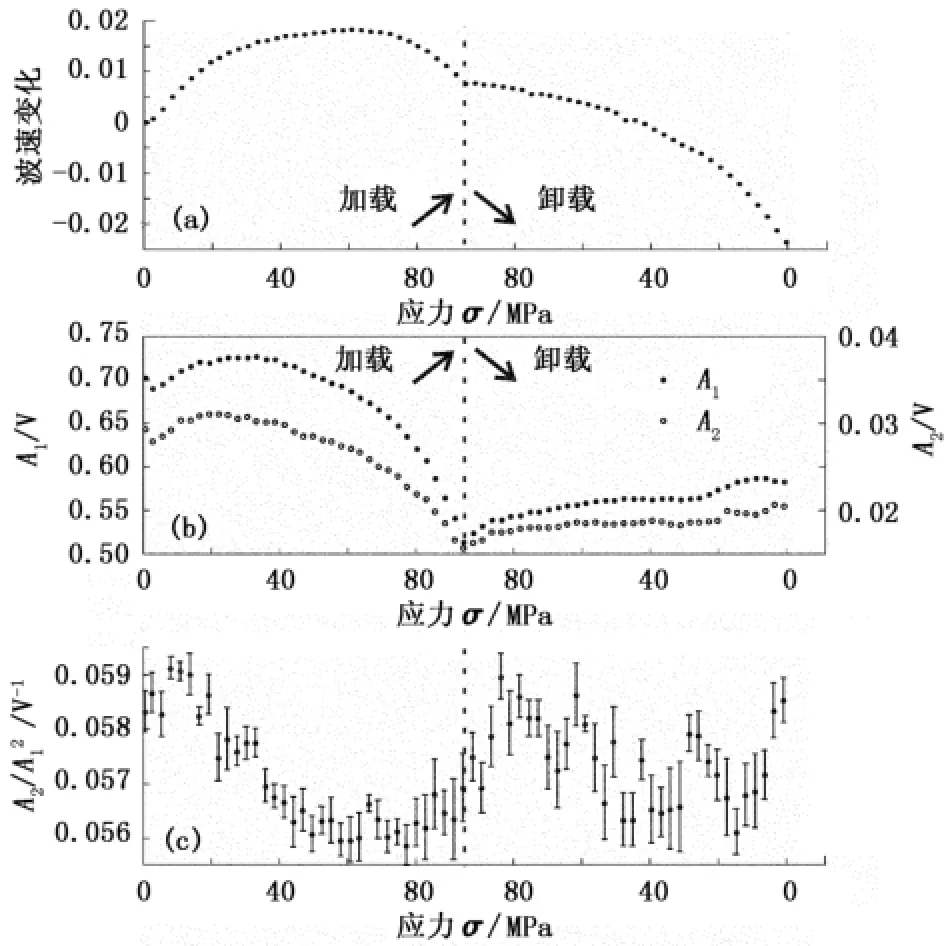
图7 岩石尾波波速变化、谐波幅值及名义非线性系数随载荷的变化Fig.7 Variation of coda-wave velocity,harmonics amplitude and nominal nonlinear coefficient with loading

图7(a)为利用尾波干涉测量获得的径向波速相对变化,是一种岩石状态的显示[19-21]。表明直到60 MPa,岩石一直处于加载强化,之后进入加载弱化。图7(b)为超声激发电压为30 V时基频与二次谐波振幅随加/卸载的变化,相同激发电压和实验条件下,卸载信号幅度比加载小很多,表明加载过程中样品内部诱发了微裂隙；加载过程中基频和二次谐波幅度都经历了先增大后减小的过程,代表着加载过程中的原有裂隙的闭合和新裂隙(膨胀)的产生。而卸载过程中基频和谐波幅度逐渐增大,与加载过程中发育的裂隙轴向优势方位分布有关(图8)。轴向卸载使轴向裂隙开度减小,径向超声基波和谐波幅度增大。

图7(c)为二次谐波振幅与基频振幅平方的比值在加/卸载过程中的变化,在测量系统稳定的情况下反应了非线性系数的变化。在加载过程中,非线性系数表现为先减小后增加的特征,与岩石加载时经历的裂隙闭合的压实阶段和裂隙扩展的膨胀阶段大致对应。非线性系数的变化与岩石内部微结构的变化有关。在卸载初期,非线性系数继续保持一段时间的增加趋势,有可能是因为卸载初期岩石仍处于高应力状态,仍有相当部分的裂隙继续生长,而导致非线性增强。随着应力的持续降低,非线性呈现出较不稳定的特征,同时二次谐波振幅与基频振幅的平方关系的拟合误差也增加。在一定程度上说明岩石非线性行为的不稳定性。这种不稳定的非线性行为可能与岩石内不同方向的裂隙的张开闭合的不均匀性和临界失稳有关。

图8 粗粒花岗闪长岩加载形成轴向优势分布裂隙Fig.8 Primary distribution of cracks orientation from fractured coarse-grained granodiorite

从图7还可以看出,加载过程中非线性系数与波速变化有相似的变化趋势,二者均在60 MPa附近达到极值,之后进入加载弱化阶段。实际上,单位应力作用下引起的波速相对变化也是一种非线性系数的度量[20]。而基频和谐波幅度随应力变化的峰值应力(30 MPa)与非线性系数存在较大差别,说明幅度的变化与非线性系数的控制因素有所不同,这种不同可提供更细致深入的岩石微结构信息。

5 结 论

(1)超声谐波是岩石重要的非线性特征,包含了丰富的岩石内部结构信息,可利用岩石的超声谐波,进行岩石非线性特性、微结构变化与损伤演化的监测研究。

(2)采用单频脉冲串(tone burst)高能激发、门控滤波、脉冲反转和叠加等能增强二次及高次谐波,实现二次及更高次谐波的有效观测。

(3)岩石超声谐波与基波振幅(激发电压)有关,当激发电压较低时,超声谐波不发育。随着激发电压的增加,接收信号出现二次谐波,二次谐波振幅与基频振幅的平方成较好的线性关系。当激发电压继续增加到更高值时,接收信号中出现三次和四次谐波,三次谐波与基频振幅的立方成线性关系。三次和四次谐波的产生不但与岩石非线性有关,也与不同频率的谐波调制有关。

(4)单轴应力下花岗闪长岩谐波幅值及名义非线性系数随载荷而变,反映了岩石内部微裂隙的演化,与岩石加载时经历的裂隙闭合、扩展大致对应。

[1] 王润田,章瑞铨,周艳,等.非线性声学的进展与应用[J].声学技术,2007,26(2):348-357.

WANG Run-tian,ZHANG Rui-quan,ZHOU Yan,et al. Progression and application of the nonlinear acoustics [J].Technical Acoustics,2007,26(2):348-357.

[2] BREAZEALE M A,FORD J.Ultrasonic studies of the nonlinear behavior of solids[J].J Appl Phys,1965,36 (11):3486-3490.

[3] ZAREMBO L K,KRASILıNIKOV V A.Nonlinear phenomena in the propagation of elastic waves in solids[J]. Sov Phys Usp,1971,13(6):778-797.

[4] NA J,BREAZEALE M A.Ultrasonic nonlinear properties of lead zirconate titanate ceramics[J].J Acoust Soc Am,1994,95(6):3213-3221.

[5] VAN DEN ABEELE K E A,JOHNSON P A,SUTIN A. Nonlinear elastic wave spectroscopy(NEWS)techniques to discern material damage,part 1:nonlinear wave modulation spectroscopy(NWMS)[J].Res Nondestr Eval, 2000,12(1):17-30.

[6] VAN DEN ABEELE K E A,CARMELIET J,TEN CATE J A,et al.Nonlinear elastic wave spectroscopy(NEWS) techniques to discern material damage,part2:single mode nonlinear resonance acoustic spectroscopy[J].Res Nondestr Eval,2000,12(1):31-42.

[7] PAYAN C,GARNIER V,MOYSAN J.Potential of nonlinear ultrasonic indicators for nondestructive testing of concrete[J].Advances in Civil Engineering,2010,ID 238472.

[8] GUYER R A,MCCALL K R,BOITNOTT G N.Hysteresis,discrete memory,and nonlinear wave propagation in rock:a new paradigm[J].Phys Rev Lett,1995,74 (17):3491-3495.

[9] SOLODOV I Y,KROHN N,BUSSE G.CAN:an example of nonclassical acoustic nonlinearity in solids[J].Ultrasonics,2002,40:621-625.

[10] BABY S,KOWMUDI B N,OMPRAKASH C M,et al. Creep damage assessment in titanium alloy using a nonlinear ultrasonic technique[J].Scripta Materialia, 2008,59:818-821.

[11] KIM J Y,JACOBS L J,QU J,et al.Experimental characterization of fatigue damage in a nickel-base su-peralloy using nonlinear ultrasonic waves[J].J Acoust Soc Am,2006,120(3):1266-1273.

[12] 曾昱.超声非线性的理论与实验研究[D].北京:北京交通大学土木建筑工程学院,2008.

ZENG Yu.Theoretical and experimental studies of nonlinear ultrasonic[D].Beijing:School of Civil Engineering in Beijing Jiaotong University,2008.

[13] 陈小佳.基于非线性超声特征的混凝土初始损伤识别和评价研究[D].武汉:武汉理工大学交通学院, 2007.

CHEN Xiao-jia.Study on initial damage detection and evaluation of concrete base on nonlinear acoustic features [D].Wuhan:School of Transportation in Wuhan University of Technology,2007.

[14] 周正干,刘斯明.非线性无损检测技术的研究、应用和发展[J].机械工程学报,2011,47(8):2-11.

ZHOU Zheng-gan,LIU Si-ming.Nonlinear ultrasonic techniques used in nondestructive testing:a review[J]. Journal of Mechanical Engineering,2011,47(8):2-11.

[15] JOHNSON P A,ZINSZNER B,RASOLOFOSAON P N J.Resonance and elastic noninear phenomena in rock [J].J Geophy Res,1996,101(B5):11553-11564.

[16] PASQUALINI D,HEITMANN K,TEN CATE J A,et al.Nonequilibrium and nonlinear dynamics in Berea and Fontainebleau sandstones:low-strain regime[J].J Geophy Res,2007,112,B01204.

[17] ZINSZNER B,JOHNSON P A,RASOLOFOSAON P N J.Influence of change in physical state on elastic nonlinear response in rock:significance of effective pressure and water saturation[J].J Geophy Res,1997,102 (B4):8105-8120.

[18] VERBEEK X A A M,LEDOUX L A F,WILLIGERS J M,et al.Experimental investigation of the pulse inversion technique for imaging ultrasound contrast agents [J].J Acoust Soc Am,2000,107(4):2281-2290.

[19] 宋丽莉,葛洪魁,郭志伟,等.利用多次散射波监测介质性质变化的试验研究[J].岩石力学与工程学报, 2012,31(4):713-722.

SONG Li-li,GE Hong-kui,GUO Zhi-wei,et al.Experimental study of variation of media properties monitoring using multiple scattering waves[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(4):713-722.

[20] 宋丽莉,葛洪魁,梁天成,等.小应力扰动下岩石弹性波速变化的波形检测[J].中国石油大学学报:自然科学版,2012,36(4):60-65.

SONG Li-li,GE Hong-kui,LIANG Tian-cheng,et al. Waveform detection of elastic wave velocity changes in rock under small stress perturbations[J].Journal of China University of Petroleum(Edition of Natural Science),2012,36(4):60-65.

[21] 梁天成,葛洪魁,郭志伟,等.利用声发射和波速变化判定岩石损伤状态[J].中国地震,2012,28(2): 154-166.

LIANG Tian-cheng,GE Hong-kui,GUO Zhi-wei,et al. Evaluation of rock damage state with acoustic emission and velocity variation[J].Earthquake Research in China,2012,28(2):154-166.

(编辑 修荣荣)

Ultrasonic harmonic characteristic in rock and its variation with stress

GUO Zhi-wei1,GE Hong-kui2,XIE Fan1,ZHANG Jin-wei1,LIU Zheng-yi1

(1.Key Laboratory of Seismic Observation and Geophysical Imaging,Institute of Geophysics,
China Earthquake Administration,Beijing 100081,China；
2.Unconventional Natural Gas Institute in China University of Petroleum,Beijing 102249,China)

The strong heterogeneity and strong attenuation in rocks make ultrasonic harmonic measurement more difficult.An experimental system for observing the ultrasonic harmonic was established.The measurement resolution of high harmonic waves was improved through the tone burst excitation,high power gated amplifier,pulse inversion technique and stacks of many repeated measurements.The growth and intensity of ultrasonic harmonic waves were discussed,the nominal nonlinear coefficient was defined,and the variations of harmonic characteristics and the nominal nonlinear coefficient with stress in rocks were investigated.The results show that ultrasonic harmonic includes the abundant information on rock internal structure,and represents the nonlinearity of the rocks.By the advanced instruments and harmonic reinforcement techniques,ultrasonic harmonic and its amplititude can be effectively measured,and the damage evolution and the variations of nonlinearity and microstructure in loaded rocks can be monitored.

geophysics；petrophysics；rock properties；ultrasonic harmonic；stress；nonlinear coefficient；pulse inversion technique

P 313.1

A

1673-5005(2013)03-0050-07

10.3969/j.issn.1673-5005.2013.03.008

2013-02-10

国家自然科学基金项目(41174040)；中央级公益性科研院所基本科研业务费专项(DQJB11B 11；DQJB11C04)；中国石油大学(北京)引进人才科研启动基金项目(YJRC-2012-03)

郭志伟(1986-),男,博士研究生,主要从事岩石物理实验研究。E-mail:gzwave2312@163.com。