采用耦合电感的交错并联电流临界连续Boost PFC变换器输入差模EMI分析

杨 飞 阮新波 季 清 叶志红

（1.南京航空航天大学航空电源重点实验室 南京 210016 2.光宝科技股份有限公司 南京 210019）

1 引言

交错并联的Boost PFC 变换器既保留了单路Boost 电路高功率因数、高效率和低成本的优点，又可以降低输入和输出的电流脉动，逐渐成为近年来的研究热点[1-3]。对于Boost 变换器中的多个独立电感，类似多路交错并联Buck 变换器中的输出电感耦合[4-6]，也可以进行磁性元件的集成和耦合[7-9]。文献[8]较早地对工作于电流临界连续模式（Critical Current Mode，CRM）的交错并联Boost PFC 变换器电感耦合做了分析，但主要集中于磁性元件集成；文献[9]指出两路交错并联的CRM Boost PFC 变换器的电感反向耦合后，可以降低电感的匝数，但是输入电流的脉动增加，可能影响前级差模（Differential Mode，DM）电磁干扰（Electromagnetic Interference，EMI）和滤波器的设计，为此本文做了进一步分析。

经典的差模滤波器设计方法需要确定变换器的最恶劣干扰频谱，通过与电磁干扰标准比较得到滤波器需要的衰减频谱。利用滤波器的衰减曲线逼近需要的衰减频谱，得到满足标准限制的滤波器最小转折频率，进而确定滤波器元件的参数[10]。当开关频率恒定时，差模干扰的频谱是离散的，干扰值主要出现在开关频率及其倍数次频率处，最恶劣频谱一般在最低输入电压的满载时，较易确定；当开关频率变化时，如CRM，开关频率和脉动电流幅值随着输入电压和输入功率的变化而变化，差模干扰频谱是连续的且变化规律较复杂[11]，所以最恶劣频谱较难确定。同时，由于EMI 接收机对干扰电压的处理不是简单的傅里叶分解，进行EMI 分析需要大量的电路仿真和实际测试。为此，人们对EMI 接收机进行了数学建模[11-14]，基于接收机模型计算给定频率的EMI 干扰值，进而得到不同输入电压和输入功率下的EMI 干扰频谱，便于直接分析电磁干扰的变化规律，确定最恶劣的频谱，

本文采用已有的EMI 接收机数学模型，计算电感耦合前后交错并联CRM Boost PFC 变换器的差模传导电磁干扰频谱，分析最恶劣干扰频谱的规律。基于数学上电流脉动幅值和干扰值的关系，提出一种简单的预测最恶劣频谱出现条件的方法。最后测试了一台300W的交错并联Boost PFC 变换器。

2 采用耦合电感的交错并联CRM Boost PFC 变换器

2.1 耦合对等效电感的影响

图 1 为采用反向耦合电感的交错并联 CRM Boost PFC 变换器，其中vin为输入电压，vg为整流后的输入电压，Vo是输出电压。iL1和iL2分别为流过两个电感绕组的电流，L1和L2分别为两个电感绕组的自感值，M是两个电感绕组的互感值。

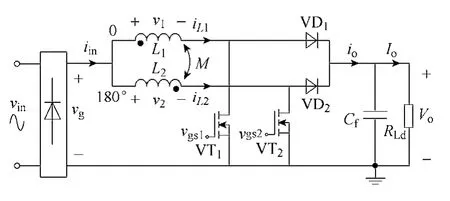
图1 两路交错并联Boost PFC 变换器Fig.1 Two-phase interleaved Boost PFC converter

从图1 中可得两个电感绕组上的电压为

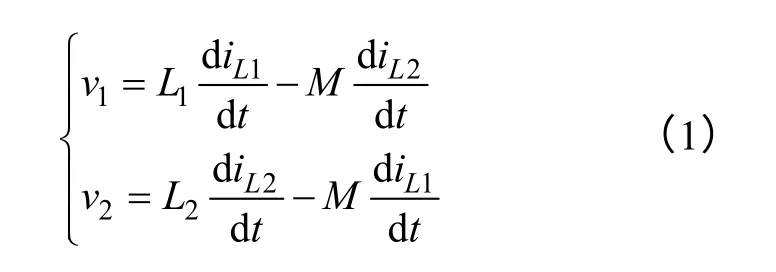
假设耦合电感两个绕组是对称的，有L1=L2=Lcp。定义耦合系数α=M/Lcp。每个开关周期内占空比满足

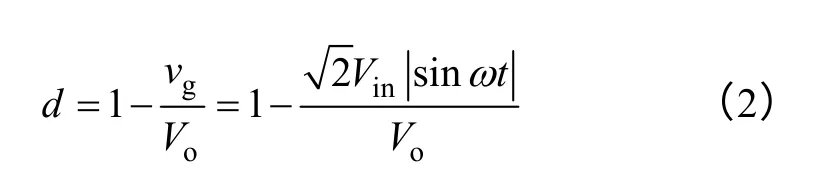
式中，Vin为输入电压有效值；ω为输入电压角频率。

图2 为开关周期内，d＜0.5 和d＞0.5 时变换器的主要波形，其中不同开关模态时的等效电感表达式为[9]

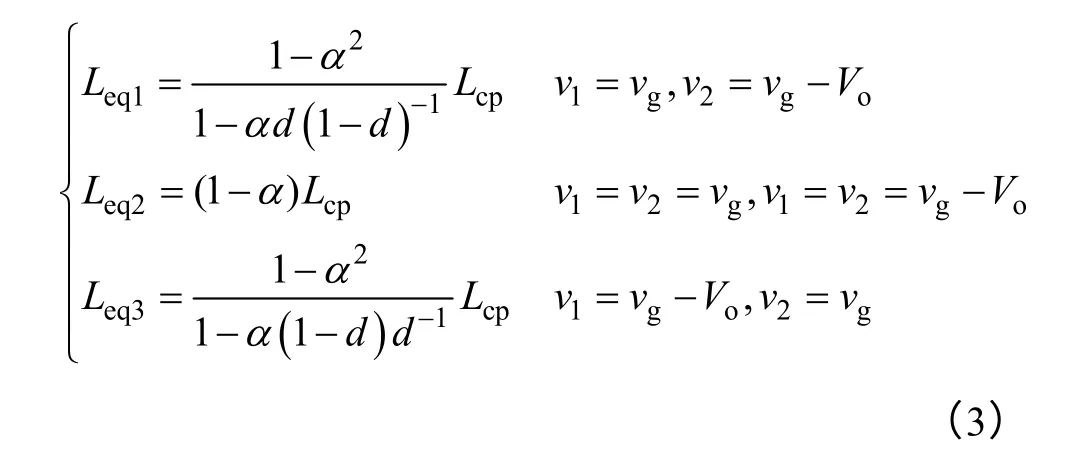
由图2 可以看出，Leq2决定输入电流脉动值，且由式（3）可知，Leq2的大小与占空比无关，只与耦合系数和自感值有关。Leq1和Leq3分别决定d＜0.5和d＞0.5 时每路电感绕组电流的峰值，即脉动值，其随占空比的变化如图3 所示。当d＜0.5 时，Leq1随着d的增大而增大；当d＞0.5 时，Leq3随着d的增大而减小。耦合越强，越靠近d=0.5的等效电感值越大，越靠近d=0 或d=1的等效电感值越小。

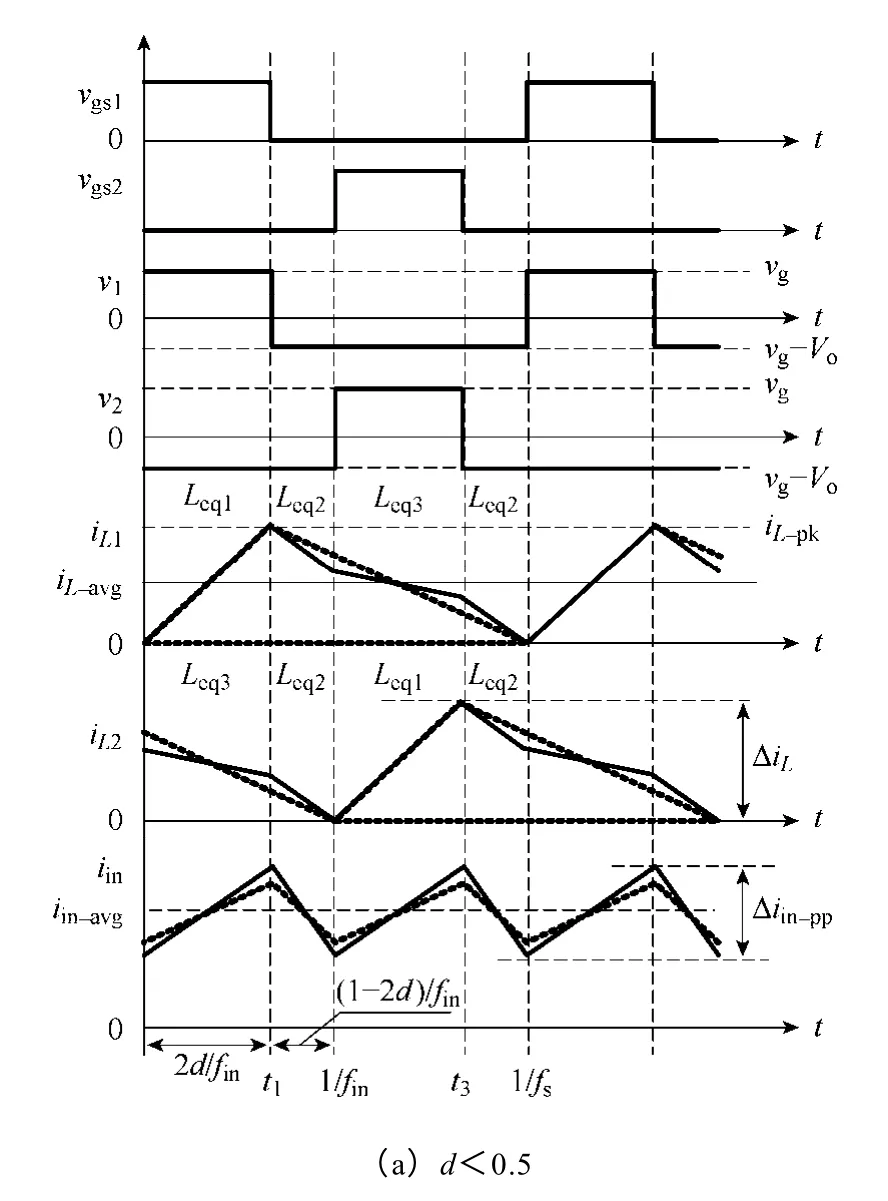
图2 采用耦合电感的交错并联CRM Boost PFC 变换器主要波形Fig.2 Key waveforms of two-phase interleaved CRM boost PFC converter with coupled inductor

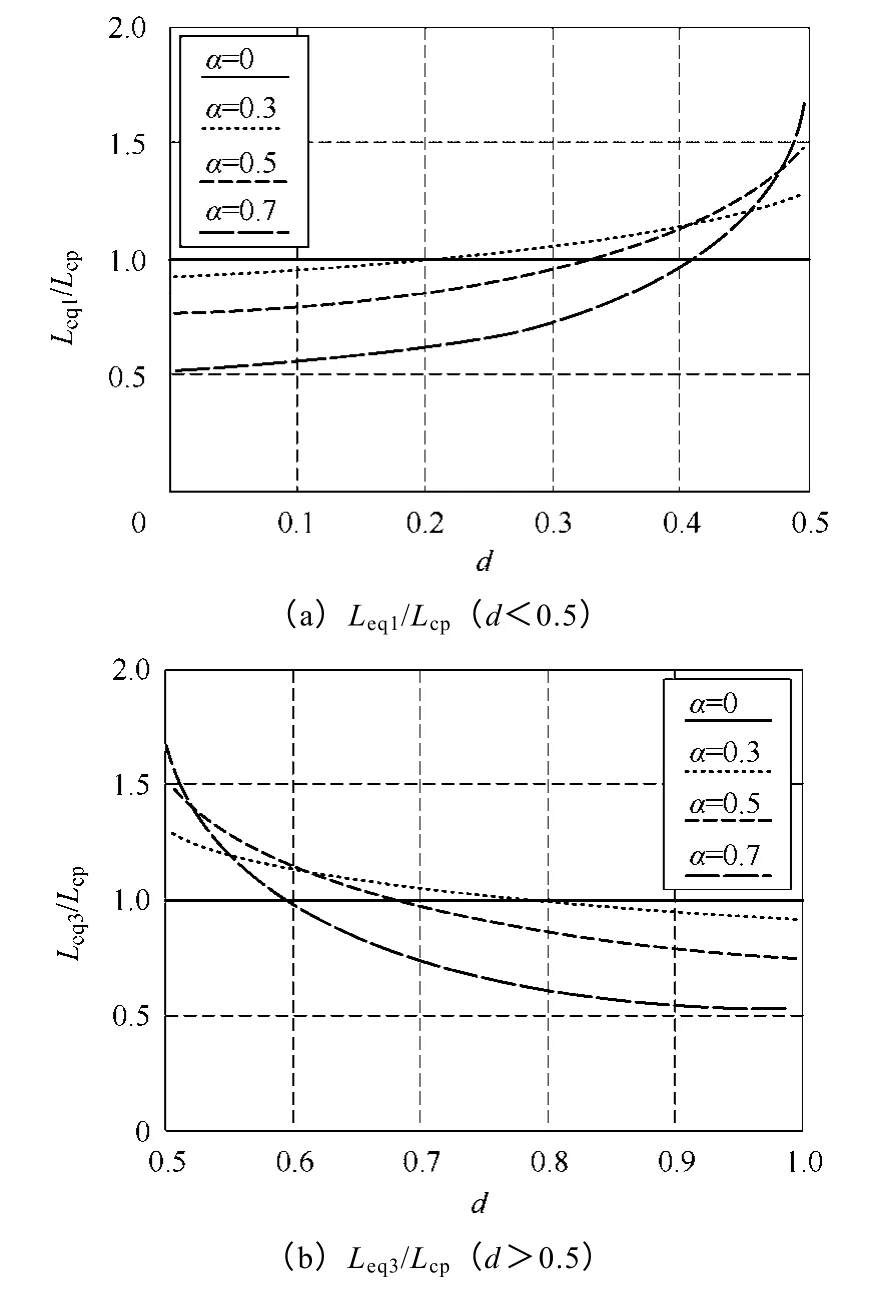
图3 不同耦合系数下等效电感值与占空比的关系曲线Fig.3 Equivalent inductance varied with duty cycle in different coupling coefficients

2.2 输入电流脉动的频率

在图2a 所示的一个开关周期内，每路电感绕组电流的平均值等于其峰值的一半[9]。若变换器总输入功率为Pin，则每路Boost 电路分担Pin/2的功率，电感电流峰值iL_pk和平均值iL_avg的表达式为

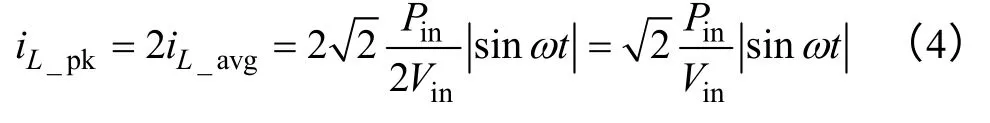
由于CRM的电感电流脉动即电感电流峰值由输入电压和输入功率决定，所以耦合前后是不变的[9]。

当d＜0.5 时，图2a 中开关管的导通时间为

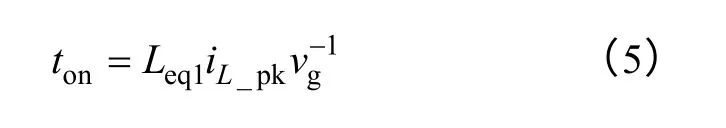
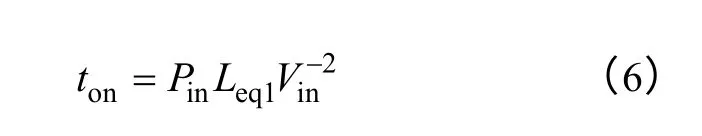
则开关频率的表达式为

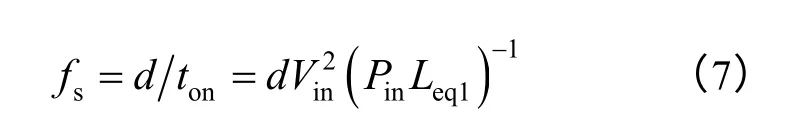
当d＞0.5 时，图2b 中开关管的关断时间为

将式（4）和vg=2Vinsinωt代入式（8），得

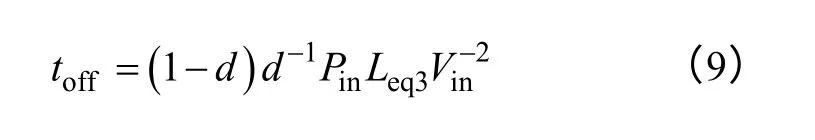
则开关频率fs表达式为

若两路理想交错180º，输入电流脉动的频率fin是开关频率的两倍，将式（3）代入式（7）和式（10）得

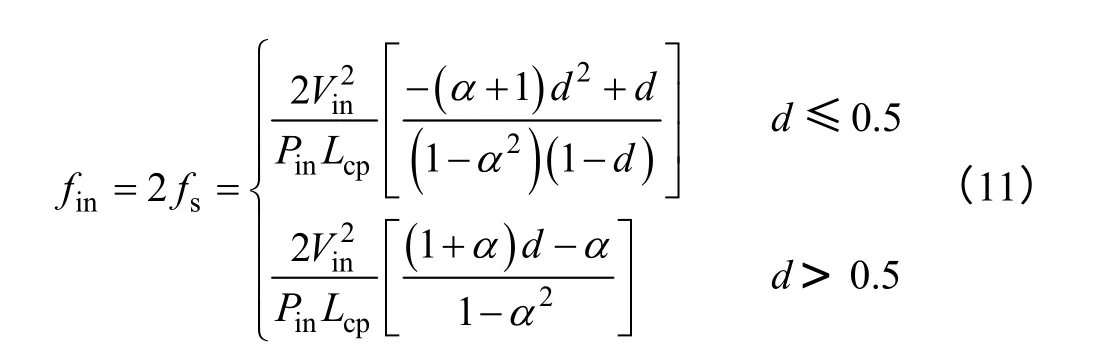
若耦合前后Lcp不变，在给定输入电压和输入功率时，不同耦合系数时fin随着占空比的变化曲线如图4 所示。若电感不耦合（α=0），则fin随占空比的增加而增加。电感耦合后，由于接近d=0.5 时的等效电感值增加，此处fin降低；在接近d=0 和d=1时等效电感值降低，此处fin增加。

图4 不同耦合系数下fin 与占空比的关系曲线Fig.4 Input current ripple frequency varied with duty cycle in different coupling coefficients

2.3 输入电流脉动的幅值

图2 中的输入电流脉动幅值Δiin_pp可表达为

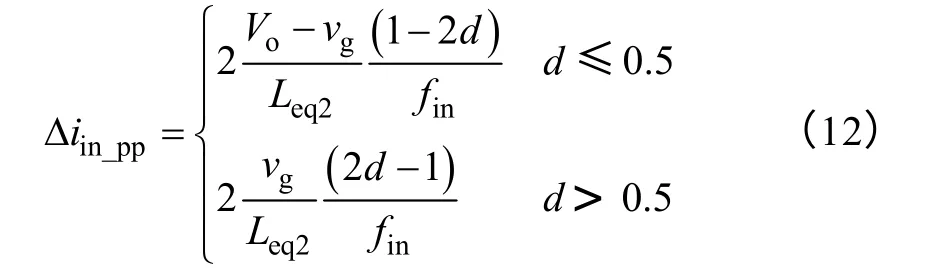
结合占空比表达式（2）、Leq2的表达式（3）和脉动频率的表达式（11），Δiin_pp关于占空比的表达式为

当给定输入输出电压和输入功率时，根据式（13）画出图5，从中可以看出：一定耦合系数时，由于交错并联对输入电流脉动的抵消作用，越靠近d=0.5的输入电流脉动越小；在同一占空比下，相应的输入电流脉动随着耦合系数的增大而增大。

虽然耦合可以降低电感的匝数，但增加了输入电流脉动的幅值，综合考虑电感匝数的降低和耦合电感的制作难度，后文分析计算中的电感耦合系数α=1/3[9]，取Vo=390V，Pin=300W，Lcp=360μH。图6给出了输入电压为110V 和220V 时，半个工频周期内fin和Δiin_pp的变化曲线。由于电感耦合，fin在d=0.5附近降低，在输入电压过零处，d接近1，fin增加。输入电流脉动幅值在输入电压过零处开始，随占空比的降低逐渐增加，在接近d=0.5 时逐渐降低，并在d=0.5 时降为零，之后再随占空比的降低逐渐增加。同时，输入电流脉动的幅值因电感耦合而有所增加。

图6 半个工频周期内的占空比、输入电流脉动幅值和频率Fig.6 Magnitude and frequency of input current ripple in a half line cycle for non-coupled and coupled cases

3 输入差模EMI 频谱的计算

3.1 输入差模EMI 干扰值的计算

通过列写半个工频周期内输入电流的时域波形表达式，基于傅里叶变换计算其各次谐波的幅值，是不能作为输入EMI 干扰值的。为此，需要对EMI接收进行建模，通过计算相应频率的峰值干扰（Peak，PK）、平均值干扰（Average，AV）或准峰值干扰（Quasi-Peak，QP），得到特定条件下的EMI干扰频谱。下面将应用文献[11]给出的计算单路CRM Boost PFC 变换器EMI 干扰频谱的思路和接收机模型，对交错并联CRM Boost PFC 电路输入电流脉动进行EMI 干扰值的计算和频谱分析。

图7a 给出了包括线性阻抗网络（Line Impedances Stabilizing Network，LISN）、差模分离器和被测变换器拓扑的差模干扰测试示意图。在标准规定的测试频段[15]（150kHz～30MHz）内，其可简化为图7b，其中RLISN=50Ω。若变换器输入不加滤波器，LISN 输出的干扰电压值将超过实验中接收机的输入电压上限值。为此，本文在整流桥后放置了高频电容，Cx=0.47μF，用于适当滤除电感电流的高频分量，以降低 LISN的输出电压值。Cx较小时,仅会适当减小差模干扰电压幅值并给干扰频谱中引入−20dB/格斜率的衰减。

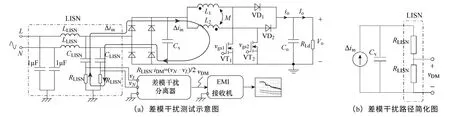
图7 考虑LISN 和干扰分离器的差模干扰路径Fig.7 DM noise loop considering LISNs and noise separator

由于输入电流中的高频脉动电流分量Δiin，是引起差模干扰的主要来源，且脉动电流频率极大于两倍工频，所以半个工频周期内的任意时刻都可以近似为一个脉动周期。由图2 可知，一个脉动周期内输入电流脉动可表达为式（14）。若以脉动电流频率fin为基频，以式（14）中的函数作为一个周期函数进行傅里叶分解，则对应频率为nfin的谐波幅值 |cn(d,nfin)|可表达为

谐波幅值正比于Δiin_pp且受d和谐波次数n的影响。图8 计算了不同谐波次数时式（15）中除Δiin_pp外含有d和n的项随占空比的变化曲线。其中，基波分量（n=1）的幅值大于其他谐波次数的值，且变化范围仅为[0.318,0.405]。所以可以认为占空比对基波的影响范围较小，电感电流脉动幅值Δiin_pp可以表征基波幅值|c1(d,fin)|的变化。且易得到谐波幅值随n的增加以−40dB·μV/格或−20dB·μV/格的斜率衰减。

图8 n 和d 对谐波幅值的影响Fig.8 Effects of n and d on the magnitude of harmonics

LISN 输出的信号为脉动电流各次谐波在50Ω电阻上产生的电压信号。将电压信号送给EMI 接收机，根据接收机模型对信号进行处理，可得到相应的干扰值。对于变频模式的CRM Boost PFC 变换器，由于QP 值与AV 值的差值总是大于10dB·μV，因此在设计滤波器时应该更加关注QP 值[11]。而QP值的计算较复杂[11]，且变频控制时干扰的QP 值与PK 值比较接近。所以本文是以差模干扰PK 值作为被测频率的EMI 干扰值，分别计算150kHz～1MHz范围内一定数量的差模干扰PK 值，来得到EMI 干扰频谱。

3.2 输入差模EMI的频谱计算和分析

分别取输入电压为85V 和265V，Vo=390V，Lcp=360μH，计算耦合前后不同输入功率下的差模EMI 干扰频谱，如图9 所示。给定Vin，随着Pin的增加，开关频率减小，变换器的干扰频谱整体向频 谱图的低频段移动。同时，由于电感电流脉动幅值的增加，干扰频谱幅值整体上升。由于输入脉动电流谐波幅值有−40dB·μV/格或−20dB·μV/格的衰减，而Cx又引入了−20dB·μV/格的衰减，最终的EMI 干扰频谱的渐近线呈现了近似−60dB·μV/格或−40dB·μV/格的衰减（下面的测试也表明了计算的准确性）。

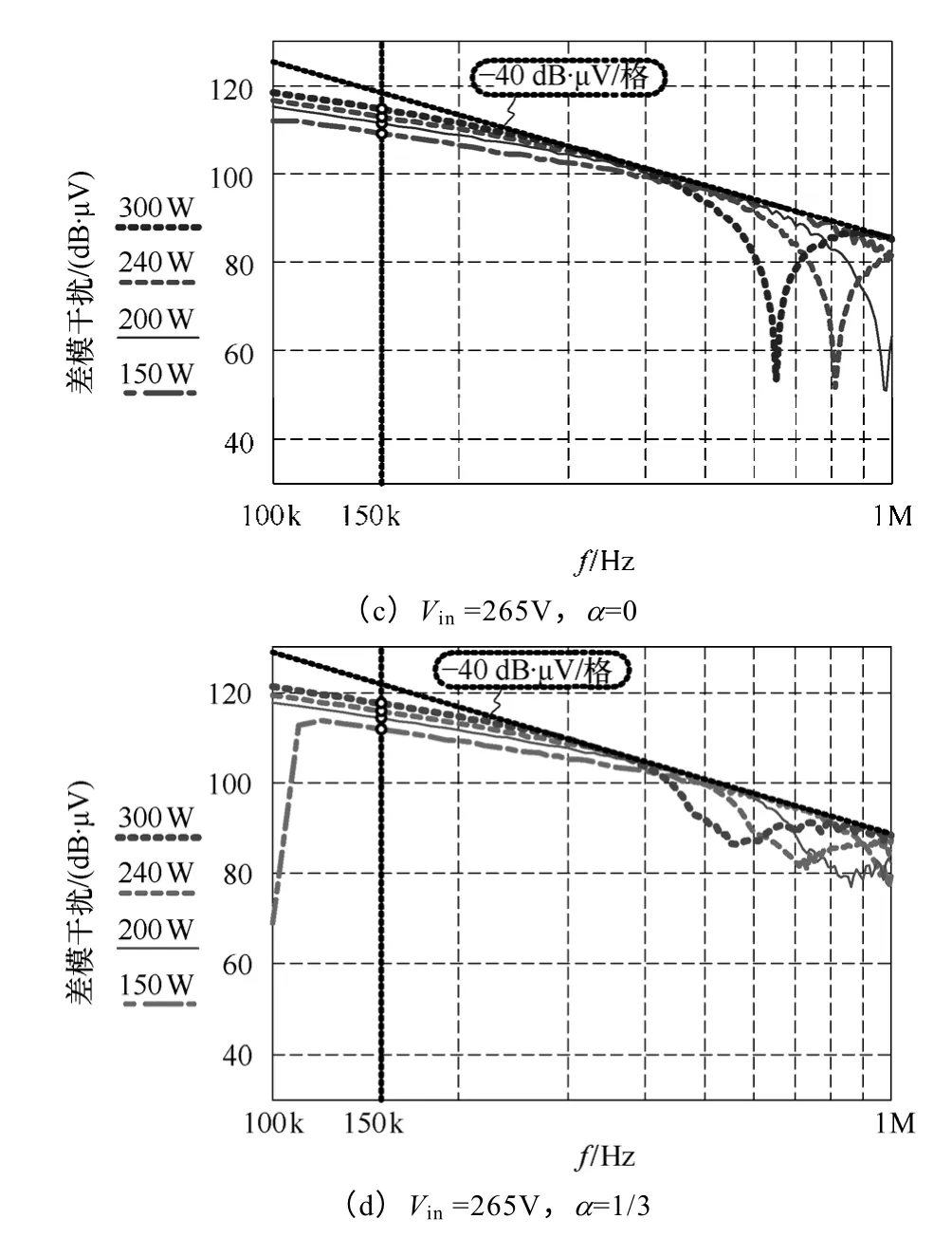
图9 电感非耦合时不同输入功率下的差模干扰频谱Fig.9 Calculated DM noise spectrums of non-coupled case in different input powers

EN55022 Class B 中针对传导电磁干扰在150kHz～30MHz 频率范围内定义了限制[15]。同时，EMI 滤波器的设计需要保证变换器的干扰在任何输入电压或负载情况下都满足标准的要求，因此需要找到干扰频谱的最恶劣情况，根据最恶劣频谱中关键频率fcrit的干扰值设计滤波器的转折频率[10]。由于变换器工作在变频模式，如图9 所示，干扰频谱较为连续，且频谱幅值随频率的增高呈现一定衰减。滤波器的转折频率基本是由150kHz的干扰值决定的，可以认为150kHz 是fcrit。那么最恶劣干扰频谱就是150kHz的干扰出现最大值时的频谱，所以下面将针对150kHz的差模干扰值作讨论，分析其出现最大值的条件。

fin在半个工频周期内是变化的（见图4），其最低值fin_min出现在瞬时输入电压峰值处（d=1-），且随输入功率的增加而降低。取Vo=390V、Lcp=360μH，由式（11），耦合前后不同输入功率时fin_min随输入电压的变化曲线如图10 所示。由于EMI 标准更关心150kHz 及更高频率的干扰值，依据额定输入功率Pin=300W 时的fin_min曲线和150kHz的关系，可以将输入电压分为三种情况：当85V≤Vin＜118V 时(电 感 耦 合 时，85V≤Vin＜146V），一定输入功率时出现150kHz的脉动；当118V≤Vin＜238V 时(电感耦合时，146V≤Vin＜239V），全负载范围内，输入电流脉动频率都大于150kHz，即不存在150kHz的电流脉动；当236V≤Vin＜265V（电感耦合时，239V≤Vin＜265V），在一定输入功率出现150kHz的脉动。因此以下的计算主要在85V 和265V 电压附近。

图10 最低输入电流脉动频率随输入电压的变化曲线Fig.10 Minimum input current ripple frequency varied with input voltage

4 150kHz的电流脉动幅值分析

前文分析指出，输入电流脉动的基波变化趋势与其脉动电流幅值类似，而PK 值基本是由对应频率脉动电流的基波决定的。所以，可以利用脉动电流幅值的变化规律来预测出现最大干扰PK 值的条件。

将式（2）带入式（11）和式（13），可得耦合前后一定输入电压下，半个工频周期内输入电流脉动幅值和频率随输入功率变化的曲线，如图11 所示。随着输入功率的增加：在85V 时，150kHz的输入电流脉动先增大后减小，脉动最大值并不出现在满载处；在265V 时，150kHz的输入电流脉动值逐渐增大。可见，150kHz的输入电流脉动由输入电压和输入功率共同决定。电感耦合也有类似结论，如图11c 和图11d 所示。

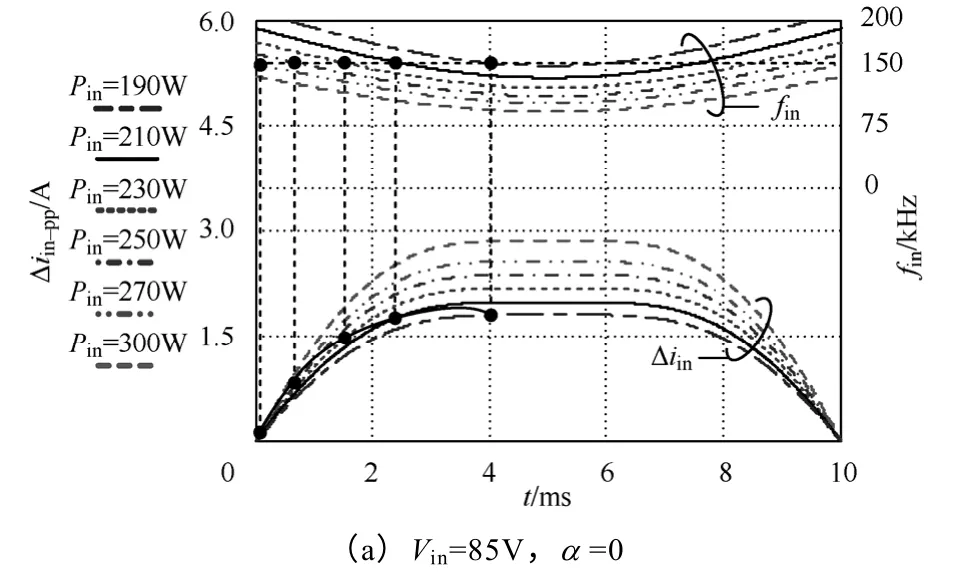
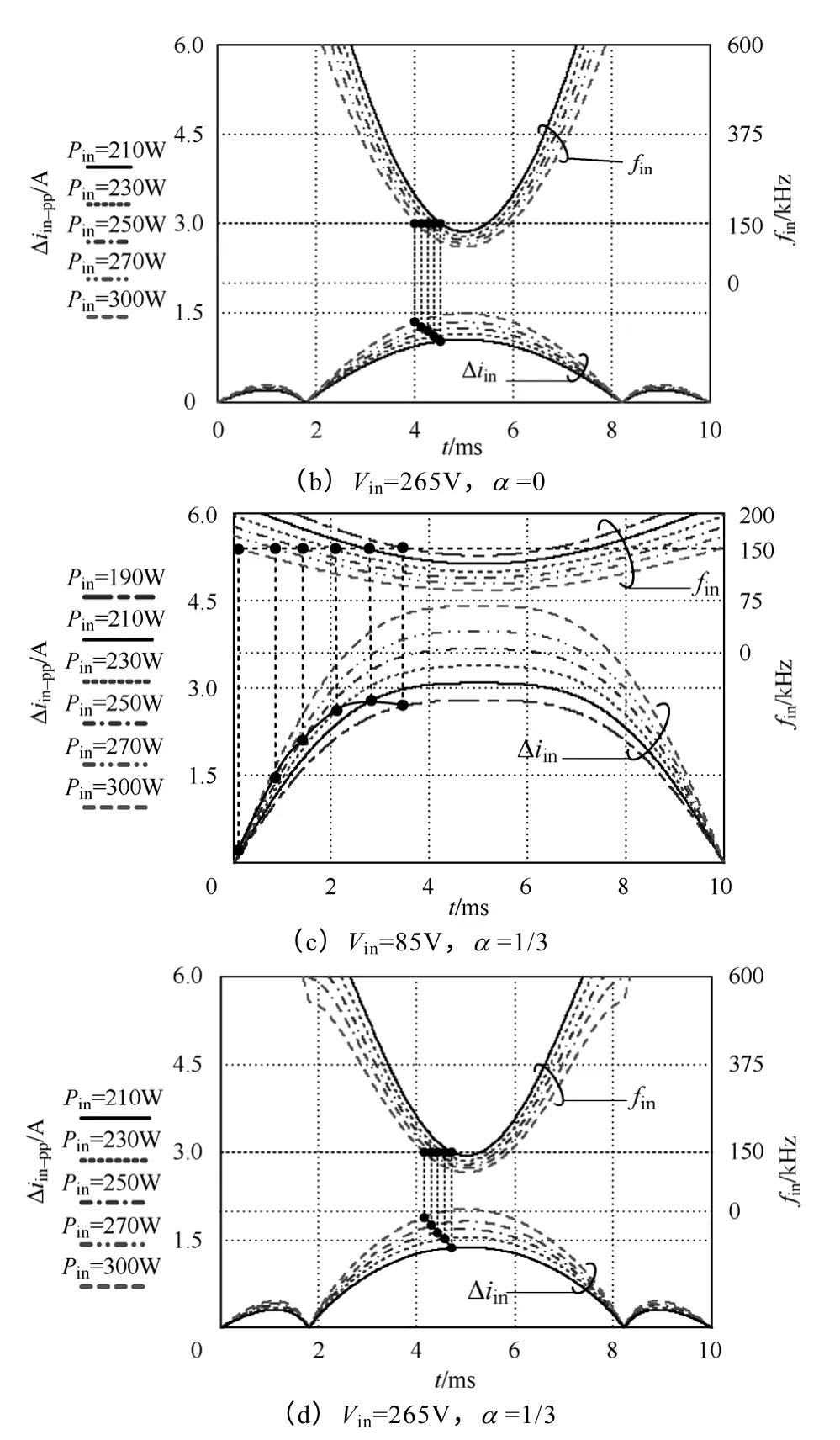
图11 耦合前后半个工频周期内的输入电流脉动幅值和频率Fig.11 Calculated input current ripple and frequency in a half line cycle varied with input power

若定义输入电流脉动频率为fcrit时的占空比为dfcrit，由式（12），则其对应的电流脉动表达式为

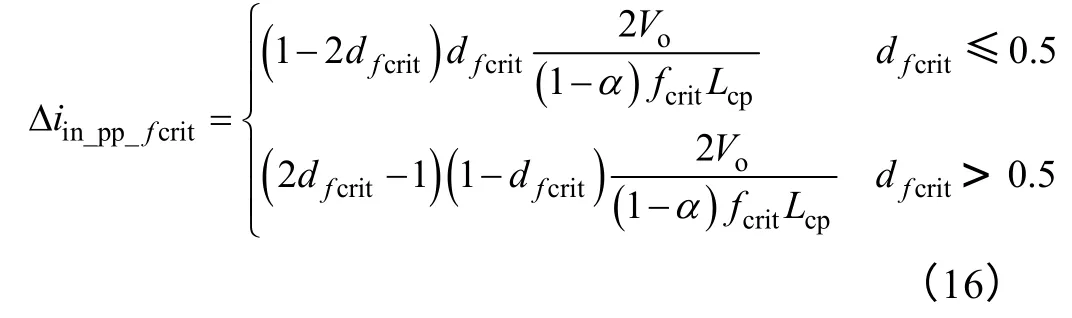
显然，当dfcrit=0.25（dfcrit≤0.5）或dfcrit=0.75（dfcrit＞0.5）时，式（16）取到最大值。

最大值只与输出电压，耦合系数和自感值有关，且随着耦合系数的增加而增加。

由式（13），分别取dfcrit等于0.25 和0.75，推得频率为fcrit的电感电流脉动幅值出现最大值时对应的输入功率为

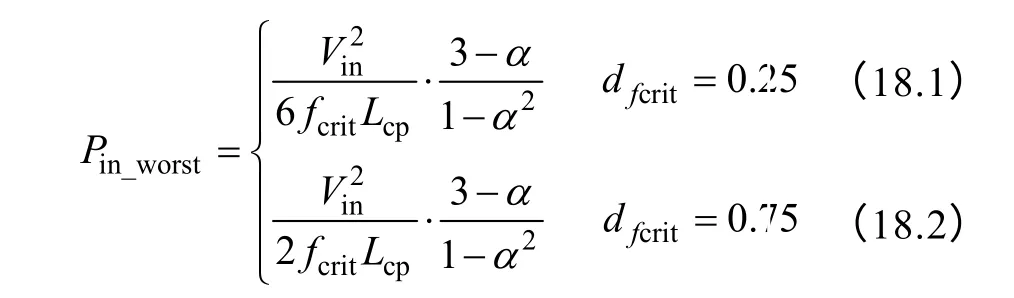
通过MathCAD 解出式（11）中dfcrit随输入功率Pin变化的表达式（19）。由于给定输入输出电压时，半个工频周期内的占空比有一定的变化范围，当Pin从零变化到额定输入功率，式（19）计算出的占空比并不是都有意义。所以，最终频率为fcrit输入电流脉动随输入功率的表达式为式（20）。

将式（19）带入式（20），取fcrit=150kHz，Vo=390V，L=360μH，在不同输入电压下，可得耦合前后150kHz 输入电流脉动幅值随着输入功率变化的曲线，如图12 所示。当不存在150kHz的频率时，电流脉动幅值为零。电感不耦合时如图12a 所示，当85V≤Vin≤118V 时，存在150kHz的干扰值，若式（18.2）算得的功率低于额定功率，即Pin_worst≤Pin_reated，可推得（本文 中，如 85V、95V 和104V，电流脉动幅值随着Pin的增加先增加后降低，分别在由式（18.2）计算得到功率，200W、250W 和300W 达到最大值(黑色圆圈)；当如110V，由于在[0W,300W]的输入功率范围内，150kHz的脉动电流达不到最大值，其仅随着输入功率的增加而增加；当118V＜Vin＜238V 时，在输入功率范围内所有脉动频率均大于150kHz（见图10），所以没有150kHz 脉动幅值；当 238V≤Vin≤265V 时，如240V、250V、260V 和265V，在输入功率范围内dfcrit都取不到0.25，脉动电流达不到最大值，仅随输入功率的增加而增加。以上规律适用于耦合电感和非耦合电感，只是电压区间略有区别，如图12b所示。同时，当α=0 和α=1/3 时，由式（18.2）可 得。

图12 耦合前后150kHz的输入电流脉动随 输入功率的变化曲线Fig.12 Input current ripple when fcrit=150kHz varied with input power

同样的，取Vo=390V，Lcp=360μH，fIF=150kHz，可以计算不同输入电压时，耦合前后150kHz的干扰PK 值随着输入功率变化的曲线如图13 所示。由图可见，其与图12 中的输入电流脉动变化规律类似，且干扰最大值与输入电流脉动最大值的功率基本相同。这是因为在150kHz的电感电流脉动幅值为最大值时，占空比为0.25 或0.75。由图8 看出，其对应基波幅值也达到最大值，所以对应的差模干扰PK 值也达到最大值，且不同电压下的最大值相同。此时的输入电压和输入功率就是出现最恶劣差模干扰频谱的条件。

图13 150kHz的差模干扰PK 值随输入功率的变化曲线Fig.13 DM noise when fcrit=150kHz varied with input power

选取三个输入电压85V、95V 和104V，分别计算耦合前后满足150kHz的输入电流脉动为最大值时的差模干扰频谱，如图14 所示。由图14 可见，最恶劣频谱在大于150kHz的频段内几乎重合，且150kHz的干扰值基本相同。那么，差模滤波器只需依据电压 范围内某个输入电压下的最恶劣频谱进行设计即可。相对于非耦合情况(118.16dB·μV)，耦合增加了150kHz 输入电流脉动幅值，其干扰值也有所增加(121.68dB·μV)。

图14 150kHz 输入电流脉动幅值为最大值时的差模频谱Fig.14 DM noise spectrum when the current ripple magnitude at fcrit=150 kHz reaches the highest value

5 实验验证

为了验证上文的分析，实验室制作了一台300W的交错并联CRM Boost PFC 变换器样机，图15 给出了样机实物照片和测试平台。

图15 样机和EMI 测试平台照片Fig.15 Photos of magnetic components and the prototype

（1）变换器输入输出参数。输入交流电压：vin=85～265V/50Hz；输出直流电压：Vo=390V；额定输出功率：Po=300W；最低开关频率：25kHz。

（2）样机主要器件参数。Boost 开关管：2SK3569（600V,10A）；Boost 二极管：MUR460（600V,4A）；非耦合电感：360μH，74 匝；耦合电感：352μH，63 匝，耦合系数1/3；控制IC：CM6561（Champion）。

图16 和图17 为电感耦合前后，不同输入电压下不同输入功率时的差模干扰频谱PK 值。在图16 中，输入电压为85V 时，150kHz 干扰最大值在150W时出现，随着输入功率的增加，150kHz的干扰值下降；在90V、100V 和110V 时，随着输入功率的增加，150kHz的干扰值先增加后降低，分别在170W、210W 和240W 处出现最大值；在120V 和220V 时，150kHz 干扰值随着功率的增加而增大，在300W 处出现最大值。电感耦合时的频谱如图17 所示。

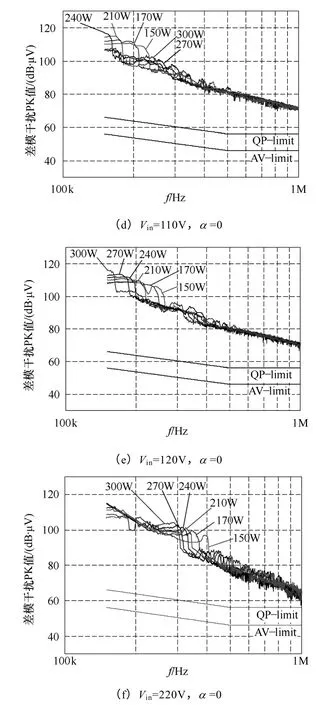
图16 电感非耦合时不同输入电压和输入功率下的差模干扰频谱Fig.16 Test results of the DM noise spectrums with non-coupled inductor

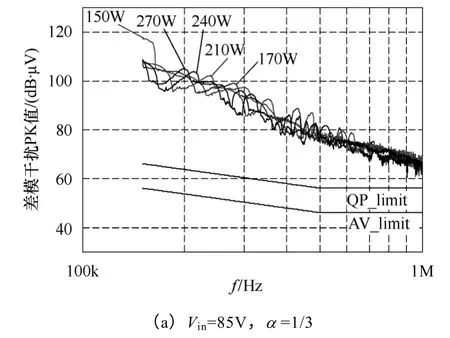
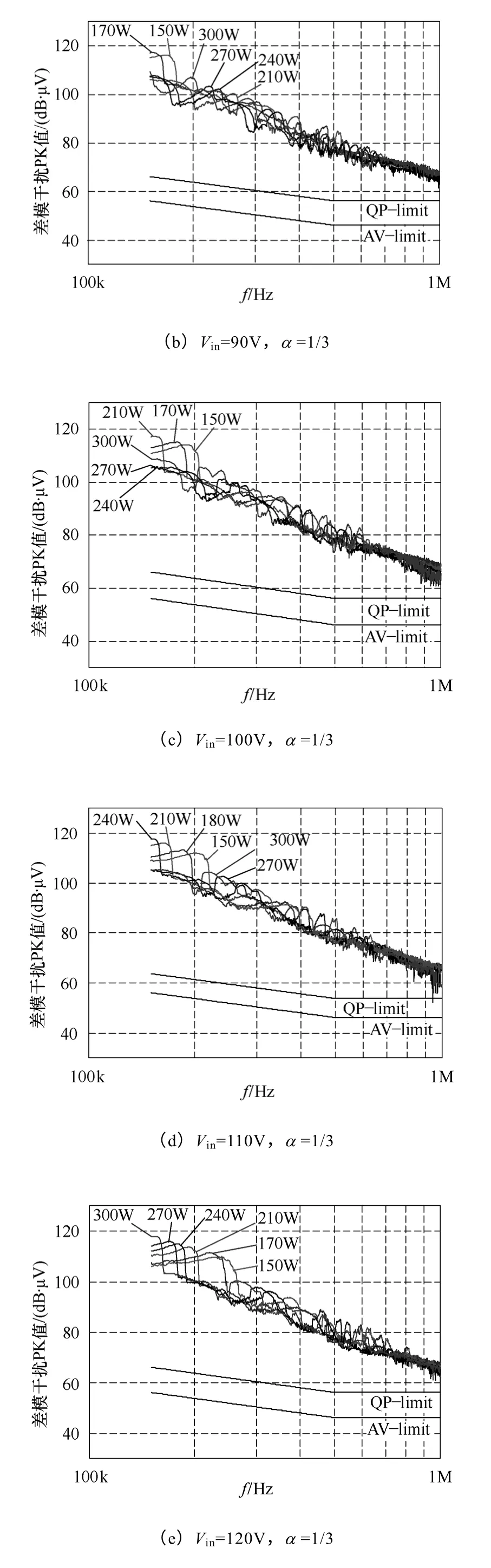
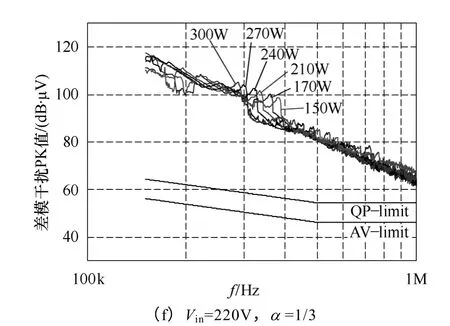
图17 电感耦合时不同输入电压和输入功率下的差模干扰频谱Fig.17 Test results of the DM noise spectrums with coupled inductor

由图16 和图17 中测得的频谱中150kHz的干扰值，绘出不同输入电压下，150kHz 差模干扰峰值随输入功率变化的曲线，如图18 所示（其中的数据点由直线连接）。由图可见，实验数据显示的变化规律与图13 中的计算结果较吻合。由于实验条件与计算参数并不能完全相同，且测量的数据有限，所以不同电压下实验得到的最恶劣输入功率与计算得到的并不是完全相同。但是由于150kHz的最大的电流脉动幅值与输入电压和输入功率无关，所以最大的差模干扰值仍基本相同的。电感非耦合时最大的差模干扰PK 值分别为115.83dB·μV（85V,150W）、116.12dB·μV（90V,180W）、115.7dB·μV（100V,210W）、115.63dB·μV（110V,240W）和115.57（120V,300W）；电感耦合时最大的差模干扰PK 值分别为117.18dB·μV（85V,150W）、117.03dB·μV（90V,180W）、116.95dB·μV（100V,210W）、117.01dB·μV（110V,240W）和117.83（120V,300W）。前文计算的耦合前后 150kHz 差模干扰 PK 峰值最大值为118.16dB·μV（α=0）和121.68dB·μV（α=1/3），其与实验值较接近。所以可以通过计算直接得到特定频率的差模干扰峰值最大值，进行滤波器设计。

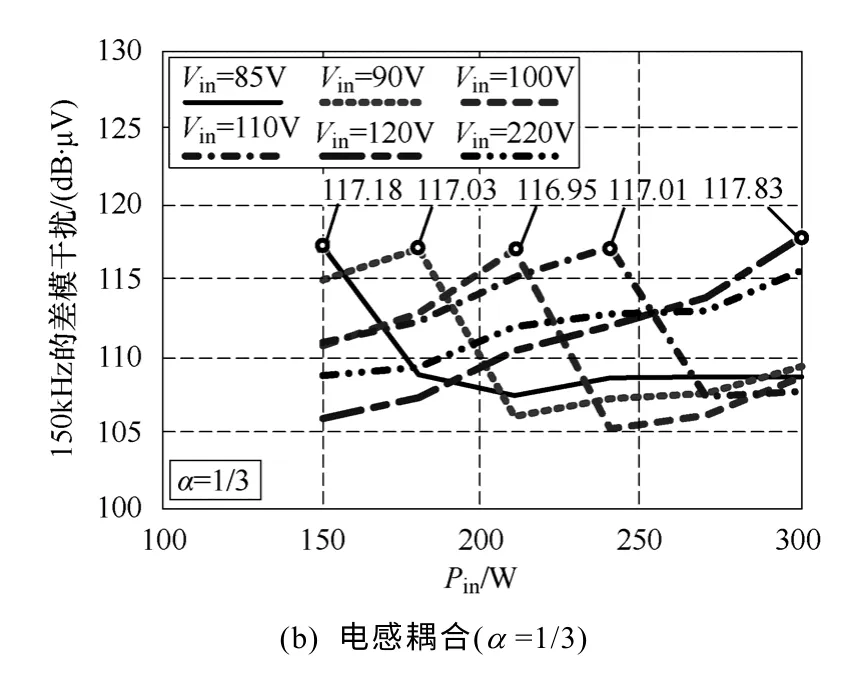
图18 不同输入电压时150kHz的干扰值随 输入功率的变化曲线Fig.18 Test results of the DM noise spectrums with coupled inductor

将耦合前后150kHz 干扰为最大值时的PK 值频谱和对应的QP 值频谱放在一起，如图19 所示。类似图 14，干扰频谱图几乎重合，且不同条件下的150kHz的QP 值基本相同。所以只要选取85V≤电压范围内的某一输入电压，找到其最恶劣的差模干扰频谱来设计滤波器即可，其他条件下的测试可以省去。

图19 电感耦合前后的最恶劣频谱Fig.19 Test results of the DM noise spectrums at the worst cases

分别选取耦合和非耦合两种情况下的一个最恶劣频谱情况进行比较，如图20 所示。耦合时150kHz的QP 值比非耦合时增加约3dB·μV，则EMI 滤波器的转折频率降低，若滤波电容值不变，则滤波电感值增加[16]。

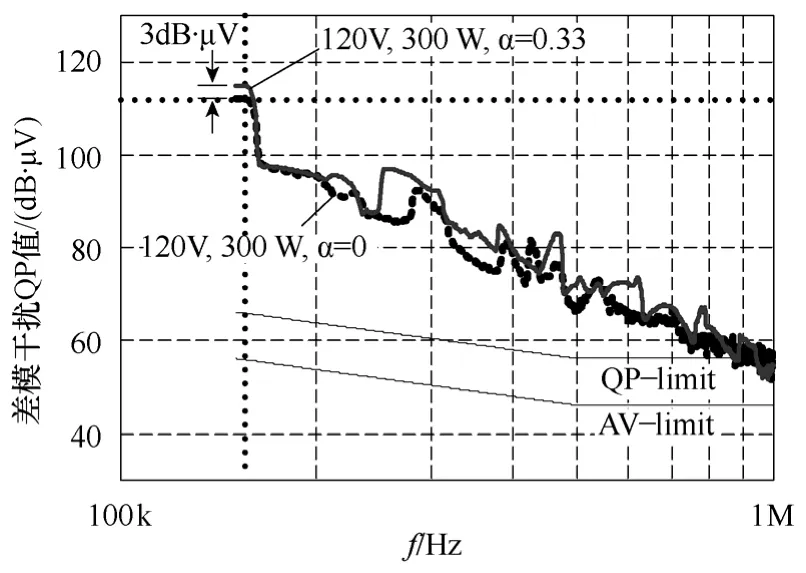
图20 电感耦合前后输入电流最恶劣频谱比较Fig.20 Comparison of the DM noise spectrums between coupled and non-coupled cases

6 结论

电流临界连续模式的交错并联Boost PFC 变换器的电感耦合后，开关频率发生变化，输入电流的脉动增加。但最恶劣频谱基本是150kHz的干扰值为最大值时的频谱。由于输入电流脉动和差模干扰峰值的对应关系，当150kHz的输入电流脉动出现最大值时，其对应的干扰值也为最大值。本文分析了不同电压下150kHz 频率的电流脉动随输入功率的变化情况，并给出了出现最大电流脉动幅值的输入电压范围和对应输入功率的计算方法，可用于指导实际测量和计算。

由于150kHz的输入电流脉动最大值在不同输入电压时相同，对应的最恶劣频谱中的150kHz的干扰值也相同，则只要找到某一电压时的最恶劣频谱，即可认为找到了宽输入电压范围和全负载范围内的最恶劣频谱。这样可以大大减少反复测量不同输入电压和功率时的差模干扰频谱，节省了时间和成本。

由于电感耦合导致150kHz 时的差模干扰值增加，差模电感值要适当增加。

[1]Elmore M S.Input current rippled cancellation in synchronized,parallel connected critically continuous boost converters[C].Proceedings of IEEE Applied Power Electronics Conference,1996:152-158.

[2]Ishii T,Mizutani Y.Power factor correction using interleaving technique for critical mode switching converters[C].Proceedings of IEEE Power Electronics Specialist Conference,1998:905-910.

[3]Noon J P.Designing high-power factor off-line power supplies[Z].Texas Instruments Power Supply Design Seminar,2003:1500.

[4]Wong P L,Xu P,Yang P,et al.Performance improvements of interleaving VRMs with coupling inductors[J].IEEE Transactions on Power Electronics,2001,16(4):499-507.

[5]Li J,Sullivan C R,Schultz A.Coupled inductor design optimization for fast-response low-voltage dc-dc converters[C].Proceedings of IEEE Applied Power Electronics Conference,2002:817-823.

[6]Zumel P,Garcia O,Cobos J A,et al.Magnetic integration for interleaved converters[C].Proceedings of IEEE Applied Power Electronics Conference,2003:1143-1149.

[7]Huber L,Irving B T,Adragna C,et al.Implementation of open-loop control for interleaved DCM/CCM boundary boost PFC converters[C].Proceedings of IEEE Applied Power Electronics Conference,2008:1010-1016.

[8]Wen W,Lee Y S.A two-channel interleave boost converter with reduced core loss and copper loss[C].Proceedings of IEEE Power Electronics Specialist Conference,2004:1003-1009.

[9]Yang Fei,Ruan Xinbo,Yang Yang ,et al.Design issues of interleaved critical conduction mode boost PFC converter with coupled inductor[C]Proceedings of IEEE Energy Conversion Congress and Exposition,2010:2245-2252.

[10]Shih F,Chen D Y,Wu Y,et al.A procedure for designing EMI filters for AC fine applications[J]IEEE Transactions on Power Electronics,1996,11(1):170-181.

[11]Wang Zijian,Wang Shuo,Kong Penju,et al.DM EMI noise prediction for constant on-time,critical mode power factor correction converters[J].IEEE Transactions on Power Electronics.2012,27(7):3150-3157.

[12]Nussbaumer T,Heldwein M L,Kolar J W.Differential mode input filter design for a three-phase buck-type PWM rectifier based on modeling of the EMC test receiver[J].IEEE Transactions on Industrial Electronics,2006,53(5):1649-1661.

[13]Giezendanner F,Biela J,Kolar J W,et al.EMI noise prediction for electronic ballasts[J].IEEE Transactions on Power Electronics,2010,25(8):2133-2141.

[14]Raggl K,Nussbaumer T,Kolar J W.Guideline for a simplified differential-mode EMI filter design[J].IEEE Transactions on Industrial Electronics,2010,57(3):1031-1040.

[15]EN55022:limits and methods of measurement of radio disturbance characteristics of information technology equipment[S].European,European Norm Standard,1994.

[16]Mainali K,Oruganti R,Viswanathan K,et al.A metric for evaluating the EMI spectra of power converter[J].IEEE Transactions on Power Electronics,2008,23(4):2075-2081.