基于连续小波变换的弱信号检测方法研究

马敬广马启明

（1.海军驻杭州地区军事代表室，杭州，310012）

（2.第七一五研究所 声纳技术重点实验室，杭州，310012）

基于连续小波变换的弱信号检测方法研究

马敬广1马启明2

（1.海军驻杭州地区军事代表室，杭州，310012）

（2.第七一五研究所 声纳技术重点实验室，杭州，310012）

在能够获得振动背景噪声和目标信号数据集的假设条件下，按照信噪比最大化准则，提出了一种基于连续小波变换（CWT）的弱信号检测方法，它首先设计一个能够使信噪比最大化的连续小波变换，用于对实际阵列输入信号的预处理；再将预处理结果用于MVDR波束形成，实现了对目标的检测和方位估计。实际数据分析结果表明，该方法能够提高在强振动噪声背景下的弱信号检测能力，其最小可检测信噪比较传统MVDR方法降低了7 dB。

声呐；弱信号检测；连续小波变换

当声呐部位自噪声以舰艇平台振动噪声、拖曳平台噪声干扰的近场辐射噪声成份为主时，其能量远大于远程目标，这使得声呐目标往往淹没在强背景噪声和强干扰中而成为微弱信号，仅利用常规处理很难探测到这样的远程弱目标。只有充分研究各种噪声、干扰和目标信号特性分布，甚至建立其模型的基础上，利用噪声、干扰和目标信号的一切可以利用的信息，才能提高抑制背景噪声并检测弱信号的能力。为此，我们假设可以通过实验或其它办法获得背景噪声和目标信号的一个有代表性的数据集。基于这一假设，国内外学者提出了多种微弱信号检测方法，其中“分类置前”思想最为典型，如D H Kil等人提出的全谱信号处理思想[1]，为声呐微弱信号检测提供了新的思路；Haykin等人将非平稳环境下的信号检测问题转化为自适应模式分类问题[2,3]；Richard等人通过魏格纳分布(WVD)将时域信号转化至时频联合域，通过特征提取和优化，利用训练好的模式分类器完成对弱信号的检测[4,5]。本文基于相同的假设（即能够获得背景噪声和目标信号的代表性数据集，并假设背景噪声和目标信号均是短时平稳的），以MVDR波束形成为基础，利用连续小波变换研究在强振动噪声干扰背景下的弱目标检测方法。

1 MVDR自适应波束形成的基本原理

目前，主要利用波束形成进行声呐目标检测与方位估计，其中常规波束形成(CBF)、最小方差无失真响应（MVDR）波束形成最为常用。与CBF相比，MVDR方法具有更高的空间分辨率和更强的干扰抑制能力等优点[6-8]，在强背景噪声和干扰条件下具有更好的应用前景。

MVDR的数学思想可用式(1)描述

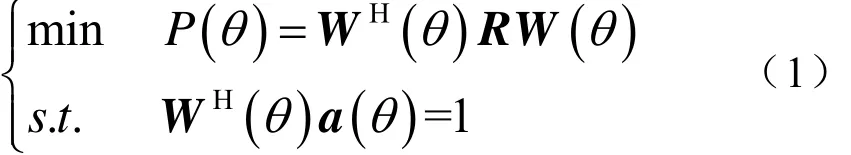
其中，P(θ)表示θ方向的阵列输出功率，W(θ)表示阵列权值，R表示阵列接收信号的协方差矩阵，a(θ)为方向驾驶向量，H表示共轭转置。利用拉格朗日乘子法可求得阵列空间能量谱：

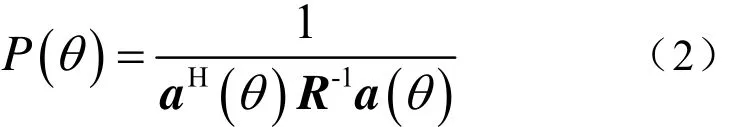
上式表示窄带阵列信号的空间能量谱的计算式，对于宽带MVDR，可利用频段分解方法[8]进行计算。

2 弱信号检测方法

尽可能的提高阵列输入信号的信噪比是提高系统弱信号检测能力的有效途径，但如何降低/抑制阵列输入信号中的噪声成分依然是水声信号处理研究领域的一个难题。国内外研究曾利用自适应噪声抵消技术或盲信号分离算法对阵列输入信号进行处理，以期提高信噪比。但由于这些方法的固有缺陷，如自适应噪声抵消的参考噪声不容易获得，盲信号分离模型难以建立等问题，使得这些方法对弱信号检测能力的提高非常有限。

我们的基本思路是：利用背景噪声和目标信号的代表性数据集，设计一种滤波器能够使阵列输入信噪比最大，进而提高系统对弱信号的检测能力。我们知道，对于确知信号的检测问题，匹配滤波（相关检测）是一种信噪比最大意义上的最优检测方法，但由于我们的目的并不是设计检测器去检测训练样本集内的指定目标信号，而是检测在统计特性上与训练样本集内目标信号相近的信号，这就会引起匹配滤波器的性能急剧下降。因此，需要设计其它的线性相位滤波器(FIR)。

我们将连续小波变换（CWT）引入信号处理，设计一定尺度的小波变换（等价于FIR滤波器的设计），能够使得训练样本集内的目标信号和背景噪声的信噪比最大。首先将训练样本集内的目标信号和背景噪声分别进行连续小波变换（CWT），使它们在某一尺度的信噪比最大；其次，对此尺度下的小波系数进行波束形成，实现对目标信号的检测和方位估计。由于小波变换与滤波器具有某种程度的等价性，这一处理过程与根据信噪比选择信号频段有些相似。但是，由于有更多的小波函数可供选择，而且还可以根据实际应用需要设计小波函数，滤波器带宽也可以通过调整尺度因子而设定，使得连续小波变换较带通滤波器组具有更大的灵活性。

设ψ(t)是基本小波，连续小波函数ψa,b(t)由下式定义[9,10]

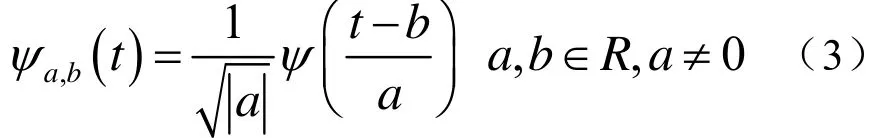
其中，a为尺度因子，b为平移因子，对于f(t)∈L2(R)，其连续小波变换定义为

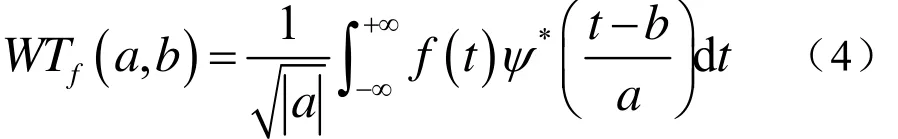
式中，*表示共轭。

从式（4）可以看出连续小波变换具有线性性和平移不变性，这就保证了原始信号和小波系数相位的一致性，从而使得我们利用原始信号在某一尺度的小波系数进行波束形成而不改变目标信号的方向特性。在本文的实际试验数据分析中，我们选用较为常用的“Sym8”小波函数分别对训练样本集内的目标信号和背景噪声进行连续小波变换，尺度变化范围根据声呐的工作频段选定，得到信噪比最大的尺度。在此尺度下，对实际阵列接收到的信号进行连续小波变换，并对小波系数做波束形成，进而完成目标信号的检测和方位角估计。

3 实际试验数据分析

利用小尺度舷侧阵声呐湖试数据验证本文方法的性能。目标信号选用实际舰船噪声，通过换能器发射；振动噪声通过激振器激励某小尺度模拟壳体来获得，并按照实际声呐平台噪声分布特性来调节激励信号源以保证模拟的逼真度。

利用基于连续小波变换的弱信号检测方法（简写CWT+MVDR）和传统MVDR方法对湖试数据进行分析。图1给出了在不同输入信噪比（−30 dB、−35 dB、−37 dB和−39 dB）条件下得到的空间能量谱图，其中的目标信号方位均为45º，强振动噪声干扰位于90º方位附近。图2给出了本文方法和传统MVDR方法的输出信噪比与阵列输入信噪比变化的关系曲线。

图1 本文算法与传统MVDR方法的性能比较

图2两种方法的输出信噪比与阵列输入信噪比的关系

从实际数据分析结果可以看出，在输入信噪比小于−30 dB的情况下，传统MVDR算法已经不能检测出目标信号的存在，而本文提出的CWT+MVDR方法依然能够稳定的检测目标信号，并正确估计目标方位。如果以阵列输出信噪比−3 dB作为检测门限，本文方法的最小可检测信噪比能够达到−37 dB，而传统MVDR的最小可检测信噪比只有−30 dB。因此，本文方法的最小可检信噪比较传统MVDR方法降低了7 dB，大幅度提高了对弱信号的检测能力，增加了探测距离。

4 结论

本文在能够获得振动背景噪声和目标信号代表性数据集的假设条件下，给出了一种基于连续小波变换的弱信号检测方法。实际数据分析表明，该方法在强振动噪声背景下的检测性能显著优于传统MVDR方法。但本文方法也有一定的局限性，即如何获得感兴趣的目标信号数据集。为了寻求解决方法，后续工作将建立目标信号模型，并研究利用目标信号模型替代目标数据集用于弱信号检测的可行性。

[1] SHIN F B, KIL D H. Full spectrum signal processing using a classify-before-detect paradigm[J]. JASA, 1996, 99(4):2188-2197.

[2] HAYKIN S, BHATTACHARYA T K. Modular learning strategy for signal detection in a nonstationary environment[J]. IEEE Trans. Signal Processing, 1997, 45(6):1619-1637.

[3] SIMON HAYKIN, DAVID J THOMSON. Signal detection in a nonstationary enviroment reformulated as an adaptive pattern classification problem[J]. Proceedings of IEEE, 1998, 86(11):2325-2344.

[4] CÉDRIC RICHARD, RÉGIS LENGELLÉ. Data-driven design and complexity control of time-frequency detectors[J]. Signal Processing, 1999,77:37-48.

[5] CÉDRIC RICHARD.Time-frequency-based detection using discrete-time discrete-frequency wigner distributions. IEEE Transactions on Signal Processing, 2002, 50(9): 2170-2176.

[6] SWINGLER D N. A low-complexity MVDR beamformer for use with short observation times[J]. IEEE Trans., Signal Processing, 1999, 47(4):1154-1160.

[7] CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proc. IEEE, 1969, 57(8):1408-1418

[8] 马启明. 强干扰下的宽带被动声呐的微弱信号检测理论和方法研究[D].浙江大学, 2008.

[9] MA QI-MING, WANG XUAN-YIN, DU SHUAN-PING. Method and application of wavelet shrinkage denoising based on genetic algorithm[J]. J Zhejiang Univ SCIENCE A, 2006, 7(3):369-375.

[10] MALLAT S G. 信号处理的小波导引[M].杨力华,译.北京: 机械工业出版社, 2002.