修正克隆遗传算法在分布式电源规划中的应用

李阳，周步祥，林楠，冯超，刘金华

（1.四川大学电气信息学院，成都 610065；2.四川电力职业技术学院，成都 610713；3.二滩水电开发有限责任公司，成都 610051）

修正克隆遗传算法在分布式电源规划中的应用

李阳1，周步祥1，林楠2，冯超1，刘金华3

（1.四川大学电气信息学院，成都 610065；2.四川电力职业技术学院，成都 610713；3.二滩水电开发有限责任公司，成都 610051）

在分析微电网中分布式电源特性的基础之上，构建了相关的目标函数与数学模型，提出一种针对微电网系统的修正克隆遗传算法。该算法在传统克隆遗传算法基础之上，加入修正表和局部搜索操作，提高了搜索效率，从而能更快速地获得微电网中分布式电源的最优化配置。最后在IEEE39节点算例上，应用此算法在计算机上进行仿真，结果表明了该算法的可行性和有效性。

微电网；分布式电源；修正克隆遗传算法；目标函数

随着社会与经济的飞速发展，世界各国对节能减排，更清洁、更高效、可再生的能源方面的研究日益增多[1-4]。太阳能电池、风力发电机、燃料电池、光伏电池等一系列小容量的分布式电源DG （distribution generation）以其高效率、能源种类多等独特的性能[5-8]，受到了电力行业广泛的关注。微电网是由各种负荷以及多种不同类型的分布式电源共同组成的系统，这些分布式电源由于时间和气候环境等因素的影响而具有很大的不确定性。因此，微电网系统也往往随之在不同的时间和环境下，具有不同发电特性或者用电特性。微电网中分布式电源的接入，提高了供电安全性、可靠性和经济性，保证了电能质量，实现了对用户提供可靠、经济、清洁、互动的电力供应和增值服务[9-12]。

文献[13]针对放射性配电网，采用数值算法，根据配电网网损和连续电流模型，确定DG的接入位置和容量。文献[14]提出了一种结合粒子群算法，来获得配电网中DG的最优化配置，该方法计算速度相对较快，除了可较好地增加电网负载率之外，还能很明显地改善电压电能质量。文献[15]采用一种蚁群算法来搜索最优的DG规划方案，但该算法必须调节出十分合理的各参数的比例，才能获得最优化结果。

本文提出的修正克隆遗传算法是在传统克隆遗传算法基础之上，提出的一种新的DG接入和最优化配置的算法，该算法不仅仅继承了传统克隆遗传算法仅在一条染色体上进行移位变异操作，不进行交叉操作导致出现“早熟”收敛现象的优点之外，同时还根据微电网和分布式电源的特点，加入了修正表和局部寻优操作，提高了算法运算效率。算例仿真表明，该算法用于微电网分布式电源的最优化配置的研究中，操作简单，收敛速度快，能较准确获得最优解。

1 微电网分布式电源模型的建立

首先建立含分布式电源的配电网规划模型，在满足相关的节点电压、电流约束条件的同时，最大程度上降低系统网损和分布式电源的总体投资费用，目标函数可由下式表示：

式（1）中ω1和ω2为加权因子，且ω1+ω2=1；Tmax为最大年负荷小时数；Cpu为单位电价。式（2）中Ui为节点电源幅值；PGi、QGi为节点i注入的有功功率、无功功率；Bij、Gij、αij分别为支路电纳、电导和节点i与节点j之间的相角差。式（3）中Umax和Umin分别为第i个节点的电压最大、最小幅值；Imax为支路上允许流过电流的最大值；PDGmax和PDGmin分别为DG有功出力的上下限。

2 修正克隆遗传算法

2.1 染色体编码

本文采用4位二进制进行编码，用变量X= （x1，x2，…，xn）来表示微电网中节点i的DG接入方案，从而进一步确定DG的位置和容量。若获得的值xi=0，则该节点不考虑DG的接入；若xi≠0，则该节点考虑安装DG，且容量Wi=xiw0，其中w0为额定容量，在此取为90 kVA。

2.2 种群的初始化

随机产生一个初始群体。首先，淘汰不符合以上两种规则的个体；然后对初始群体进行适应度计算，优选适应度排在前面的若干个体，重复几次后获得M个个体作为初始种群。

2.3 基因选择和变异操作

基因选择通常情况下是指进行复制、繁殖操作，在此采用适应度比例法进行优秀个体的选择操作，获得适应度较高的个体。若设置种群规模为M，个体适应度为si，则个体i被选中的概率为

基因变异操作是模拟生物进化过程中，由于某些偶然因素而引发的突变现象。就是指按照一定的变异率pm，随机选取个体染色体的某个位置的基因进行改变。当采用二进制编码时，变异操作就是实现某基因位置“0”和“1”翻转操作。

2.4 适应度函数的确定

在遗传算法中，通常用适应度函数来评价染色体个体的优劣，其中每一个个体被遗传到下一代的概率，是由该个体的适应度函数来确定，适应度函数是指导算法搜索方向的依据。而适应度函数要求优化问题为求最大值，且为非负值。因此，需要将目标函数与适应度函数进行一定的转化。

邢双双等[8]认为护理质量评价指标体系应覆盖临床常见病和多发病，应利于临床专科使用，应明确各个指标的界定标准。本研究指标体系包括15项安全及消毒隔离敏感指标，9项护理记录及评估敏感指标，12项医嘱执行及服务流程敏感指标，3项输血专项敏感指标，内容涵盖护理质量过程和结局，适宜各类病人使用及临床各护理单元的护理质量管理。

在本文分布式电源优化配置问题中，适应度函数为系统网损耗费和投资费用加权和所得到的目标函数F（x）通过相关变形而获得。即若设K为任意充分大的实数，则建立非线性加速适应度函数Fitness（x）为：

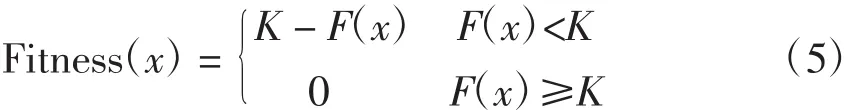
2.5 修正表

本文采用修正克隆遗传算法，引入修正表对算法进行修正，避免算法多次重复地计算，提高算法的速度。

首先，在进行DG优化配置过程中，若将DG配置在系统末端时，流过线路的有功和无功都将会减少；而若将DG配置在系统变电节点上，则往往只能改变电源总的容量，却不能提高线路最终的负载能力的大小。因此，在进行分布式电源最优化配置的时候，需将属于这两种情况的配置方案植入修正表，进行修正。其次，需把已经搜索到并进行了潮流计算得出适应度的点所对应的染色体及其适应度加入修正表中，赋予其修正属性。再以后产生的染色体都先用修正表来判断其属性，如果不在修正范围之内，则可以进一步判断潮流约束条件和计算其适应度值。如果属于修正范围中，则直接加入修正表，不进行重复计算。

2.6 优选操作和局部搜索操作

为了加快计算速度，保证每个子代都能优于下一代个体，采用局部优选操作。当经过遗传操作之后产生的新的个体优于当前个体，则执行优选操作，直接将当前个体予以淘汰，用新产生的个体进行替换；若产生的新个体劣于当前个体，则进行局部寻优操作，这样不仅仅大大加快了寻优的速度，同时也保证了子代的优越性。

2.7 终止条件

当满足以下两条件时，达到遗传终止条件：

1）值之差在某一个任意小的正数φ所确定的范围中，可表示为

其中：Snew为种群中新一代中最优的个体适应度值；Sold为种群中前一代中最优的个体适应度值。

2）达到最大的遗传终止代数T。

2.8 计算流程图

综上所述，最终得出该算法的流程图如图1所示。

图1 修正克隆遗传算法的流程图Fig.1Flow chart of the improved CGA

3 仿真结果及算例分析

通过建立上述模型，下面在Matlab计算机环境下对IEEE39节点配电网系统进行分析。

如图2中所示的网架结构：其系统电压等级为35 kV，分布式电源节点安装比例不超过系统总容量的30%。在此取初始种群大小为90，交叉率取为0.5，变异率取为0.3，最大的遗传终止代数为60。

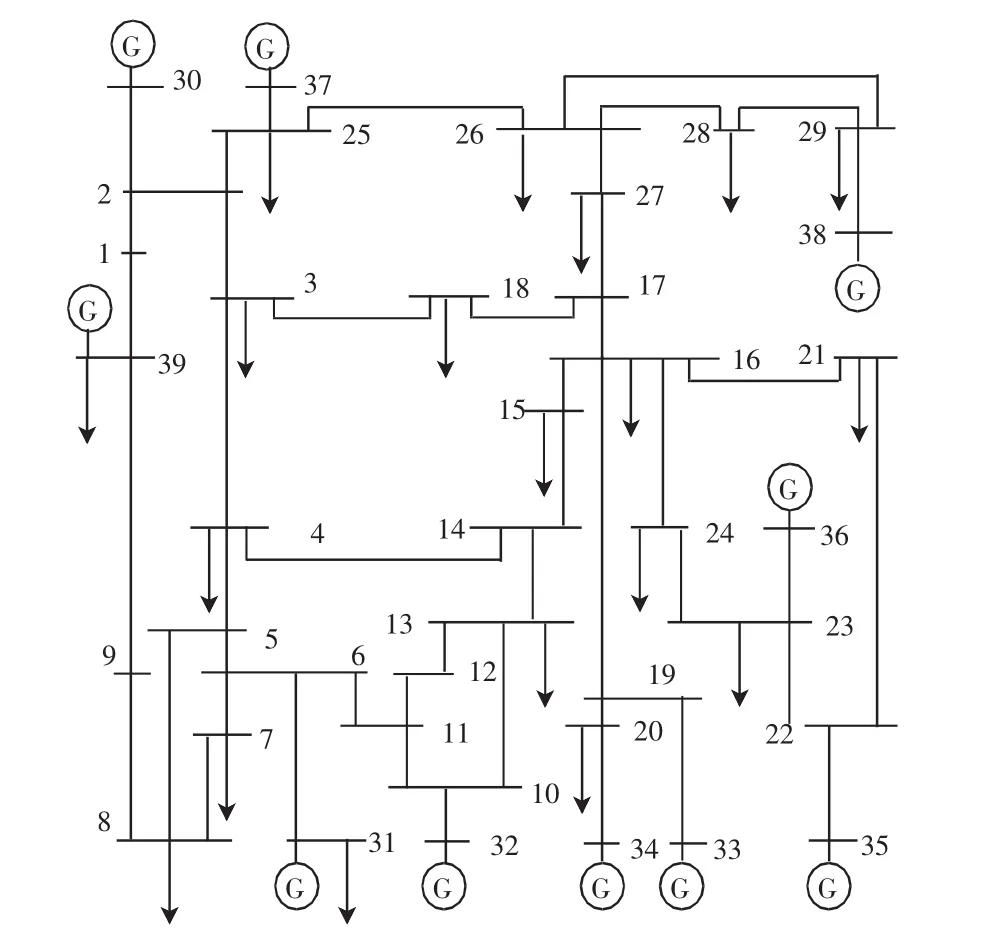
图2 IEEE39节点配电网系统接线图Fig.2IEEE 39-bus radial distribution system

下面对在不同权重系数之下，获得的目标函数的结果进行分析和对比。

其中权重方案I主要是考虑在欠发达地区，网损在配电网系统中所占比例相对较大，而分布式电源投入资金有限，取ω1=0.6，ω2=0.4时目标函数的结果。从表1的结果中可以看出，采用本文算法，在安装DG之前系统网损是275.087 kW，而当DG接入后网损为169.743 kW，有功网损下降率达到38.29%，

其中权重方案II主要是考虑在中等发达地区，配电网系统中线损率和分布式电源配置成本同样重要性，取ω1=0.5，ω2=0.5时目标函数的结果。从表1的结果中可以看出，采用本文算法，在安装DG之前系统网损是275.087 kW，DG接入后系统网损为188.602 kW，有功网损下降率达到31.44%。

其中权重方案Ⅲ主要是在比较发达地区，考虑网损在配电网系统中所占比例相对较小，分布式电源投入资金相对充足时，取ω1=0.4，ω2=0.6时目标函数的结果。从表1的结果可以看出，采用本文算法，在安装DG之前系统网损是275.087kW， DG接入后网损为216.897 kW，有功网损下降率达到21.15%。

表1 不同权重系数下IEEE39节点配电系统测试仿真结果Tab.1The results of different approaches for 39-bus distribution test system in different weight coefficients

同时，在图3给出了分别采用遗传算法和本文算法，所获得的IEEE39节点配电网系统进行优化的收敛曲线，从图3中可以看出，本文采用修正的克隆遗传算法计算效率更高，运算速度更快，有更好的收敛性。

图3 IEEE 39节点系统GA和CGA得到的优化收敛曲线图Flg.3Convergence curves of IEEE 39 bus system by GA and CAG

4 结论

本文采用修正克隆遗传算法来解决微电网中分布式电源的优化配置问题。采用该方法后能明显的降低系统网损、提高供电可靠率，该算法通过修正表和局部搜索的加入，有效提高了传统修正克隆遗传算法的计算效率。最后通过IEEE39节点测试系统，在计算机上进行仿真测试，表明了该算法的可行性和高效性。

由于各方面条件所限，本文没有考虑一些自然经济条件、以及相关国家政策对运行成本、维护成本、天然气以及其它发电和购电成本等对DG接入微电网的影响，有待进一步的研究与探讨。

[1]Kuri B，Li F．Distributed generation planning in the deregulated electricity supply industry[C]//IEEE Power Engineering Society General Meeting，Denver，USA：2004．

[2]钱科军，袁越（Qian Kejun，Yuan Yue）.分布式发电技术及其对电力系统的影响（Distributed generation technology and its impact on power systems）[J].继电器（Relay），2007，35（13）：25-29.

[3]余贻鑫，栾文鹏（Yu Yixin，Luan Wenpeng）.智能电网（Smart grid）[J].电网与清洁能源（Power System and Clean Energy），2009，25（1）：7-11.

[4]Hammons T J.Integrating renewable energy sources into European grids[J].International Journal of Electrical Power and Energy Systems，2008，30（8）：462-475．

[5]李兴源，魏巍，王渝红，等（Li Xingyuan，Wei wei，Wang Yuhong，et al）.坚强智能电网发展技术的研究（Study on the development and technology of strong smart grid）[J]．继电器（Relay），2009，37（17）：1-7．

[6]温阳东，王欣（Wen Yangdong，Wang xin）.分布式发电对配电网继电保护的影响（Effect of distributed generation on protection in distribution system）[J]．继电器（Relay），2008，36（1）：12-14，26．

[7]Dugan R C，McDermott T E，Ball G J.Planning for distributed generation[J].EEE Industry Applications Magazine，2001，7（2）：80-88．

[8]孙鸣，赵月灵，王磊（Sun Ming，Zhao Yueling，Wang Lei）. DG容量及接入方式对变电站继电保护定值的影响（Impart of DG capacity and location on relay protection of substation）[J]．电力自动化设备（Electric Power Automation Equipment），2009，29（9）：46-49．

[9]胡学浩（Hu Xuehao）.智能电网——未来电网的发展态势（Smart grid——a development trend of future powergrid）[J].电网技术（Power System Technology），2009，33 （14）：1-5.

[10]梁才浩，段献忠（Liang Caihao，Duan Xianzhong）.分布式发电及其对电力系统的影响（Distributed generation and its impaction on power system）[J]．电力系统自动化（Automation of Electric Power Systems），2001，25（12）：53-56．

[11]胡骅，徐冲，吴汕，等（Hu Hua，Xu Chong，Wu Shan，et al）.影响用户侧分布式发电经济性因素分析（Analysis of factors influencing economy of customer-side distributed generation）[J]．电力自动化设备（Electric Power Automation Equipment），2008，28（5）：29-33．

[12]崔金兰，刘天琪（Cui Jinlan，Liu Tianqi）.分布式发电技术及其并网问题研究综述（Distributed generation and its grid interconnection issue）[J].现代电力（Modern Electric Power），2007，24（3）：53-57.

[13]Coello C A C，Pulido G T，Lechuga M S．Handling multiple objectives with particle swarm optimization[J].IEEE Trans on Evolutionary Computation，2004，8（3）：256-279．

[14]Sheidaei Farnaz，Shadkam Majid，Zarei Mahdi．Optimal distributed generation allocation in distribution systems employing ant colony to reduce losses[C]//Universities Power Engineering Conference，Padova，Italy：2008．

[15]Ajay-D-Vimal Raj P，Senthilkumar S，Raja J，et al.Optimization of distributed generation capacity for line loss reduction and voltage profile improvement using PSO[J]. Elektrika，2008，10（2）：41-48．

Application of Improved Clonal Genetic Algorithm in Distributed Generation Planning

LI Yang1，ZHOU Bu-xiang1，LIN Nan2，FENG Chao1，LIU Jin-hua3
（1.School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，China；2.Sichuan Electric Power College，Chengdu 610713，China；3.Ertan Hydropower Development Company，Ltd.，Chengdu 610051，China）

Based on detailed analysis of the distributed generations′（DG）characteristics in microgrid，the objective function and mathematical model are built，and then the improved Clonal Genetic Algorithm（CGA）is proposed.Correctional operate and partial search are added to CGA in order to improve the search efficiency.Therefore，the optimal configuration of DG in microgrid is more rapid to obtain.Finally，the method is applied in IEEE 39 bus system.And compared with the other algorithm，the simulation results show that the algorithm is more feasible and effective.

microgrid；distributed generation（DG）；clonal genetic algorithm（CGA）；objective function

TM715

A

1003-8930（2013）04-0128-05

李阳（1987—），男，硕士研究生，研究方向为电力系统自动化及计算机信息处理、分布式电源等。Email：liyang2010vip@163.com

2011-07-05；

2011-08-09

周步祥（1965—），男，博士，教授，研究方向为电力系统自动化、计算机应用等。Email：hiway_scu@126.com

林楠（1973—），女，硕士，讲师，研究方向为电力系统自动化、计算机应用。Email：cdlinlan@yahoo.com