基于粒子群算法优化支持向量机的铁路客运量预测模型

朱伟，李楠，石超峰

(重庆交通大学 交通运输学院，重庆 400074)

0 引 言

随着社会经济的发展，铁路运输事业取得了长足的进步.作为衡量铁路运输发展的一个重要指标，铁路客运量预测一直占有重要的作用.而科学准确地预测铁路客运量及其仿真趋势、特点和规律是制定公路客运发展规划及规划铁路客运场站的重要理论依据［1］.传统的预测方法有时间序列预测法、弹性系数法、灰色系统预测等等［2］.近几年来，随着神经网络技术的发展，神经网络开始被应用到公路客运量预测中，它对解决非线性问题具有很好的效果，但是也存在着收敛速度慢、过学习和局部极值等问题［3］，在一定程度上影响了其准确性.

支持向量机是(Support Vector Machine，SVM)是基于Vapnik 提出的小样本学习理论建立的，着重研究小样本条件下的统计学习规律［4－5］.它克服了神经网络的一些固有缺陷，在小样本预测领域有着很好的应用效果［6］.但是支持向量机的预测精度与其参数的选择有很大的关系，参数选择的好坏对预测结果的影响很大.本文将粒子群算法和支持向量机结合，构建了基于粒子群算法优化支持向量机的铁路客运量预测模型.仿真实验结果表明，该模型预测精度更高，为铁路客运量预测提供了一种新的途径.

1 支持向量机的基本原理

支持向量机理论可用于分类问题和回归问题.其基本原理是通过一个非线性映射ø(x)，把输入数据x 映射到一个高维的空间，从而将非线性回归问题转化为高维特征空间的线性问题，即

其中，ø(x)是将样本点映射到高维空间的非线性变换;ωT为权值矢量;b 为阈值.

定义ε 不敏感损失函数为:

其中f(x)为回归函数求得的预测值，y 为相应的真实值，ε 为不敏感损失系数，即表示预测值与真实值之差小于等于ε 时，代表损失为0.

通过最小泛函分析得:

其中第一项称为模型复杂性项，第二项是由ε 不敏感损失函数确定的经验误差项，C 为惩罚系数.

引入K(xi，xj)核函数，把(4)转化为对偶形式来求:

2 PSO－SVM 预测模型的建立

惩罚参数C、RBF核参数σ、不敏感损失参数是决定支持向量机预测性能的三个重要参数.利用智能优化算法对支持向量机的参数进行优化选择，对提高其预测性能具有重要的意义.

粒子群算法是继蜂群算法，蚁群算法之外的一种群体智能算法，它是由Kennedy 和Bernhard 在1995年提出的，其基本思想源于对鸟类捕食行为的研究.利用PSO 算法求解最优化问题时，每一个粒子代表问题的一个解，并且每一个粒子都对应着一个适应度值，此适应度值主要通过适应度函数得到.粒子移动的方向和距离由粒子的速度决定，而速度通过自身及其身边的粒子的移动经验进行动态更新，从而实现对解的搜索.在每一次寻优过程中，粒子通过两个“极值”来更新自己，一个是个体极值Pbest(粒子本身搜索得到的最优解)，另一个是群体极值Gbest(全局最优解).粒子群优化支持向量机参数的相关步骤如下:

(1)设置PSO 初始参数，如种群数、迭代数，变异率、交叉率等.随机产生一组粒子的初始位置和速度.

(2)选择适应度函数，本文选择均方误差作为适应度函数来判断参数选择的优劣.

(3)根据两个对比更新粒子的位置.当前适应度值和所经历过最好位置pbest 对比，若当前适应度好，则更换当前适应度值为最好位置;当前适应度值与全局最优位置Gbest 对比，若当前适应度值优，则更换当前适应度值为全局最优位置.

(4)按照公式(7)和(8)对粒子的速度和位置进行动态调整

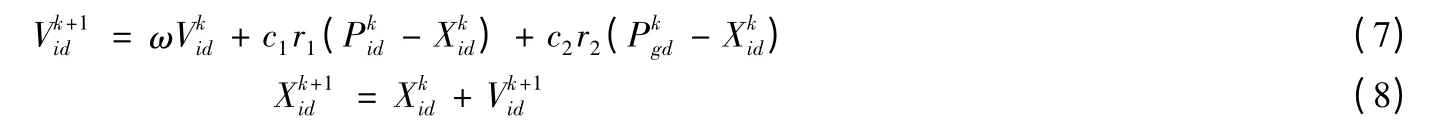
公式中:ω 表示为惯性权重;d=1，2，…，D;i=1，2，…，n;k 为迭代次数;Vid为粒子的速度;c1，c2为加速因子;r1，r2是介于0 到1 之间的随机数.

(5)判断是否达到最优，若满足，输出最优参数值;若不满足，依照步骤(2)－(4)继续迭代.

3 实例分析

以国家统计局和铁路部门提供的的1985－2002年铁路客运量作为原始数据集［7］.首先，对原始数据进行归一化处理，然后将归一化后的数据分成训练集、测试集和检验集.根据训练集数据，建立PSO－SVM 时间序列预测模型，并根据PSO 算法确定SVM 模型参数;最后，将预测值与实际数据对比，验证模型的预测性能.

原始数据集及其归一化结果见表1所列.利用表1 中1985 ～1999年的铁路客运量数据产生训练样本，相邻5年的数据经过归一化处理作为训练样本的输入，第6年经过归一化处理的数据作为训练样本的输出.以1990－1999年的样本为训练样本数据，2000－2002 作为测试样本，具体数据见表2.为了验证模型的有效性，同时选取了传统的SVM 模型进行预测，分别建立粒子群支持向量机预测模型以及传统SVM 预测模型.粒子群算法相关参数设置如下:种群数为20，迭代数为200，加速因子c1，c2初始值分别为1.5、1.7.

表1 原始数据及其归一化表

表2 PSO－SVM 和传统SVM 预测误差比较

表2 为种模型的误差对比结果，从表2 可知，基于PSO－SVM的预测精度优于传统的SVM 模型，这很大程度上取决于PSO 算法对支持向量机参数进行了寻优处理，提高了预测精度

4 结 论

本文提出了基于粒子群算法优化支持向量机的铁路客运量预测方法.通过粒子群算法进行了支持向量机的参数优化，克服了人工选择参数的不确定性，得到了预测性能更好的SVM 预测模型.用铁路客运量数据作为应用算例，同时构建了传统的SVM预测模型，并形成了对比.实验结果表明PSO－SVM的预测效果更好，为铁路客运量预测提供了一种新途径.

图1 PSO－SVM、BP、SVM 拟合值及预测曲线

［1］刘芹.基于最小二乘支持向量机的城市客运量预测模型［J］.混交通与计算机，2007，25(5):50－53.

［2］陈荔，马荣国.基于支持向量机的都市圈客运量预测模型［J］.交通运输工程学报，2010，10(6):75－80.

［3］文培娜，张志勇，罗琳.基于BP 神经网络的北京物流需求预测分析［J］.物流技术，2009(6):91－93.

［4］Vapnik W N.统计学习理论的本质［M］.张学工，译.北京:清华大学出版社，

［5］Venkoba R B，Gopalakrishna S J.Hard grove grind ability index prediction using support vector regression［J］，International Journal of Mineral Processings，2009，91(12):55－59.

［6］Liu Sheng，Li Yanyan，Anovel predictive control and its application on water level system ship Hoiler［C］.International Conference on Innovative Computing，Information and Control，2006:8.

［7］中国国家统计局.中国统计年鉴［M］.北京:中国统计出版社，1985－2003.