单亲遗传算法在电力计量器具配送问题中的研究
尹 飞,李新家,祝永晋
(江苏方天电力技术有限公司,江苏 南京 211102)
物流配送车辆调度问题作为一个完全多项式非确定性(NP)难题,随着客户数量和车辆数量的增加,可选的车辆路径方案数量将以指数速度急剧增长,穷举法在生产环境中已经不可能再使用。因此,用启发式算法求解该问题成为研究的一个重要方向。求解物流配送车辆调度问题的方法很多,常用的有旅行商法、动态规划法、节约法、扫描法、分区配送算法、方案评价法等。遗传算法的出现为求解物流配送车辆调度问题提供了新的工具,传统遗传算法能够方便地求得问题的近似最优解,但对复杂问题搜索效率低,易陷入“早熟收敛”的困境[1,2]。单亲遗传算法是对传统遗传算法的一种改进,不使用传统遗传算法中常用的交叉算子,对某个个体的遗传操作只在该条染色体上进行,即只通过单个个体繁殖后代[3]。由于单亲遗传算法不使用交叉算子,即使群体中的个体完全相同,也不影响遗传迭代的进行,从而摆脱了对群体多样性的要求,能克服“早熟收敛”问题。通过选择、染色体重组等遗传操作,使群体一代一代地进化到搜索空间中越来越好的区域,从而获得较优解。文中采用单亲遗传算法来对配送路径进行近似最优解的计算。
1 计量中心电力器具配送问题的数学模型
通用物流配送车辆调度问题可以描述为:从某物流中心用多台配送车辆向多个客户送货,每个客户的位置和货物需求量一定,每台配送车辆的载重量一定,其一次配送的最大行驶距离一定,要求合理安排车辆配送路线,使目标函数得到优化,并满足以下条件:(1)每条配送路径上各客户的需求量之和不超过配送车辆的载重量;(2)每条配送路径的长度不超过配送车辆一次配送的最大行驶距离;(3)每个客户的需求必须满足,且只能由1台配送车辆送货。
在计量中心的环境,设计量中心有K台配送车辆,每台车辆的载重量为 Qk(k=1,2,…,K),其一次配送的最大行驶距离为Dk,需要向L个二级库送货,每个二级库的货物需求量为 qi(i=1,2,…,L),二级库 i到 j的运距为dij,物流中心到各二级库的距离为d0j(i,j=1,2,…,L),再设nk为第k台车辆配送的二级库数量(nk=0表示未使用第k台车辆),用集合Rk表示第k条路径,其中的元素rki表示二级库rki在路径k中的顺序为i(不包括计量中心),令rk0=0表示计量中心,若以配送总里程最短为目标函数,则可建立如下配送车辆调度问题的数学模型:
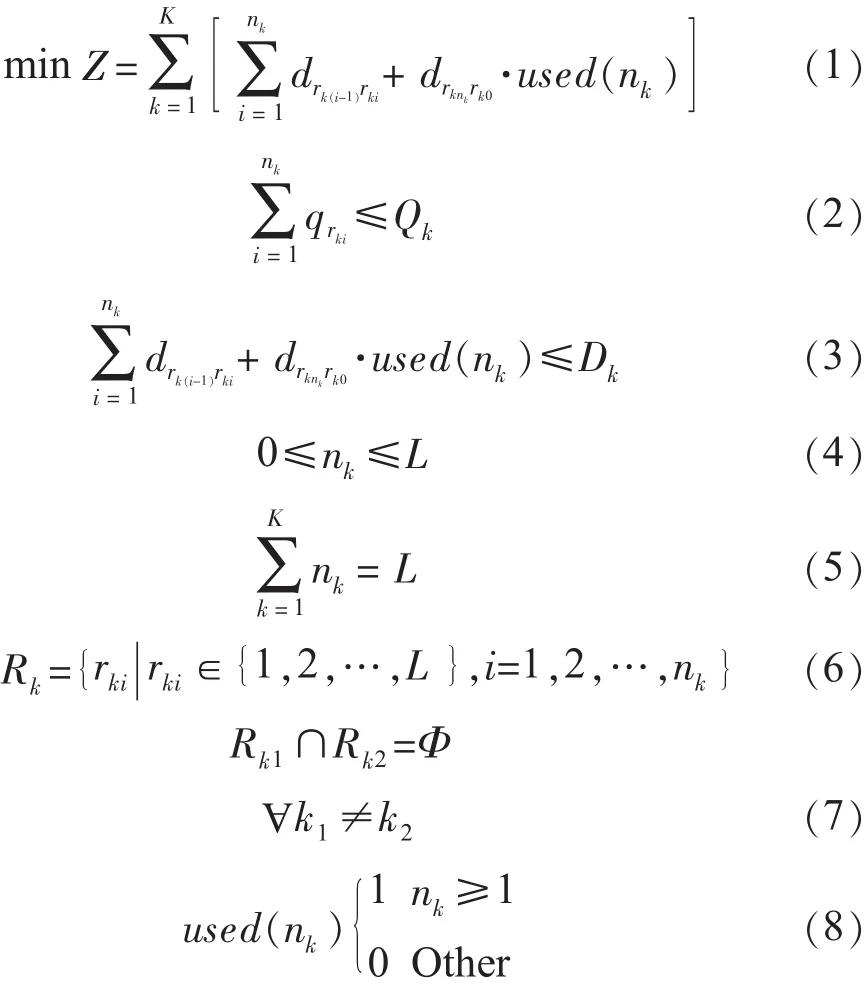
式(1)为目标函数,在文中目标函数为配送里程最短,实际使用可以根据情况变更为油耗最低或速度最快,多个因素综合考虑也是可行的;式(2)保证每条路径上各二级库房的货物需求量之和不超过配送车辆的载重量;式(3)保证每条配送路径的总里程长度不超过配送车辆一次允许的最大行驶距离,行驶距离既可以作为目标函数的约束条件,也可以作为目标函数的运算项。实际使用中这一约束条件也可以变更为每辆车单次行驶时间,或移除此约束;式(4)表明每条路径上的二级库房数不超过总二级库房数;式(5)表明每个二级库房都得到配送服务,实际使用中可以将本次不进行配送的库房移出计算表格,这样不必修改此约束条件;式(6)表示构造各条路径的二级库房的组成;式(7)限制每个二级库房仅能由1台配送车辆送货,如果二级库房需求量较大,需要多辆车进行配送,此条件也可以放宽。但是从省中心的物流管理的目标来看,小批量多批次的配送方式将可能成为主流,故此约束具有现实意义;式(8)表示当第k辆车服务的二级库房数不小于1时,说明该台车参加了配送,则used(nk)取1,当第k辆车服务的客户数小于1时,表示未使用该台车辆,used(nk)取 0。
2 算法的构造
2.1 编码方法的确定
根据计量中心配送车辆调度问题的特点,文中采用简单直观的自然数编码方法[3],用0表示配送中心,用1,2,…,L表示各提出需求的二级库房。由于在计量中心有K台车辆,则最多存在K条配送路径,为了在编码中反映车辆配送的路径,通过增加K-1个虚拟计量中心的方法,分别用 L+1,L+2,…,L+K-1表示,将这些虚拟计量中心的整数加入原配送点集合,L+K-1个互不重复的自然数的随机排列就构成一个个体,并对应一种配送路径方案。例如,在一次配送中需要用3台车辆对9个二级库房进行配送,则可用1,2,…,11(1-9表示各二级库房,10,11表示计量中心,在实际计算中与0等同)这11个自然数的随机排列,表示物流配 送 路 径 方 案 , 如 个 体 “1,8,6,11,3,2,4,5,10,7,9”表示的配送方案为:路径 1,0-1-8-6-11(0);路径2,11(0)-3-2-4-5-10(0);路径 3,10(0)-7-9-0,需 3台车辆配送。前后分别加入的0表示,车辆最终需要返回计量中心。
2.2 初始群体的确定
随机产生1至L+K-1这L+K-1个互不重复的自然数的排列,即形成一个个体。设群体规模为N,则通过随机产生N个这样的个体,即形成初始群体。规模在很大程度上决定了遗传算法寻找到最优解的可能性,但规模达到一定程度之后,再增加初始群体的规模则对结果影响很小,呈现侧抛物线的形状。选择范围一般会随配送路径点的总数量变化而进行调整,总的来说不会小于500。
2.3 适应度评估
对于某个个体所对应的配送路径方案,要判定其优劣,一是要看其是否满足配送的约束条件;二是要计算其目标函数值(即各条配送路径的长度之和)。
由于文中根据配送路径选择问题的特点所确定的编码方法(整数序列),隐含能够满足每个二级库房都得到配送服务,且每个库房仅由1台车辆配送的约束条件,但不能保证满足每条路径上各库房的总需求量不超过汽车载重量及每条路径的长度不超过汽车单次配送的最大行驶距离的约束条件。为此,对算法中产生的每个配送方案,要对各条路径逐一进行判断,看其是否满足上述2个约束条件,若不满足,则将该条路径定为不可行路径 (可以惩罚权重的方式来进行设定),最后计算其目标函数值。对于某个个体j,设其对应的配送路径方案的不可行路径数为Mj(Mj=0表示该个体是一个可行解),其目标函数值为Zj,则该个体的适应度Fj,可用下式表示:

式中,Pw为对每条不可行路径的惩罚权重(该权重可根据目标函数的取值范围取一个相对较大的正数)。之所以使用惩罚权重,而不是直接将该不可行路径移除是考虑到在基因突变的过程中,不够优秀甚至不可行的父代也有可能产生优秀的子代。
在省中心的实际使用中,以插件的方式加入更多的约束条件,使适应度评估更具实用性。如某2地之间的高速公路正在做短期维护导致路堵严重,则可以临时添加1个约束条件,不允许走这条路径。
2.4 选择操作
将每代群体中的N个个体按适应度由大到小排列,排在前几位(参数G)的个体性能最优,将它们直接复制进入下一代,并排在前位。下一代群体的其余个体的产生,则需要根据前代群体的N个个体的适应度,采用赌轮选择法产生。具体地说,就是按上代群体中各个个体的排名以轮盘法计算其被选择的概率。这样既可保证最优个体生存至下一代,又能保证适应度较大的个体以较大的机会进入下一代,同时允许部分劣质个体在突变后产生优质个体后进入下一代,避免过早收敛的问题。
2.5 染色体重组
对通过选择操作产生的新群体,除排在前G位的最优个体外,另N-G个个体要运用单亲遗传算子进行染色体重组。文中选用多点基因换位算子实现染色体重组,现举例说明其操作过程:
(1)设定基因换位次数(Nt),本例中设 Nt为 1。
(2)在染色体上随机选取Nt对基因,并交换其位置。本例中设原染色体A为478563921,随机产生的第一对交换基因位为3和7,则基因换位后染色体A'变为438567921。
(3)判断在基因换位后个体的适应值是否增加,若增加,则用新的个体取代原个体,进入下一代,否则原个体直接进入下一代。
(4)本例中设A'的适应值大于A的适应值,则A'进入下一代。
2.6 终止准则
基因进化一般使用的终止准则包括以下几种:(1)进化次数限制;(2)计算耗费的资源限制(例如计算时间、计算占用的内存等);(3)一个个体已经满足最优值的条件,即最优值已经找到;(4)适应度已经达到饱和,继续进化不会产生适应度更好的个体;(5)人为干预;(6)以上2种或更多种的组合。文中使用进化次数限制来进行终止。
3 运行效果和参数设置分析
为了测试算法的效果,构建一个虚拟的环境,共有9个二级库房,分配了3辆车(最大容量均为1)进行配送,分别采用穷举法、节约法以及单亲遗传算法进行最优路径求解。库房间里程以及需求数量如表1所示。

表1 库房间里程及要求
3.1 穷举法
在测试用机(普通双核)上,通过全排列的方式进行穷举,全部路径数量为39916800条,最佳路径长度为1072.6 km,用时为15 s。如果是范围增加到13个二级库房,用时将会增加到466830 s。即使运行在小型机上,计算用时也是无法承受的。
3.2 节约算法
采用节约算法,可以得到如表2所示的配送方案。配送总里程为1295.6 km,配送车辆数为3台。
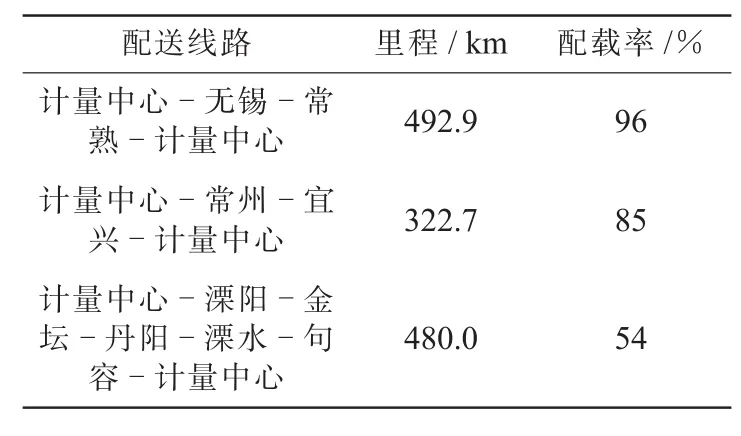
表2 节约算法配送方案
3.3 单亲遗传算法
定制化的单亲遗传算法参数设定:初始群体数量1000,进化次数40,基因换位次数1。运行10次之后,结果如表3所示。
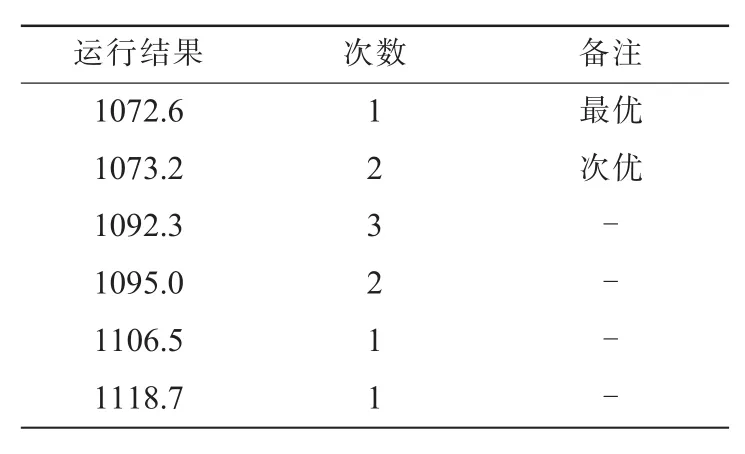
表3 单亲遗传算法结果
平均每次计算用时为0.03 s,其中有1次为最优解,2次为次优解,其他解也比节约法的结果要好。其次优解配送路线如图1所示,配送方案如表4所示。
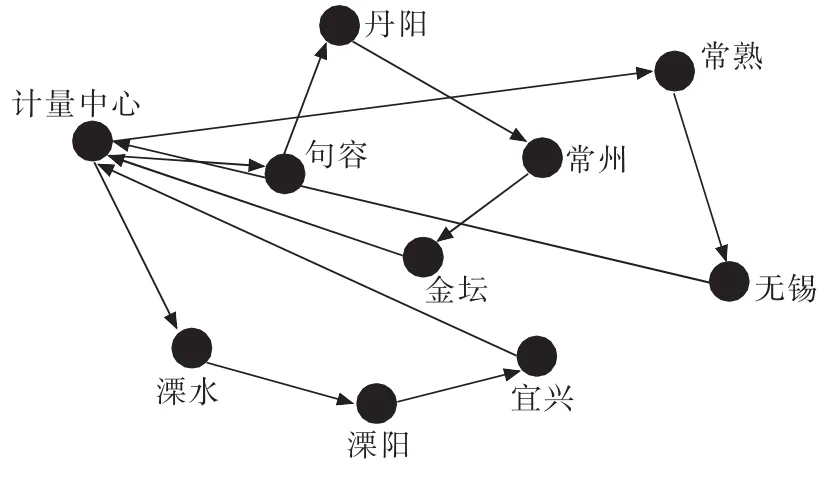
图1 单亲遗传算法次优解配送路线
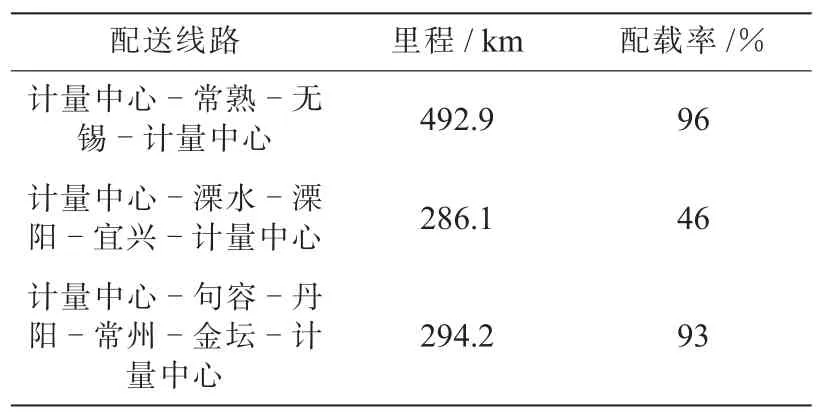
表4 单亲遗传算法次优解配送方案
3.4 结果比较
穷举法虽然必然能得到最优解,但由于效率原因不适用于生产环境。节约算法效率较高,但随着运输节点的增加,其寻优能力下降明显。单亲遗传算法不仅性能好,而且在寻优方面的表现明显超过了节约法。
3.5 参数设置分析
进化次数和初始群体的大小均会对遗传结果产生影响:初始群体数量如果太大,则会大大增加运算时间;如果较小,则需要更多的进化次数来弥补。
需要注意的是,初始群体的合适范围实际上与总的可能路径数量有关。当总路径数量在4000万条时,初始群体数量在1000左右即可满足要求,而总路径数量达到4亿时,初始群体要达到4000左右才能满足要求。应避免因样本太少,相对于全局来说收敛过于快速,从而忽略了最优解。以计量中心全部72个二级库房,使用20辆车来进行配送,预计初始群体需要达到10万,进化次数达到4000,计算结果就可以达到令人满意的效果。
若对最优解有较为强烈的要求,则应该设置一个中等的初始群体大小和进化次,再进行多次运算。
3.6 扩展应用
在实际使用中,可以采用插件的方式对算法进行定制,如将平均等时间加入到适应函数中,也可以动态地加入路况信息以得到更合理的配送路径[4]。同时由于单亲遗传算法的效率非常高,故而可以在情况不明确(如配送车辆的数量,配送频率不确定)的情况下,进行多次计算,从而为不同的配送方案的评估提供参考信息。
4 结束语
在充分分析计量中心配送车辆调度需求的基础上建立了数学模型,不仅解决了传统遗传算法容易“早熟收敛”的问题,而且创新地采用了插件方式,更容易在求解过程中进行动态的约束添加,从而进一步提高算法可用性的寻优能力。算法的计算结果也表明了该算法不仅性能卓越,而且其寻优性能非常突出。文中构造单亲遗传算法的思路是以整数编码方式为基础,添加了虚拟中心仓库来构造完整的路径表达式,该方法不仅可以在路径计算中使用,也可以作为求解其他组合优化问题的参考。
[1]SZCZERBICKAH,BECKERM,SYRJAKOWM.Genetic Algorithms:A Tool for Modelling,Simulation and Optimization of Complex Systems[J].Cybernetics and Systems,1998,29(7):639-659.
[2]SCHMITT LOTHAR M.遗传算法理论,Theoretical Computer Science(259),2001:1-61.
[3]SCHMITT LOTHAR M.遗传算法理论(二),Theoretical Computer Science(310),2004:181-231.
[4]曹一家.并行遗传算法在电力系统经济调度中的应用—迁移策略对算法性能的影响[J].电力系统自动化.2002,26(13):23-27.

