SVC电压稳定控制和抑制低频振荡交互影响研究

王云洁，胡 弢

(1.东南大学电气工程学院，江苏 南京，210096；2.盐城供电公司，江苏 盐城，224005)

随着我国西电东送、南北互联和全国联网的战略实施，为提高输电的能力和提高系统稳定性，我国输电系统引进了静止无功补偿器（SVC），分别装设在广东江门、湖南云田、湖北凤凰山（2套）、河南小刘以及辽宁沙岭的500kV变电站和鞍山红一变中，这些示范工程投运对电网运行产生明显的效果，对系统的稳定运行产生积极作用[1]。传统的电力电子控制装置在电力系统中的控制目标通常只有一个，如潮流控制、电压控制或增强系统稳定性等。而在SVC电压环加入附加信号可以同时提供电压支持和阻尼控制，其特点是电压和阻尼控制的双重功能。近几年来，多柔性交流输电系统（FACTS）间的交互影响问题正在研究中。文献[2]指出了PSS与SVC的交互影响并对其进行了多目标协调设计，但是对于单FACTS器件的不同控制目标间的交互影响很少有深入研究；文献[3]分析了静止同步补偿器多目标协调控制。文中从理论上分析了SVC 2种功能间的交互影响，建立了装有SVC的二区域四机系统的模型，通过仿真验证了以上分析研究的有效性。

1 SVC控制作用

1.1 SVC的电压控制作用

SVC的电压控制可用1个简化的SVC和电力系统的框图来表示（见图1）。其中系统等效阻抗对应于SVC母线端的短路容量，关系式为：

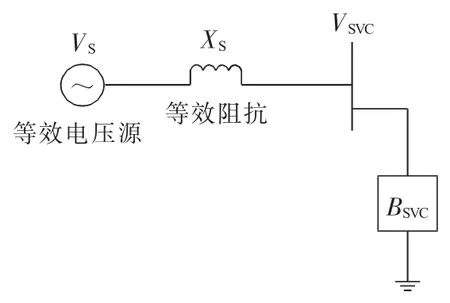
图1 简化电力系统框图

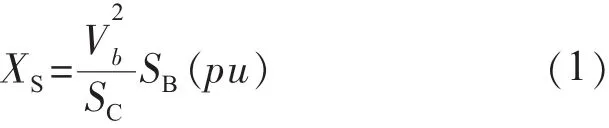
式中：XS为系统等效阻抗；SC为SVC母线三相短路容量；Vb为线电压基准值；SB为系统基准容量。如果SVC吸入无功电流ISVC，无SVC电压调节时，SVC母线的电压为：

可见SVC电流导致了与系统电压同相位的电压降。SVC母线电压随着SVC感性电流的增加而减小，随着容性电流的增加而增加。式（2）反映了系统特性和系统负荷线的关系，意味着在一个弱的交流系统中（高值）SVC电压控制作用比在一个强的交流系统中 （低值）更为有效[3]。

1.2 SVC附加阻尼控制抑制低频振荡作用

SVC具有电压控制功能，在纯粹进行电压控制时基本没有提高系统阻尼的作用，应增加附加控制器来实现阻尼控制[4]。附加阻尼控制器可用相角补偿原理，降低区域间振荡能量从而实现阻尼控制，设计的具体步骤为：（1）对系统进行小干扰分析，分析系统低频振荡特征根，进而分析系统的振荡模式；（2）在相应的振荡频率下，计算滞后角α；（3）计算附加控制器的超前滞后角φ，确定超前滞后控制参数。

SVC及其附加阻尼控制作用原理[5]。单机无穷大系统如图2所示，SVC将中点电压调节到Vm。假设送端的电压保持恒定，即ΔV1=0，则发电机的经典二阶模型为：

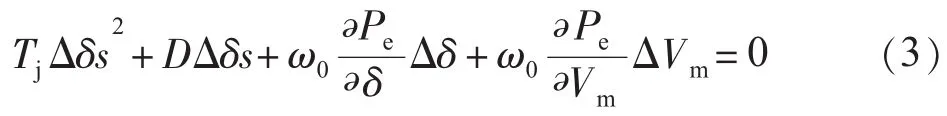
图2 装有SVC的单机无穷大系统

式中：Tj为发电机惯性时间常数；D为系统的自然阻尼功率系数；δ为发电机功角；ω0为发电机同步速；Pe为发电机电磁功率。式（3）描述了系统的小信号动态行为。如果SVC严格按照保持中点电压Vm恒定的控制方式运行，则ΔVm=0，发电机的经典二阶模型为：

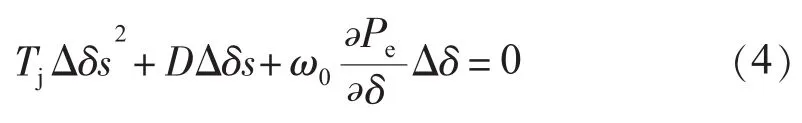
D一般情况下可以忽略，故式（4）对应特征根方程式的根实部为0，导致转子角作不衰减振荡。由式（4）可以看出，按恒定电压控制方式运行时不能提供任何系统阻尼[6]。然而，如果允许对中点电压进行调制，即可以对系统阻尼做出贡献。若中点电压，K为常数，则：

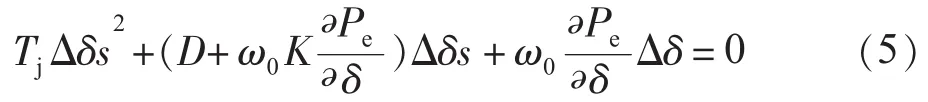
引入附加控制器对电压进行适当调制后，SVC将系统转化为一个具有正阻尼的系统。从式（5）可以看到，新特征根实部为负，转子角的任何振荡都会随时间而衰减。这种控制特性被称为附加阻尼控制。

2 SVC电压控制与阻尼作用间的交互影响分析

SVC附加阻尼控制后能有效抑制低频振荡[7，8]。图2所示的单机无穷大系统中，SVC的作用相当于在中间母线处并联了一个可变电纳，改变了整条线路的等效阻抗。

未安装SVC时，发电机输出的有功功率为：

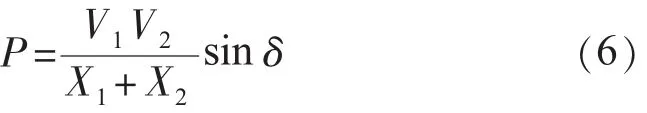
装设SVC后，发电机输出有功功率为（利用Y-Δ变换）：

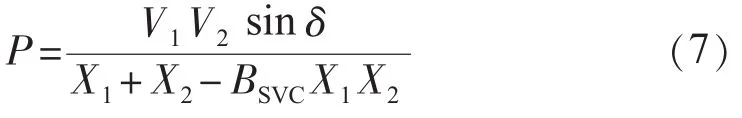
调节SVC的输出，使SVC的并联电纳变化ΔBSVC，则有功功率的增量ΔP为：

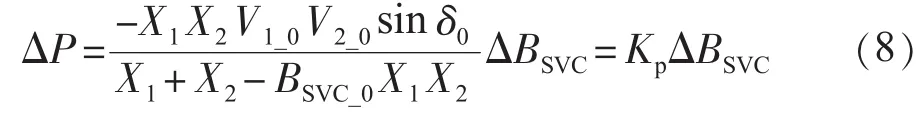
式中：V1_0，V2_0，BSVC_0分别为 V1，V2，BSVC的初始值。SVC安装处的母线电压为：

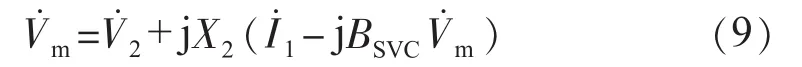
解得：

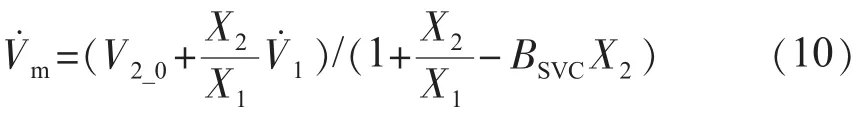
调节SVC的输出，使之变化ΔBSVC，则SVC母线电压的增量ΔVm为：

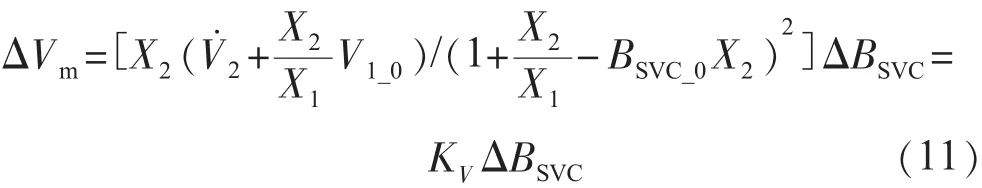
由式（8）可得，SVC附加控制产生的发电机电磁转矩为：

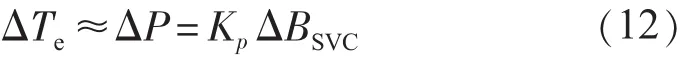
由文献[9]可知，ΔTe由2个分量组成：

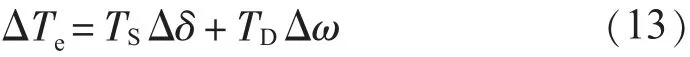
式中：TS为系统的同步转矩系数；TD为阻尼转矩系数。将其代入式（5）并简要写出其特征根方程：

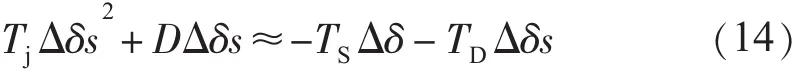
所以TS主要影响振荡频率，而TD主要影响系统机电振荡的稳定性。为保证阻尼控制的效果，要产生大的阻尼转矩，ΔBSVC需增加较大。而ΔBSVC的增加会使ΔVm变大，从而母线电压发生较大的振荡，影响电压控制效果。因此，SVC的阻尼控制与电压控制存在矛盾，增强系统阻尼振荡的能力会降低电压的控制水平。

3 仿真分析

3.1 仿真模型

文中采用2区域4机系统进行仿真，（如图3所示），SVC装置安装于节点8。

图3 2区域4机系统接线

3.2 SVC电压控制仿真

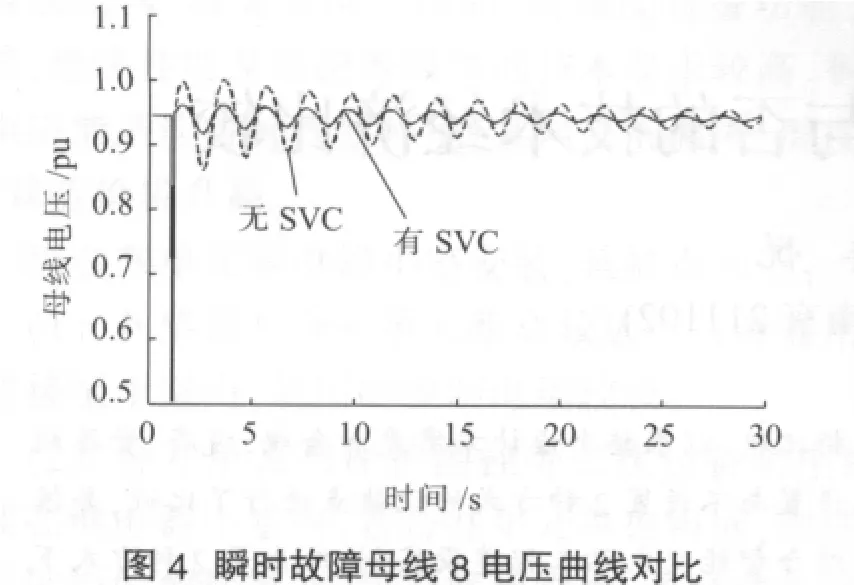
在仿真系统中加入SVC，验证其对电压稳定控制的作用。仿真方案：节点8处1.0 s发生瞬时三相短路故障，1.1 s故障解除。仿真时间为30 s，安装SVC前后节点8电压幅值曲线如图4所示。

从图4的电压曲线可以看出，未安装SVC的情况下，故障消失后系统电压的波动比较大；而加装SVC后，系统电压波动有所减弱，并能较快达到稳定。

3.3 SVC附加阻尼控制抑制低频振荡仿真

对系统进行小干扰稳定分析，发电机1、2和3、4区域间低频振荡模式特征根为-0.053194+j3.401198，其阻尼比小于2%，需要利用SVC的附加阻尼控制器进行抑制该低频振荡模式。在附加控制信号输入处输入一个区域振荡频率的正弦量，其频率与低频振荡模式相同，ω为3.4016。分析由此信号引起的联络线上功率的振荡，通过对比得到滞后角α约为88°。由于两级滞后，附加控制器的超前滞后角φ=（180-α）/2=46°。 由此可得：t1为 0.12 s，t2为 0.73 s。

在系统中仿真验证SVC及其附加控制的阻尼效果。仿真方案：利用电力系统分析综合程序（PSASP）的小扰动分析功能，对不同控制情况下的系统进行小扰动稳定分析，得到低频振荡特征根的变化如表1所示。

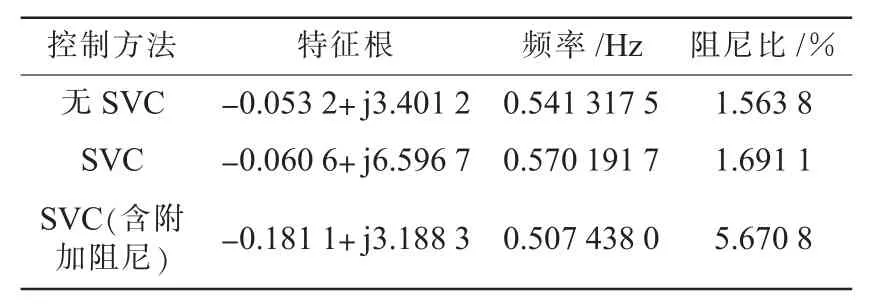
表1 不同控制情况下的振荡阻尼比

由表1可知，无附加阻尼控制的SVC对系统低频振荡的阻尼比基本没有影响；加装附加阻尼控制之后，阻尼比有明显提高，从1.56%左右提高到了5.67%。可见SVC加装附加阻尼控制器能更好地增加系统阻尼比，抑制低频振荡。

3.4 SVC附加阻尼控制对电压稳定的影响仿真

仿真方案：节点8在1.0 s至1.1 s间发生瞬时三相短路故障，仿真时间为30 s，安装SVC前后节点8电压幅值曲线如图5所示。

对比可知，无SVC的情况下系统电压的波动比较大；在加装无附加控制的SVC后，系统电压波动有所减弱，特别在故障瞬间，电压有一个比较明显的上升过程；加装带有附加阻尼控制的SVC后，在故障消失开始一段时间，电压的波动比较大，甚至比未装SVC情况下的电压波动更大，这从前面的理论分析中也可看到，未装SVC时，三相短路发生后，电压瞬间降低到接近0，当故障切除后，电压振荡回复到稳态。而加了附加阻尼控制后，其作用使电压波动变得更大。

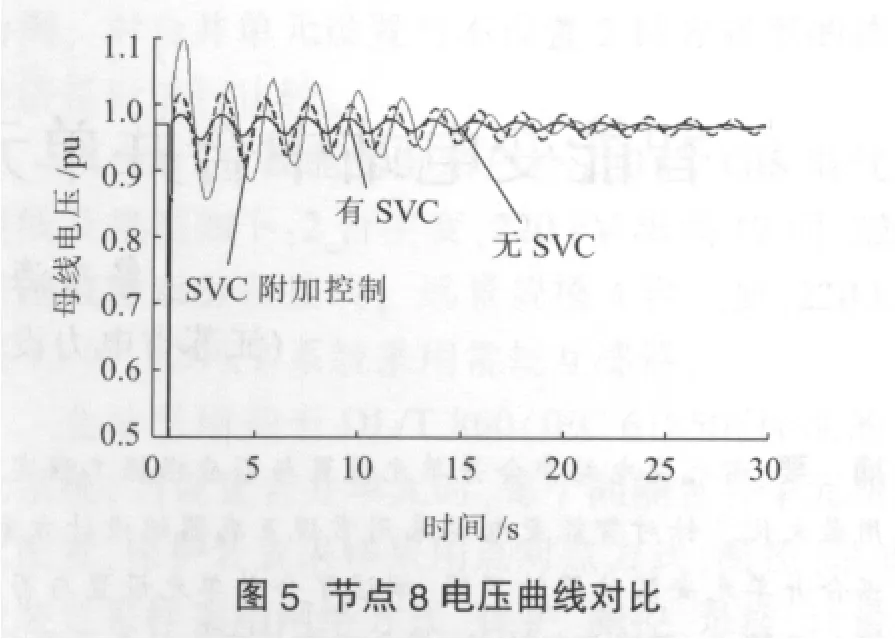
从以上的现象看，SVC的电压控制与阻尼控制之间存在负的相互作用。

4 结束语

研究了SVC电压控制与抑制低频振荡功能之间可能存在的交互影响问题。在研究SVC的电压控制功能及SVC附加阻尼控制对电力系统低频振荡的抑制的基础上，明确了SVC按恒定电压控制方式运行时不能提供系统阻尼，只有附加阻尼控制才能向系统提供正阻尼。而附加阻尼控制提高系统阻尼的同时，理论上对电压控制的稳定性又有不利影响，从而得出SVC的两种控制功能间存在负的交互作用的结论。并在PSASP中进行了时域仿真，证明了SVC电压控制与阻尼控制间存在负的交互影响。

[1]邹振宇，江全元，张鹏翔，等.PSS与SVC多目标协调设计[J].电力系统及其自动化学报，2005，17（4）：66-70.

[2]刘宪林，王 鑫.单机-SVC-无穷大系统机电模式阻尼特性分析[J].郑州大学学报(工学版)，2007，8（3）：89-90.

[3]栗 春，姜齐荣，王仲鸿，等.静止同步补偿器多目标协调控制器的设计[J].电工技术学报，1999，14（2）：21-59.

[4]严伟佳，蒋 平.抑制区域间低频振荡的FACTS阻尼控制[J].高电压技术，2007，33(1)：189-192.

[5]张彦魁，张 焰.静止无功补偿器建模及其在电压稳定研究中的应用[J].上海交通大学学报，2007，41（3）：488-496.

[6]李 林，康积涛，刘永江，等.电力系统小扰动电压稳定性的研究现状及展望[J].电气技术，2010（6）：6-8.

[7]ABIDO M A,ABDEL-MAGID Y L.Analysis of Power System Stability Enhancement via Excitation and Facts-Based Stabilizers[J].Electric Power Components and Systems,2004，32（1）：75-91.

[8]LERCH E,POVH D,XU L.Advanced SVC Control for Damping Power System Oscillations[J].IEEE Transactions on Power Systems，1991，6（2）：524-535.

[9]倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析[M].北京：清华大学出版社，2008.