连通管动态液压力学分析
刘夏平, 孙 卓, 杨 红, 程景扬, 刘爱荣
(广州大学1.土木工程学院;2.物理与电子工程学院,广东 广州 510006)
桥梁挠度变形是评价桥梁使用功能和安全性的重要指标.应用于桥梁挠度测量的连通管位移监测系统由管道、液体以及传感器等组成,主要分为以液位和液压为测量对象的两种方法,通过在结构中安装充满液体的管道,测量液体的液位或液压改变量而获取结构位移.由于其具有精度高、不受多方位变形及现场恶劣环境影响等特点,且在经济性、耐久性等方面有明显的优势,近年来在地面沉降、大坝变形和桥梁结构静态监测中得到了广泛应用[1-3].
目前,连通管的应用与研究多以静态测量为前提,针对结构动态位移测量的研究相对较少,仅有部分学者对连通管液位振荡特性,以及管道压强与结构挠度相关性进行了初步探讨[4-6].应用于桥梁结构的压力场连通管位移监测系统,是通过测量连通管压强而获取桥梁挠度,由于动态挠度测量时,连通管压强变化量不仅与管道位移量有关,且与管道运动方式及其方向密切相关,因此,开展连通管液体动态压强的研究,对于拓展连通管系统应用范围、提高动态挠度测量精度,准确评估桥梁工作性能,具有重要的意义.
本研究根据连通管的基本原理,基于结构动力学理论,建立了连通管内液体动态压强理论计算公式,揭示了连通管动态液压与结构振动加速度及管道倾角之间的关系,并通过模型试验验证了理论公式的正确性.
1 压力场连通管位移监测系统原理
压力场连通管位移监测系统是根据连通管的基本原理,利用水箱、水管以及城市供水在桥梁结构需要监测的位置建立压力场,水箱按照设计高度要求固定在高程不变处,水管沿桥梁梁体纵向铺设并固定在梁体侧壁上,在需要被监测的点布设压力变送器,如图1所示.当桥梁结构在环境或其他荷载作用下产生变形时,固定在其上的管道将随着结构一起变形,而固定位置的水箱内液位高度是不变化的,因此管道压强必然改变[7].

图1 压力场连通管位移监测系统原理图Fig.1 Hydraulic Bridge Displacement Monitoring System
若某测点的管道随桥梁结构产生位移l1,则根据流体静力学原理,该测点管内静态压强改变量(也称为压力差)为:

式中:ρ—管内液体密度;g—重力加速度.
通过压力变送器采集压力差ΔF1,并转化成模拟信号,再经采集系统转化成桥梁位移信号的变化.
2 连通管动态液压分析
2.1 连通管的力学模型简化
连通管一般沿桥梁上部结构布设,且设有多个测点.对于长大跨和高落差桥梁,受结构限制,假定管道与水平线成一倾角φ布置,为简化分析,且不失普遍意义,采用管内液体为水的单一测点连通管液压力学分析模型,如图2所示,并建立如图所示的坐标系,坐标原点设在管道最低点.
2.2 连通管力学分析
当固定在梁体上的连通管作上下竖直振动时,假定振动加速度沿管道轴线分布函数为a(x),为迫使管内水体与管道共同协同运动,管道将对管内的水施加竖向压力p(x),压力的方向与加速度的方向相同(见图3).
根据牛顿第二定律,水体受管道作用力p(x)的大小与其质量m成正比:

上式是矢量表达式,其沿管道轴线上的分量式为:

因管道以加速度a(x)振动而导致测点管内水体沿管道轴线方向的压强改变量为:

式中,x1、x2分别为测点及管道中部至坐标原点的距离,A为管道截面面积.
由于dx长度水体质量dm=Aρdx,故上式可整理为:

上式为桥梁结构振动加速度产生的连通管内压强变化量.因此,由结构振动导致的连通管动态液压应为位移引起的ΔF1和加速度引起的ΔF2两项之和,即:


图2 连通管动态力学模型Fig.2 Dynamic Mechanics Model of Connecting Pipe

图3 液体加速度及受力示意图Fig.3 Liquid Acceleration and Vertical Force
3 模型试验
为验证连通管压强与结构振动加速度关系表达式公式(6)的正确性,本研究进行了连通管液压动态特性模型试验.
3.1 试验模型与方法
试验系统由基准桶、门式钢架、钢管、不锈钢板梁以及连接管组成,如图4所示.不锈钢板梁长2.0 m、宽0.1 m、高1.7 mm,两端悬吊在钢架下,构成简支梁;钢管长0.985 m、内径0.02 m,上端封闭,并悬挂于简支梁跨中,钢管倾角为21.24°,下端铰支承.当简支梁在跨中初始竖向位移激励下产生振动时,带动钢管上端振动.基准桶采用直径为0.35 m,高为0.4 m的硬质塑料桶,中部设有2个连接孔,通过连接管分别与钢管上端和压力变送器的低压端相连,下端设有1个连接孔,通过连接管与钢管下端连接;压力变送器的高压端与钢管下端相连.门式钢架与不锈钢板简支梁截面惯性矩之比为25∶1,故可略去钢架的变形影响.基准桶与管道面积之比为306∶1,可以略去钢管振动对基准桶液位的影响[8];为便于在简支梁跨中放置加速度计,测量钢管上端加速度,钢管上端焊接一块钢板.

图4 试验系统实物图Fig.4 Test system photograph
试验前从基准桶开始灌注水,水流经连接管、钢管,以及基准桶中部连接孔流回基准桶,灌注完毕后排出系统内空气.试验开始时,简支梁以跨中初始竖向位移6 cm激励,通过压力变送器测量低压端与高压端的压力差变化,获得钢管下端截面因简支模型梁振动引起的水压改变量,并利用加速度传感器同步测量简支梁跨中竖向加速度.
3.2 试验结果
图5为实测钢管下端压力差及上端加速度时程曲线.从图中可以看出,压力差变化时程曲线与加速度时程曲线具有极高的相似性.实测压力差时程曲线的频率为0.94 Hz,最大幅值为91.9 Pa,加速度频率为0.92 Hz,最大幅值为0.52 m/s2,压力差变化时程曲线频率与振动加速度频率相近,加速度最大时,管道压力差变化也为最大.

图5 实测压力差及加速度时程曲线Fig.5 Actual Acceleration and Pressure Intensity Difference History
4 理论计算值与试验值比较
4.1 理论计算
根据结构动力学,简支梁可简化为有阻尼单自由度体系的动力模型,其运动方程为[9-10]:

式中M、C及K分别为结构的质量、阻尼及刚度;a、v和l分别为结构加速度、速度及位移.由初位移引起的有阻尼自由振动,其初始条件为:

运动方程(7)是一个二阶齐次常系数微分方程,可以用常微分方程的分析方法求解,其满足初始条件的解如下:

式中:l(0)—初始位移;
ωD—阻尼体系的自振频率,
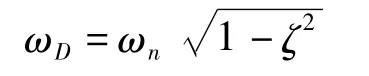
ωn—无阻尼体系的自振频率,
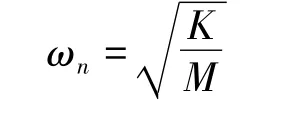
ζ—结构阻尼比.
对上式求二阶导数,则可得到管道上端的振动加速度为:t=0时,管道上端加速度值最大,其值为



钢管下端加速度恒为0,加速度沿钢管长度方向线性分布,与下端截面相距x长度的管道截面最大加速度为:
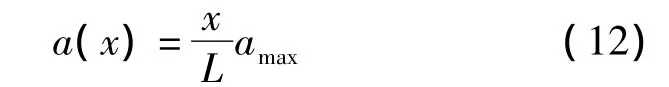
式中:L—钢管长度.
将式(12)代入式(5),则可求出因振动加速度a引起的钢管下端压强变化量:
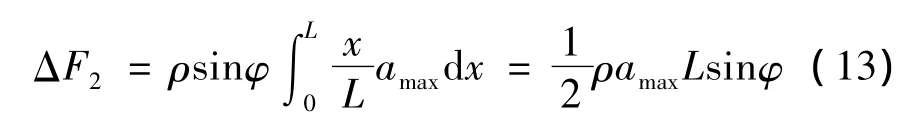
由于钢管下端位移l=0,根据式(13)和(6),钢管下端动态液压为:

将式(11)代入式(14),并考虑压力差以增大为正,则上式又可表示为:

4.2 计算值与试验值比较
采用水密度ρ=1 g/cm3,根据式(15)即可计算钢管下端动态压力差.图6为钢管下端压力差的理论计算值与试验值比较图.从图6可看出,理论计算压力差时程曲线与试验压力差时程曲线吻合较好,压力差最大幅值的理论计算值为90.9 Pa,与试验值的误差仅为1.1%.

图6 压力差计算值与试验值比较Fig.6 Comparison Between Calculated and Actual Pressure Intensity Difference
5 参数讨论
根据压力差计算公式(6),由结构振动导致的连通管动态液压与结构位移量和振动加速度,以及管道布置倾角有关.
结构位移量与管道压强成线性正相关关系,桥梁结构在荷载及各环境因素作用下产生的位移越大,则管道的压力差越大;结构上拱时管道的压力差为负,反之,结构下挠时管道压力差为正.
管道压强不仅与结构振动加速度值有关,还与加速度分布规律有关,结构振动加速度沿测点到主跨跨中分布的总量越大,则管道压力差越大;管道压力差还与结构振动加速度方向有关,结构振动加速度方向向下,则管道压力差为正,反之为负.
管道压力差与管道倾角φ之间成正弦三角关系,φ值越大,则压力差越大.
6 结论
(1)基于结构动力学理论,建立了连通管动态压强理论计算公式,揭示了连通管动态液压不仅与结构位移量有关,还与结构振动加速度,以及管道倾角等参数之间的关系;因此,结构位移量不能简单地由连通管动态液压直接转换,应考虑结构振动加速度和管道倾角等参数的影响.
(2)模型试验结果表明,由结构振动加速度产生的连通管压强最大幅值的理论计算值与试验值的误差在2%以下,验证了连通管动态压强理论计算公式的正确性.
(3)影响连通管压强的主要参数研究结果表明,连通管压强与管道位移量呈线性正相关关系,与管道倾角成正弦三角关系,随测点至主跨跨中截面加速度分布的总量增大而线性增大.
[1] 杨建春,陈伟民.连通管式光电液位传感器在桥梁挠度监测中的应用[J].传感器与微系统,2006,8(28):79-81.
[2] 曾 威,于德介,胡柏学,等.基于连通管原理的桥梁挠度自动监测系统[J].湖南大学学报:自然科学版,2007,7(8):44-47.
[3] 杨建春,陈伟民.桥梁结构挠度自动监测技术的现状与发展[J].传感器与微系统,2006,9(1):1-3.
[4] 刘国平,雷小华,陈伟民,等.连通管位移测量系统U型管模型的动态特性研究[J].传感器与微系统,2007,11(11):41-44.
[5] 张 亮,陈伟民,章 鹏,等.连通管位移测量系统的液位振荡特性[J].振动、测试与诊断,2010,5(16):552-556.
[6] 陈德伟,班新林,李欣然,等.压力场桥梁挠度监测新方法的流体动力学分析[J].水动力学研究与进展,2008,4(5):385-392.
[7] 陈德伟,李欣然,杨文军.桥梁结构安全监测中的挠度测试新方法[C]∥第十六届全国桥梁学术会议论文集(下册).中国长沙:第十六届全国桥梁学术会议,2004.
[8] 李成跃.大跨度拱桥位移监测技术研究[D].重庆:重庆交通大学硕士毕业论文.2008.
[9] 刘晶波.结构动力学[M].北京:机械工程出版社,2005.
[10] 周艳清,陈志刚.汽车荷载作用下铰接板梁桥的空间动力响应分析[J].暨南大学学报:自然科学版,2012,33(3):323-328.

