多拓扑结构五轴机床综合误差建模软件开发

孙名佳

(沈阳机床(集团)有限责任公司 高档数控机床国家重点实验室，沈阳 110142)

0 引言

多轴联动数控机床中，刀具与工件的相对位置决定了机床的加工误差，因此想要对加工误差进行补偿，建立机床空间综合误差模型就显得尤为重要。应用多体系统理论，根据机床结构建立综合误差模型是目前常用且有效的方法。但是该方法计算比较复杂，而且对于不同结构机床需要建立不同的模型。

“多拓扑结构五轴机床综合误差建模软件”集成了目前常见的RRTTT、TTTRR和RTTTR三种拓扑结构的五轴机床综合误差模型，输入机床各项误差元素值后，该软件可以自动计算出刀尖点与工件被加工点的相对位移，即加工误差。

本文介绍了多拓扑结构五轴机床综合误差建模软件开发所依据的基础理论，分析了五轴机床的各项误差元素，并给出了综合误差建模过程及软件的使用方法。

1 机床误差建模原理

多体系统是指由多个刚体或柔体通过某种形式联结而成的复杂机械系统。多体系统理论和方法具有通用性和系统性，非常适合于进行空间误差建模，目前已经在机器人、机床、坐标测量机等复杂机械的运动分析与控制中得到成功应用。

本文采用拓扑结构对机械系统进行抽象简化，如图1所示，用低序体阵列对拓扑结构进行描述，并用4×4齐次矩阵表示多体系统中相邻体间的坐标变换。

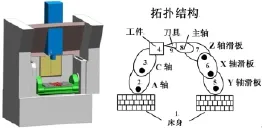
图1 RRTTT型五轴机床简图及拓扑结构图

1.1 低序体阵列理论

设惯性参考系为B0体，选一体为B1体，然后沿远离B1的方向，按自然增长数列，从一个分支到另一个分支，依次为各体编号。用以描述多体系统拓扑结构的低序体阵列通过下列定义的计算公式得到[1]。

任选体Bj为系统中任意典型体，体Bj的n阶低序体的序号定义为：

式中，L为低序体算子，并称体Bj为体Bi的n阶高序体。它满足：

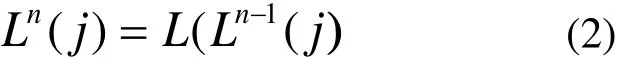
且补充定义：

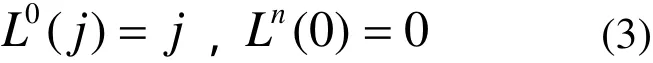
当体Bi为Bj的相邻低序体时，有：

1.2 理想状态的坐标变换矩阵

多轴联动数控机床中，一般包括平移运动和旋转运动，理想状态下，这两种运动的变换矩阵如下：

1）平移运动变换矩阵

任意平移运动可以分解为三个分别沿X、Y、Z轴的基本平移运动。设坐标系Oj-xjyjzj是由Oixiyizi分别沿X、Y和Z轴各平移xij、yij和zij得到，则Oi-xiyizi至Oj-xjyjzj的变换矩阵为：

其中 Tij( M )表示平移运动的坐标变换矩阵。

2）旋转运动变换矩阵

基本的旋转运动包括分别绕坐标轴X、Y、Z的A、B、C 轴转动。其他任何复杂的旋转运动都可以分解成以上三种运动。

以坐标系Oj-xjyjzj是由Oi-xiyizi按C轴正向旋转γij得到为例，Oi-xiyizi至Oj-xjyjzj的变换矩阵为：

其中 Tij(R)表示旋转运动的坐标变换矩阵。

理想的运动可能是既有平移又有旋转，则合成的变换矩阵为： Tij=Tij( R) Tij( M )。

1.3 实际状态的坐标变换矩阵

实际多体系统中，相邻体之间的相对位姿可能包含沿X、Y、Z三个方向的平移误差和转动误差，综合误差变换矩阵为 Δ Tij=Δ Tij( R ) Δ Tij( M)，其中ΔTij为综合误差变换矩阵，Δ Tij( R)为旋转误差变换矩阵， Δ Tij( M)为平移误差变换矩阵。

通常情况下转动误差数值较小，为了方便计算，可做以下化简：

令 sin(Δ θ) = Δθ, c os(Δ θ)=1，其中 Δθ为转动误差。

2 综合误差建模步骤

下面将以某型RRTTT五轴机床为例，介绍综合误差建模过程，其拓扑结构如图1所示，低序体阵列如表1所示。

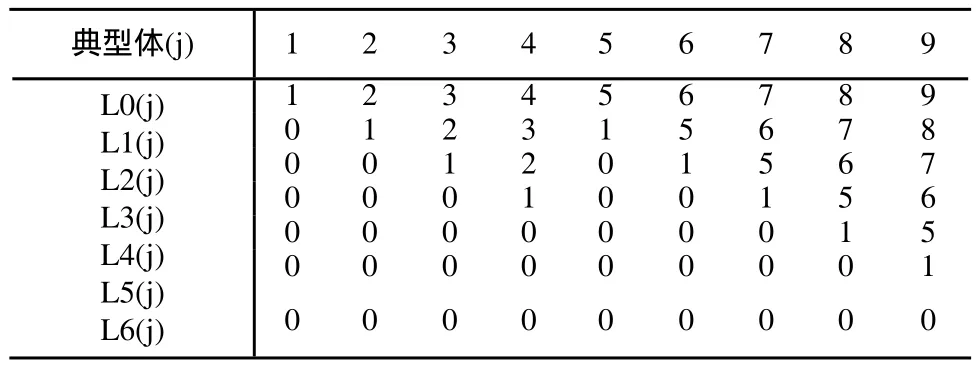
表1 RRTTT五轴机床低序体阵列表

2.1 五轴机床误差元素分析

图1中的五轴机床包含了三个直线轴和两个旋转轴，其中每个轴包含三个方向的平动误差和三个方向的旋转误差，五个轴共包含30项误差，本文还将三个直线轴之间的3项垂直度误差考虑在内，因此本文针对该型五轴机床共考虑33项几何误差。具体如表2所示。

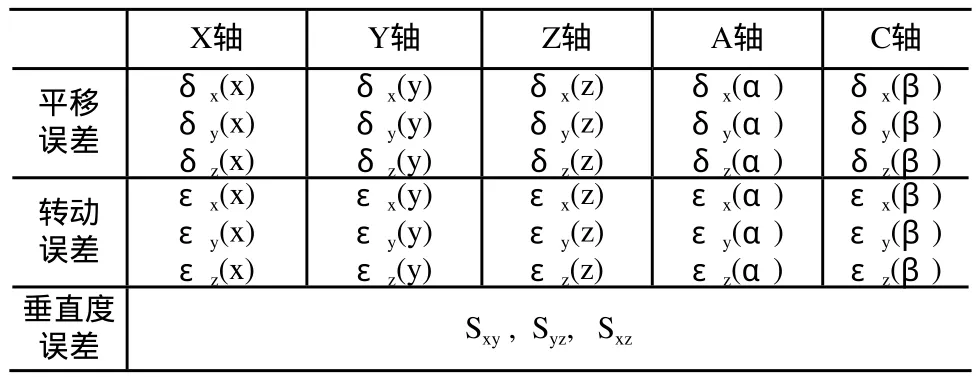
表2 五轴机床误差元素表

其中以X轴为例，δx(x)、δy(x)和δz(x)分别为X轴在当前位置沿X方向、Y方向和Z方向的平移误差；εx(x)、εy(x)和εz(x)分别为X轴在当前位置以X轴、Y轴和Z轴为回转中心的转动误差。其他轴的误差元素定义与之同理。

另外，Sxy, Syz, Sxz分别为X轴与Y轴、Y轴与Z轴、X轴与Z轴间的垂直度误差。

2.2 机床各体间坐标变换矩阵

根据五轴机床各体之间的运动和位置关系，可以得出实际情况下他们之间的坐标变换矩阵，具体如下。其中由于床身相对于大地静止不动，因此床身坐标系与惯性参考坐标系R重合[2]。

1）Y轴滑板坐标系相对于床身坐标系的变换矩阵为：

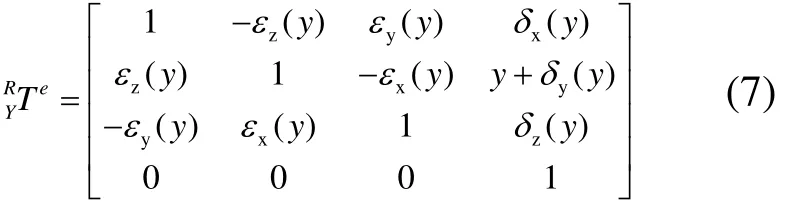
2）X轴滑板坐标系相对于Y轴滑板坐标系的变换矩阵为：

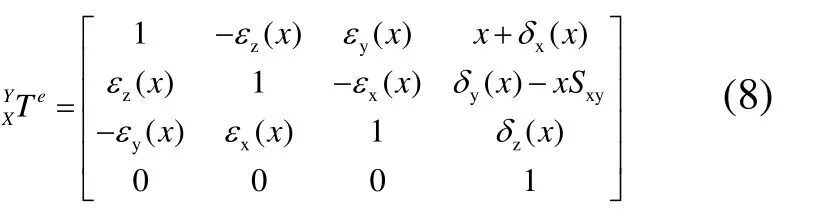
3）Z轴滑板坐标系相对于X轴滑板坐标系的变换矩阵为：

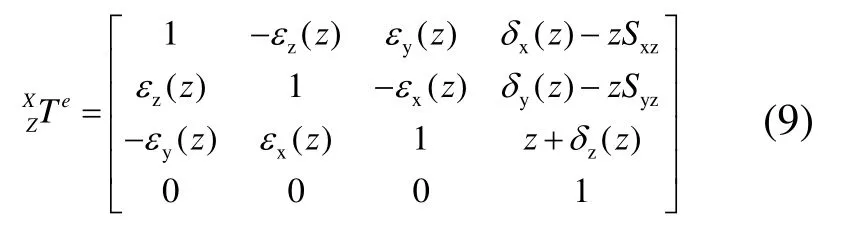
4）主轴相对于Z轴滑板静止不动，因此主轴坐标系S与Z轴滑板坐标系重合，变换矩阵为单位阵I。

5）刀具相对于主轴静止不动，因此刀具坐标系τ与主轴坐标系S重合，变换矩阵为单位阵I。

6) A轴坐标系相对于床身坐标系的变换矩阵为：

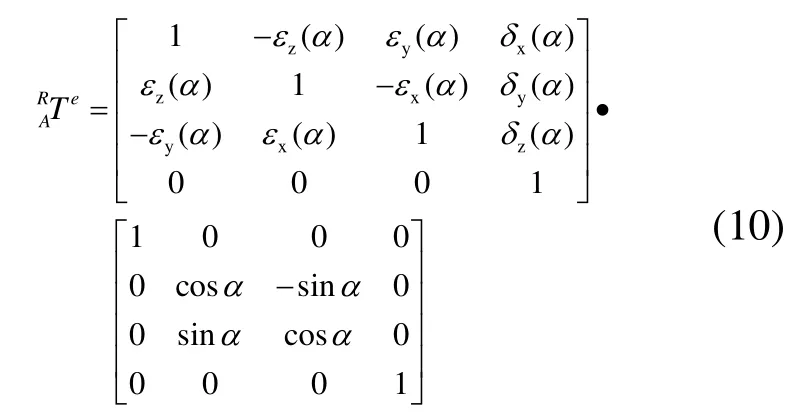
7）C轴坐标系相对于A轴坐标系的变换矩阵为：

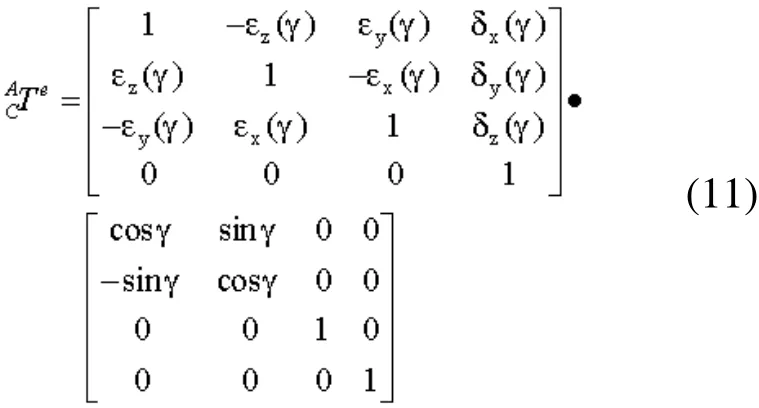
8）工件相对于C轴静止不动，因此工件坐标系w与C轴坐标系重合，变换矩阵为单位阵I。

2.3 综合误差模型的建立

由以上各体间的坐标变换矩阵就可以得出机床综合误差模型。

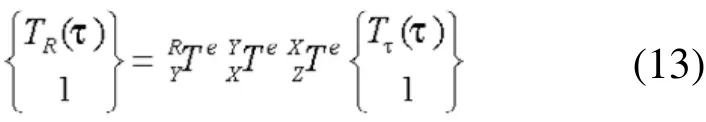
式(14)就是该型五轴机床综合误差模型。

3 综合误差建模软件

根据前面介绍的建模理论和过程，应用Matlab开发了“多拓扑结构五轴机床综合误差建模软件”，如图2所示，该软件集成了RRTTT、TTTRR、RTTTR三种常见五轴机床的综合误差模型，其中TTTRR和RTTTR型五轴机床的建模方法与前面介绍的RRTTT型五轴机床建模方法类似。用户只需要填写机床误差元素值、机床加工坐标等信息，软件就可以自动计算出当前加工误差。

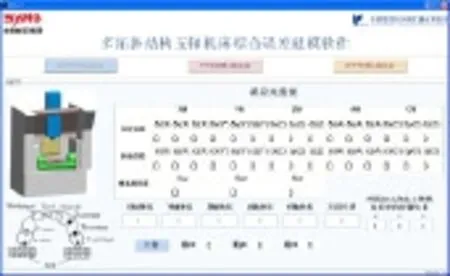
图2 多拓扑结构五轴机床综合误差建模软件

3.1 软件界面介绍

“多拓扑结构五轴机床综合误差建模软件”界面分为四个区域，如图3所示。

图3 综合误差建模软件界面布局

1）区域1-机床类型选择区：用户可以在该区域选择所需机床类型，例如选择TTTRR五轴机床，则点击“TTTRR型五轴机床”按钮即可，选中之后该按钮显示为灰色。

2）区域2-机床类型显示区：显示当前类型机床的简图及拓扑结构图。

3）区域3-参数设置区：用户可以在该区域设置机床误差、加工点坐标、刀具长度和代加工点的位置矢量等参数。

4）区域4-结果显示区：参数设置完成后，用户可以点击该区域的“计算”按钮，加工误差就会显示在Ex、Ey和Ez处。

3.2 软件使用方法

1）首先在软件界面区域1中选择机床类型，例如选择RRTTT型五轴机床。

2）在软件界面区域3中设置误差、机床坐标等参数。其中，误差元素中的平移误差单位是“微米”；转动误差单位是“度”；垂直度误差单位是“度”；各伺服轴坐标值、刀具长度及理论加工点在工件坐标系中的位置矢量单位是“毫米”。

例如设置δx(x)=1.4, δy(y)=2.5, δz(z)=3.3；X、Y、Z、A和C轴坐标分别为100,100,120,0,0；刀具长度为100，理论加工点在工件坐标系中的位置矢量为[100,100,20]。

3）完成以上步骤后，在界面区域4中点击“计算”按钮，软件会自动计算出机床加工误差Ex、Ey和Ez，单位是“微米”，如下图所示。

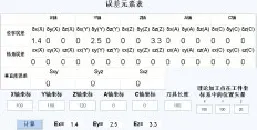
图4 软件计算结果

4 结束语

应用多体系统理论，以拓扑结构描述复杂机械结构，并用齐次矩阵表示各体间坐标变换可以针对多种拓扑结构的五轴机床建立综合误差模型。应用Matlab开发的建模软件，可以方便地计算出五轴机床加工误差，便于机床误差分析和误差补偿等技术研究，因此拥有广阔的应用前景。

[1] 辛立明,徐志刚,赵明扬,朱天旭. 基于改进的多体系统误差建模理论的激光拼焊生产线运动误差模型[J]. 机械工程学报,2010,46(2):61-68.

[2] 李欢玲,缪群华,赵宇,吴洪涛.基于多体系统理论的五轴加工中心几何误差建模[J].中国制造业信息化,2007,36(19): 16-19.