可重构机器人设计理论与研究

陈德林，杨志帮

（开封大学 机械与汽车工程学院，开封 475000）

0 引言

机器人诞生于二十世纪六十年代，其后发展历程长期而漫长，到了八十年代，伴随着以计算机、微电子、互联网为代表的各类技术的迅猛发展，机器人技术也得到了长足的进步[1,2]。由于市场竞争的白热化，行业压力与日俱增，制造系统必须要能适应飞速发展的变化即需要具备柔性制造能力，受限于传统工业机器人的特征性太强，通用性太弱，导致不能实现快速适应各种工况和环境，无法快速响应。与此同时，需求的快速增长，使得在非制造领城，工况越来越复杂，事先很难确定工作环境和工作任务，这就更需要机器人有很强的适应能力，在不同的环境下可以实现可重构，这种可以随时改变构形的机器人被统称为可重构机器人[3～5]。

1 研究背景

可重构机器人的定义为：具备若干个模块，不同的模块之间可以相互连接和分开以实现不同的组合，最终使机器人可以呈现不同的形态和实现不同的功能。可重构机器人的模块的种类虽然不多，一般为1～4类，但是数量却达成百上千甚至上万。每个模块的功能简单，结构单一，但是经过组合之后形成的组合体可以实现之前每个单体无法实现的复杂功能，整体性能有了飞跃性的提升。可重构机器人根据任务的不同来进行形态、姿态和功能重组，比如，在崎岖不平的山路上它化身为多足机器人，在起伏的沙漠里它化身为履带机器人，在城市下水道中，它化身为长条蛇状曲折前进。比起传统的机器人，可重构机器人的优点主要有：高智能化，高适应性，高可靠性，长寿命高稳定性[6]。

2 国内外研究概况

从二十世纪80年代开始，国内外针对可重构机器人开展了大量的研究，目前国内研究领域一般把可重构机器人分为两种：静态机器人和动态机器人，两者的区别主要体现在两个方面：1）前者需要借助外力实现重构，广泛应用于工业领域，又称为工业机器人；2）后者具有很高的人工智能，可以不借助外力实现重构，又称为自重构机器人[7]。

Benhabib开发了一种可重构机器人系统，通过建立模块系统库，实现机器人几何构形的变化和重组，模块系统库主要由三部分组成：connect module，staff system，articulation module。在这个基础上，1979年美国麻省理工学院机器人研究所开发了一种全新的系统RMMS，即可重构机器人系统。作为世界上第一台原理样机，当时被认为是跨时代的一次飞跃，它不仅在机械结构上实现了可重构，同时还在控制器、软件、算法等方面同样实现了可重构。通过进进一步的研究工作，1996年Khosla，Paredis等人进行了系统方面的改进，推出了新型的RMMS，采用了分布控制的方法实现了多样性控制。其中最主要模块为连杆模块以及关节模块，如图1、图2所示。

图1 关节模块图

图2 连杆模块

1989年日本SONY公司研发出了新一代ATRRBUS系统，ATRRBUS系统的主要组成部除了与上述系统类似的连杆模块和关节模块以外，还有全新的控制模块。所有的指令都是通过控制模块实现通讯和传输以实现机器人的每一个动作以及整体控制。

国内对于可重构机器人的探索起步较晚，还处于初级阶段。中科院沈阳自动化所的于苏洋对国内可重构机器人的发展进行了战略前瞻；上海复旦大学的聂爱英依托泛函分析理论，构建了静力学和动力学运动方程，并利用遗传算法进行了模拟推演。天津大学的王琦开发出基于模糊控制的可重构机器人拓扑结构模型。清华大学，北京航空航天大学，北京理工大学，哈尔滨工业大学和中国科技人学也在进行相关内容的研究，成果颇丰。

3 可重构机器人模块化设计

制造技术日新月异，要求制造系统具备柔性化特质，更要求机器人可以适应环境的变化和任务的不同，全世界的研究人员致力于使用各种方法解决此难题，在这中间，模块化设计方法是行之有效的一种，它不仅可以实现快速可重构，而且时间短，成本低，性价比高。

3.1 模块化设计原则

由于机器人的自由度很高，结构复杂，各个自由度支架高度耦合，并非线性变化，因此需要根据功能进行模块的划分，基本原则为：

1）功能独立性：每个模块具备特定的独立功能，实现模块专业化，是可重构设计的基本要求；

2）响应迅速性：可重构机器人的最大特点就是要适应工作任务的不同和工 作环境的改变而变形，这就要求各个模块应该方便拆卸，连接简捷，响应迅速，反应及时；

3）良好驱动性：为了增加传输运动效率，减少能量损失，每个模块都要将惯量减至最小，并且可以自己驱动自己实现本体动作而不依赖于外力，可以有效的降低整体能耗；

4）运动独立性：为了减少耦合性，不同的运动模块之间应该相对独立，降低耦合性对系统的影响；

5）数据自治性：每个模块应该具备独立自治能力，可以实现不同模块之间的实时数据处理和及时上下通讯。

3.2 模块化平台设计

如果要设计可重构机器人的模块化平台，那么我们首先需要知道它构形的变化范围。本文主要研究范围以串联关节结构为主，例如关节型机械臂、仿生腿型机器人。

首先要做的是根据模块划分对机器人的结构进行分析。机器人的基本功能结构图如图3所示。从图中我们可以看到主要的4个功能和对应的4个功能模块。由于实现方式不同，所以可以据此对机器人进行不同的分类，比如以移动机器人为例，如果采用轮式结构实现，则为轮式移动机器人；如果采用关节串联结构实现，则为串联关节型机器人；如果采用仿生腿实现，则为仿生腿移动机器人。以上这些例子是单一功能的实现，真正复杂的机器人应该是两种或者是多种运动功能的叠加，以适应更广泛的应用领域。以下，主要开展关节串联结构移动机器人的研究。

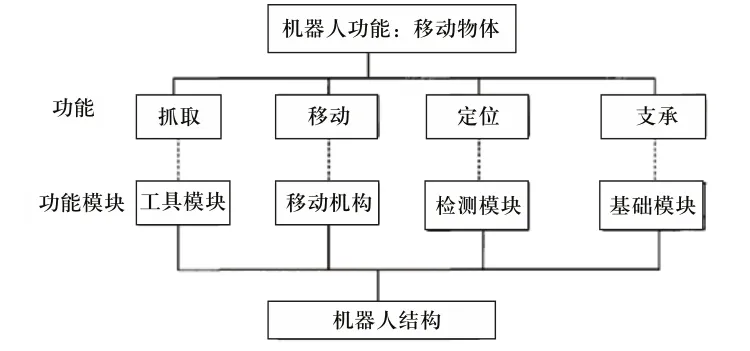
图3 机器人基本功能结构图

要开发出模块化设计平台，就必须采用典型划分方法，利用拓扑结构和自身特征进行分组，首先定义基础模块，在此基础上开发连杆、关节两个并列模块，并衍生出控制类的工具和调节模块。特点需要强调的是调节和连杆两个模块共同组成连接结构，前者用于调节关节轴之间的距离，后者用于调整关节轴之间的角度，两种模块一起作用可以实现关节轴的任意运动。

基础模块是系统的根基，用来定义可重构机器人的整体结构外包络，如图4所示。

图4 基础模块定义整体结构外包络示意图

关节模块是系统的纽带，用来定义任意两关节之间的交叉角度，调整位置和坐标，如图5所示为三种不同类型的关节：垂直转动关节、横向摆动关节和上下移动关节。

图5 三种不同类型的关节模块示意图

连杆模块是系统的桥梁，用来定义两关节之间的最短距离，如图6所示。

图6 连杆模块定义示意图

4 可重构机器人构形设计

4.1 基础构形设计思路

可重构机器人所需要完成的任务可以进行逐级分解，在这里，我们以某个装配任务作为例子进行分析，底层任务是运动路径规划，中间层任务是定位、加紧、加工等工序集合，顶层任务为完成从零件到部组件的装配。所以可重构机器人的基础构形设计思路可概括为：

由问题出发：运动路径规划并发任务拆包分发，借助模块化平台搭建整体可重构模型；

从结果反求：通过模块构建通信控制平台，最终圆满完成给定任务。

4.2 可重构机器人构形设计方法

广义上构形设计问题都可以概括为一类搜索问题，在约束条件和任务目标下，通过搜索目标函数构造最优构形。传统优化方法采用计算代价函数的梯度值，只能得到线性最优解，不满足非线性要求，故本文采用进化算法。进化算法与遗传算法类似，是其的一种演化，它以达尔文的进化论为基础，通过模拟生物自然进化过程来进行求解和自适应，主要通过选择、重组和变异三种手段实现优化问题的求解。

山洪预警指标FFG是指可引发山洪的时段降雨量，在美国通常是指1、3、6小时三个固定的时间段。需要说明的是：FFG是指预报河流断面上游流域上的平均雨量；由于山洪不仅与当前降雨有关，还与小流域下垫面条件、前期洼蓄量、土壤湿度等因素有关，在不同条件下，导致某一山洪沟发生洪水所需的降雨量也不同，因此FFG不是一个固定值，而是一个需要估算的动态变化值。

1）进化算法不需要假设提前解，不需要考虑形式与功能之间的关联，柔性很大，可以完成任意产品的构形设计；

2）进化算法比其他算法能更好的处理离散问题，耦合问题，适用于不同大小的搜索空间，构形设计空间往往是高度耦合的，涵盖离散和连续的变量：

3）进化算法鲁棒性能优越，避免了其他算法往往纠缠于局部最优解的困扰，尽可能的实现全局最优解；

4）进化算法操作简单，运行时间较短，对计算机的硬件需求较低，不需要特别高的配置，具有很好的并行工作能力。

4.3 构形设计实例

在知道了任务要求和得到可重构机器人模块化平台的前提下，即可开展构形设计，前述文中已经讨论过构建模块化平台所需要的四种模块，在后续讨论中，我们只考虑除末端工具模块以外其余的三个：

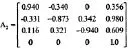
基础模块B的有三个实例：Bml（0.2m），Bm2（0.4m），Bm3（0.8 m），变换矩阵如下，h为高度值：

连杆模块L的一共有10个长度实例，分别为0.05，0.l，0.15，0.2，0.25，0.3，0.35，0.4，0.45，0.5 m。变换矩阵如下，L为高度：

关节模块J有三个实例，变换矩阵如下：

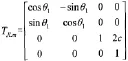
c为关节回转中心到上下两个连接端的长度，2c=0.lm, θ1为回转中心两部分相对转动的角度：

C同上, θ2为横向摆动关节两部分相对转动中心的交叉角度值：

d为上下移动关节模块的移动量，d1为上下移动关节的移动量为初始值时的长度；

输入条件为六自由度串连关节机器人，路径规划为输出端可以快速按预定轨迹移动，位置姿态要求如下所示：

位姿矩阵一：

位姿矩阵二：

位姿矩阵三：

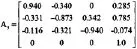
位姿矩阵四：

经过构形设计后，可重构机器人的摹本构形为：

Bm→J→Lm→J→Lm→J→Lm→J→Lm→J→L m→J→Lm→Tool

适应度函数为：

F=exp[-Kl×R+K2×O+K3×V+K4×D+K5×W

+K6R]

进化参数设置为：种群大小为30，最大代数为15，变异概率为0.25，交叉概率为0.7。

运行结果为：Cm02→JSm→Lm09→JRm→Lm 0l→JLm→Lm02→JSm→Lm08→JLm→Lm06→JS m→Tool

5 结论

可重构机器人的构形设计目标在于从在广泛的模块库中寻找和优化出最优的拓扑模型，从本质上来讲是一种以任务为前提的优化求解过程。

本文通过分析可重构机器人构形设计问题的特点，开展了理论研究，并对构形设计问题进行了量化说明，采用遗传算法开展构形设计，有效地实现了非线性，强耦合性条件下的构形优化。

[1] Carly Rae Jepsen. Modular Reconfigurable Robots.Transaction of Welfares Robotics Systems,Seoul,Korea,Oct.2000.5.

[2] 赵卫东.机器人学[M].北京理工大学出版社.2004.

[3] Jennifer Lopez.Research on the Reconfigurable Robot.PhD Thesis. Stanford University.1998.

[4] David Tao.A New Modular in Reconfigurable Robot.Transaction of the IEEE on Robotics, November 2003.