相控阵天线幅相控制仿真

张晓青，贾豫东，周哲海，曹文娟

(北京信息科技大学 仪器科学与光电工程学院，北京 100192)

相控阵天线(Phased Array Antenna，PAA)是一种先进的天线系统，目前已逐渐应用于各种战术雷达，例如搜索、引导、火控及制导雷达［1］。一些民用雷达，例如空中交通管制系统中的微波着陆雷达、气象雷达等，也开始采用相控阵天线技术。近年来，在传统的相控阵天线系统中引入光学技术，形成新的光控相控阵天线(Optically Controlled Phased Array Antenna，OCPAA)，是目前雷达和通信领域的研究热点。相控阵雷达天线波束的扫描由计算机控制，不存在机械惯性，扫描速度快，方向变换灵活，易于实现低副瓣和波束赋形所需的精密相位和幅度控制。相控阵天线的仿真是一个重要而复杂的过程，方向性函数及其方向图是相控阵天线重要的特性参数，对于天线的优化设计和性能评估有重要意义［2］。由于离散傅里叶逆变换(Inverse Discrete Fourier Transform，IDFT)存在快速算法，即快速傅里叶逆变换(Inverse Fast Fourier Transform，IFFT)，且在MATLAB 中有直接调用的库函数，因此在方向图的计算中使用IFFT 非常方便，提高了多阵列单元方向图函数的运算速度，利于天线的工程设计［3-5］。

本文基于等距线阵方向图与离散傅立叶逆变换的相似性，利用MATLAB 对一维线阵天线的幅相控制过程进行了深入的研究和数值模拟。

1 一维相控阵天线的IDFT 模型

1.1 一维相控阵天线的方向图函数

相控阵天线通过控制阵列辐射单元的馈电幅值和相位来改变方向图形状。微处理器接收到包含通信方向的控制信息后，计算出各个移相器的相移量，然后通过天线控制器来控制馈电网络完成移相过程。通过调整移相器的相移量就可使天线阵波束的最大指向做相应的变化，从而实现波束扫描和跟踪。组成相控阵天线的单个天线单元产生的电磁场在观察点的相位差随方向而变化，合成场在一些方向增强，另一些方向减弱，因而可以得到不同于单个天线单元的方向特性。假设每个阵元为无方向性的点辐射源，各移相器的相移量分别为0、φ、2φ、…、(M-1)φ，即相邻阵元激励电流之间的相位差为φ，典型的一维线性相控阵天线结构如图1 所示。

图1 典型的一维线性相控阵天线结构

若图1 中各阵列单元馈线输入端的激励电流信号幅值为I(k)，且移相器的相移量逐渐递增或递减。若第1 个单元的电流为I0=I(0)ejΨ0，则第k 个单元的电流可表示为Ik=I(k)ejΨk=I(k)ejkφ，则相控阵天线的幅度方向性函数可以描述为级数求和的形式，表示为

1.2 方向图函数与IDFT 的相似性

离散傅立叶变换及逆变换的具体定义如下:设x(n)为N点有限长序列，定义其DFT 为式(2)，定义其离散傅立叶逆变换(IDFT)为式(3)，即

比较式(3)和式(1)，可知等式右边仅相差一个比例常数。对于大型相控阵天线，直接根据公式按级数求和计算相控阵天线方向图的方法计算速度慢、效率低，不能适应工程设计过程中大量仿真计算需求。由于IDFT 的具体表达形式和方向图函数的表达形式相似，可以借助于IDFT 及其快速傅里叶逆变换IFFT 算法来进行相控阵天线方向图的计算［6］。Matlab 中有现成的一维IFFT 函数，为FFT 的计算带来了很大的方便。

为了保持方向图曲线的完整对称性，对式(1)中的φ 增加一个取值点，即定义N+1 个取值点，即

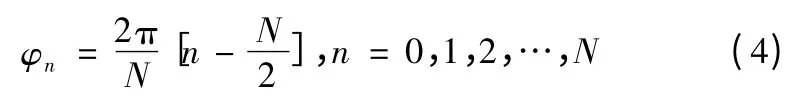
显然，有-π≤φn≤π。对这N+1 个取值点，有

考虑到傅立叶逆变换中存在常数因子，在式(5)中添加常数因子1/N，即

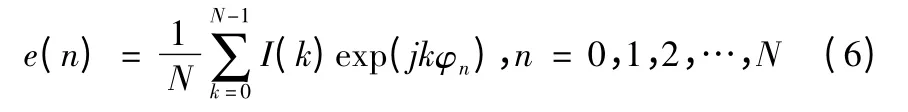
式(6)就是一维相控阵天线方向图函数的IDFT 数学模型。

定义x 轴(即e 轴)负方向的扫描角为负，正方向的扫描角为正。由线阵模型可知，可见空间(或称实空间)内的扫描角θ∈［-π/2，π/2］，因此(∈［-2πd/λ，2πd/λ］。当N 足够大时，e(n)序列可以精确反映线阵方向图特性。

当实际扫描角为θs时，相邻阵元相位差为

方向图函数表达式变化为

则相控阵天线扫描方向图函数的IDFT 模型转变为

2 相控阵天线方向图IFFT 算法

应用IFFT 计算相控阵天线扫描方向图的具体算法如下:

(1)令I(k)=I(k)exp(-jk(s)，k=0，1，2，…，M;

(2)I(k)补零处理。相控阵天线往往具有多个阵列单元，为了确保应用IFFT 计算方向图的正确性，N 应满足N≥M ＞1，且N 为偶数。当N ＞M 时，对I(k)补零处理，即令I(k)=0 (M≤k≤N-1)，而当N=M 时，I(k)不作处理。

(3)IFFT 运算。对复序列I(k)进行离散傅立叶逆变换，即

所得x(n)为N 维向量，即x(n)= {x(0)，x(1)，…，x(N-1)}。

(4)x(n)左右互换。将向量x(n)左右各N /2 个点互换，并考虑序列x(n)具有周期性，得

(5)x'(n)补点。在序列x'(n)后面补上一点x(N/2)，可得N+1 点序列x″(n)如下:

(6)令x″(n)= e(n)。

(7)作图绘出e(n)。

经过上述算法步骤得到的e(n)图形即为相控阵天线扫描方向图。

3 相控阵天线幅相控制仿真

3.1 精确移相的方向图

以M=16 元等距线阵为例，取d =0.5λ，I(k)=1，信号频率为1 GHz，初始角度为法线方向(φ =0°)，方向角θs∈(-π/2，π/2)，I(k)=Iejφ为天线单元的电参数，决定方向图的最大指向，变化天线单元的移相角，观察其方向图的相应变化。

设天线扫描角为θs=15°，则对应的φsn=kφs=-k15°，k=0，1，2，…，15，设扫描角为θs=-15°时，对应的φsn=-kφs=k15°，k=0，1，2，…，15，仿真结果如图2 所示。仿真时取N=1 024，根据IFFT 算法原理可知，IFFT 的点数越多，所得到的方向图越精确。

从图2 可以看出，方向图的最大指向相对于初始移相角为0°时，向左右各平移了15°，主瓣略有变宽，旁瓣位置转移，峰值无明显变化。

3.2 非精确移相的方向图

(1)均匀相位误差。每个天线单元在线性扫描时都有或多或少的误差存在［7］。取固定增长小角度作为扫描角的移相误差，仿真结果如图3 所示，其中，k =0，1，2，…，15。在图3(a)中，方向图的最大指向相对于移相角为0°时，向左平移了15.52°，主瓣略变宽，旁瓣位置转移，峰值无明显变化;在图3(b)中，方向图的最大指向相对于移相角为0°时，向左平移了14.48°，主瓣略变宽，旁瓣位置转移，峰值无明显变化。

图2 扫描角为0°及±15°的方向图

图3 有均匀移相误差的方向图

(2)不均匀相位误差。当φsn=k15° +随机数，k =0，1，2，…，15 时的仿真结果如图4 所示。在图4(a)、图4(b)中，方向图的最大指向相对于相角为φ 时，向左平移了15°左右，分别为14.93°和15.08°，主瓣略变宽，旁瓣位置转移，峰值无明显变化。此时的扫描角误差小于均匀误差情况。

3.3 大角度移相的方向图

应用前面的FFT 方向图算法，对一维线性相控阵天线的大角度移相扫描的情况进行仿真，结果如图5 所示。在θs=±60°时，扫描方向角定位准确，波束主瓣变宽，旁瓣位置转移，主瓣峰值无明显变化;在θs= ±68°时，扫描方向角定位准确，波束主瓣能量泄露严重，开始出现栅瓣［8］，主瓣峰值并无明显变化。

3.4 窗函数幅相控制的方向图

为了防止各种杂波干扰、抑制从天线旁瓣进入的有源干扰，要求相控阵天线的旁瓣电平要尽可能低。在前面的仿真中，令I(k)=1，即采用了矩形窗(boxcar)对I(k)进行了调制，作为发射电流信号幅值的加权方式［9］，仿真结果可参见图2，主瓣窄，旁瓣衰减速度低，幅值识别精度低。这是因为均匀直线阵相当于被矩形窗函数截断，信号的截断产生了能量泄漏，可以通过选择不同的窗函数，对阵元辐射电流的幅值加以处理，对它们的影响进行抑制，从而改善天线图的形状，减小旁瓣，改善天线的辐射能力，仿真结果如图6 所示。

图4 有不均匀相位误差的方向图

图5 大角度移相的方向图

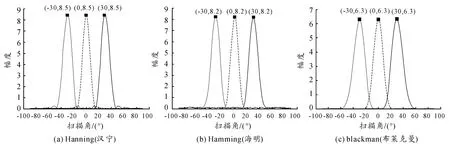
图6 窗函数幅相控制的方向图

从图6 可以看出，汉宁窗幅相控制的方向图主瓣加宽并降低、旁瓣衰减速度快，可减小泄露;海明窗与汉宁窗都是余弦窗，只是加权系数不同，海明窗加权的系数能使旁瓣达到更小，但其旁瓣衰减速度慢;布莱克曼窗控制的方向图主瓣宽、旁瓣小、幅值识别精度较高。

若阵元间距d≥1.1λ 时，旁瓣中有远离主瓣的强干扰分量，应选择旁瓣衰减速度较快的汉宁窗函数实行幅相控制;如果阵元间距d ＞0.3λ 时，强干扰频率分量紧邻主瓣，应选择旁瓣峰值较小的海明窗函数;如果阵元间距d ＜0.3λ 时，旁瓣较大，则用宽主瓣、旁瓣小的布莱克曼窗函数进行幅相控制。

4 结论

本文在相控阵天线方向图函数与离散傅里叶逆变换对应的数学模型基础上，应用Matlab 对发射电流幅相控制的方向图进行了仿真。实验结果表明:采用IFFT 算法计算相控阵天线方向图，方便快捷，给工程设计带来很大的便利;IFFT的点数越多，所得到的方向图越精确。由于目前计算机运行速度很快，即使点数取得很大对运算速度影响也很小;当各个阵列单元的移相误差较小时，会造成扫描角的偏离误差，以及旁瓣形状和位置的改变，不影响主瓣峰值的大小;在大角度扫描时，方向图出现栅瓣，主瓣展宽，探测精确度降低;根据窗函数对发射电流的不同加权效果，可以获得低旁瓣的方向图，从而改善天线探测能力。上述相控阵天线方向图幅相控制的扫描规律可为进一步分析和设计相控阵天线的结构、移相器以及幅度加权等方面提供理论依据。

［1］张光义.相控阵雷达系统［M］.北京:国防工业出版社，1994:36-44.

［2］陈志杰，李永祯，戴幻尧，代大海.相控阵天线方向图的建模与实时仿真方法［J］.计算机仿真，2011，28(3):31-35.

［3］刘俊群.平面天线阵方向图的FFT 算法简析［J］.测控技术，2008，34(9):1-3.

［4］王曼珠，张喆民，崔红跃.MATLAB 在天线方向图中的应用与研究［J］.电气电子教学学报，2004，26(4):24-27.

［5］张立东.MATLAB 语言在天线设计中的运用［J］.制导与引信，2004，25(1):34-37.

［6］李建新，徐慧，胡明春，邵江达.基于FFT 的阵列方向图快速计算［J］.微波学报，2007，23(1):10-15.

［7］王颍辉，匡勇.相控阵天线指向误差分析［J］.中国电子科学研究院学报，2011，6(4):340-346.

［8］常硕，王德功，李圭源.相控阵雷达天线方向图仿真研究［J］.中国雷达，2008(1):35-37.

［9］张社欣，李文臣，郭新海.密度加权相控阵天线方向图仿真［J］.舰船电子对抗，2006，29(4):73-76.