基于超声TOFD法直通波幅度分布的近表面缺陷检测

陈振华，胡怀辉，卢 超

（南昌航空大学 无损检测教育部重点实验室，南昌 330063）

超声衍射回波法（Time of Flight Diffraction）技术具有可靠性好、检出率高、定量准确、效率高、成本低［1－2］等优点，越来越多地应用于无损检测领域。然而，常规超声TOFD检测技术也有其局限性，表面检测盲区问题即是超声TOFD检测方法需解决的问题之一。

降低检测盲区的手段主要有检测信号分析以及优化检测方法延长衍射波传播路径。迟大钊、陈伟［3－6］等人提出了一种基于图像能量分布的方法，通过数字图像处理及信号分析，提取了混叠的缺陷端衍射波信号，提高了近表面缺陷的识别能力，但该方法对缺陷信号的提取受待处理图像的成像质量影响很大，存在侧向波抑制不完全或损伤缺陷信号的问题。张锐、陈天璐［7－11］等人通过优化检测方法增大衍射波的传播声程，提高对近表面缺陷的检测能力。但由于衍射波声程的增大，端部衍射衰减较大，且信号中声波成分更加复杂，难于分析，造成对较小的近表面缺陷检测困难。

笔者主要对近表面缺陷检测的直通波信号幅度分布进行试验，针对直通波时域范围内选取多个关键点，通过这些关键点在不同近表面缺陷的幅值变化，发现了与直通波重叠的端部衍射波。基于直通波幅度分布提出了检测特征值，根据该特征值分布能够检测近表面缺陷并估计其深度，提高对近表面缺陷的检测能力。

1 试块制作

试验制备了用于近表面缺陷检测的试块。试块材质为 A7N01－T4铝合金，尺寸为320mm×200mm×20mm。在垂直于铝合金板的板面制备了深度不同的浅孔，直径均为φ1mm，孔深分别为1，2，3，5，8，10mm，各浅孔间距40mm，如图1所示。

图1 试块结构尺寸

2 试验方法

检测中采用斜角为60度，中心频率为5MHz的超声TOFD检测专用探头。检测系统的最大采样率为60MHz。两探头以被检孔为中心对称放置，探头间距设为5mm，如图2所示。试验对近表面各浅孔进行检测，提取检测波形。

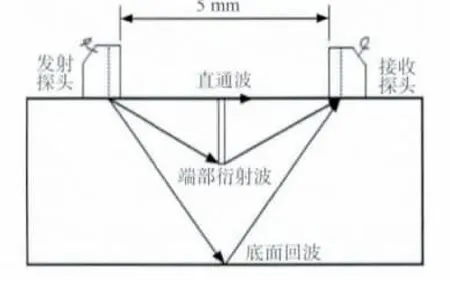
图2 探头布置示意

人工缺陷的开口浅孔对板面破坏导致直通波衰减，图3为检测直径φ1mm、深10mm孔与表面完整时的直通波信号。10mm深孔的检测直通波不受端部衍射波的影响而仅由表面的破坏引起，因此为更准确地描述近表面缺陷尖端衍射对直通波幅度的影响，同时又不引入表面破坏的干扰，试验中采用直径φ1mm、深度10mm深孔的检测直通波作为无近表面缺陷的检测信号。

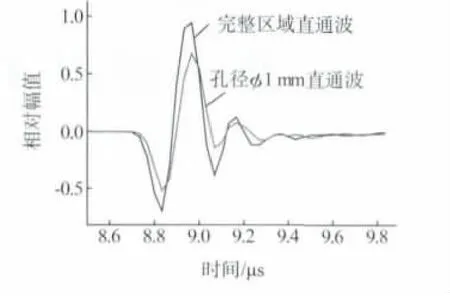
图3 表面破坏对直通波波幅的影响

图4 为各浅孔的超声TOFD检测直通波信号，其中虚线为10mm深孔的检测信号（即无近表面缺陷时的直通波信号）。图4显示，孔深为1，2mm时几乎看不到端部衍射波，孔深3mm时开始出现较明显的衍射波形，当孔深增大到5mm时，能清晰地看到衍射波信号。

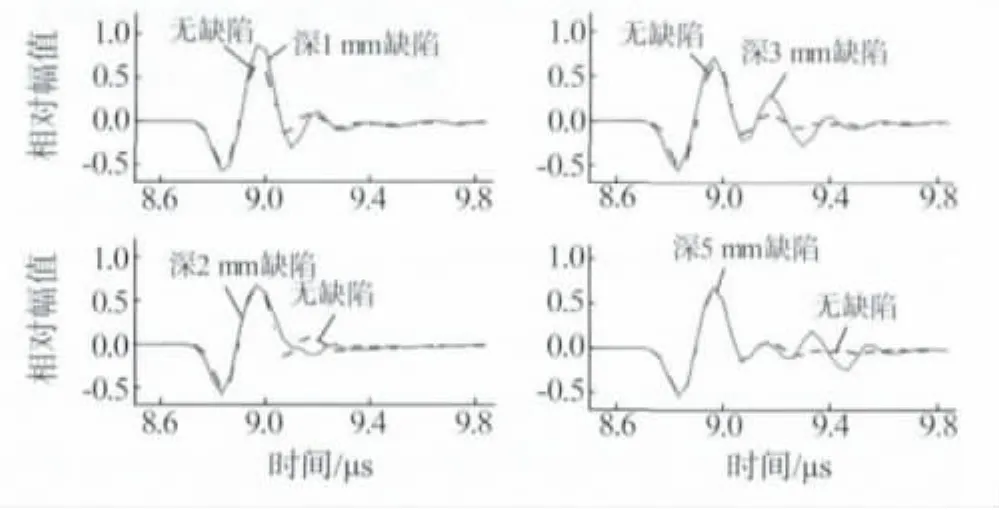
图4 近表面缺陷波形与无近表面缺陷波形对比

图4 显示的试验结果与理论一致。式（1）是衍射波与直通波时间差的理论公式，可见随着缺陷深度的增大，衍射波与直通波的时间差值Δt逐渐增大，即端部衍射逐渐移出直通波并完全分离出来。

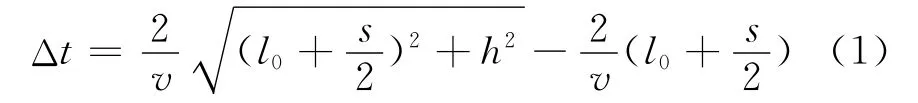
式中：s为两探头间的距离；h为缺陷深度；v为声速；l0为探头前沿长度。

此外，由图4可知，直通波幅值分布随着孔深的增大也发生了变化。直通波幅度的变化与浅孔深度存在一定联系。因此探讨直通波幅值分布随孔深的变化规律可为近表面缺陷检测提供依据。

3 近表面缺陷尖端衍射波对直通波幅度分布的影响

在直通波时域范围内选取多个关键点，通过各关键点的幅值变化，研究直通波与浅孔端部衍射波的相互作用，各关键点编号为A～E，如图5（a）所示。1～5mm浅孔以及无近表面缺陷时直通波各个参考点的幅值变化数据如图5（b）所示。与无近表面缺陷直通波信号相比，1mm浅孔的A点幅度变化最大，其余关键点幅度基本不变；2mm浅孔的B，C点幅度的变化较大；3mm浅孔的C，D点幅度变化最大；5mm浅孔的E点幅度变化最大，其余关键点基本恢复原幅值。通过图5（b）的变化趋势可推断随孔深的增大，其端部衍射波对直通波幅度的影响在时域上逐渐右移（即由A向E移动）。

图5 直通波各关键点幅值变化关系

进一步分析直通波幅度分布变化的原因可知，近表面缺陷端部衍射波不仅存在且与直通波相互叠加。按图5（b）的变化趋势可模拟不同深度近表面缺陷端部衍射波对直通波的影响，如图6所示。图6（a）显示1mm浅孔的端部衍射波与直通波相互叠加，造成A点幅度增大；图6（b）显示当孔深为2mm时，尖端衍射波向右移动一定距离，衍射波仍在直通波脉冲宽度内并与之叠加，使得B，C点处幅度显著降低；图6（c）显示浅孔深3mm时，尖端衍射波继续远离直通波，C，D处叠加增强；图6（d）显示当浅孔深5mm时，衍射波信号与直通波信号分离开来。因此可见，图6中所模拟的衍射波特征与图5（b）中由衍射波引起的各关键点幅值变化情况一致。

图6 各不同深度缺陷模拟衍射波相对直通波的位置变化

在相同试验条件下采集8，10mm孔深的端部衍射波波形，如图7所示。图7是试验测得的衍射波波形特征。可见，衍射波的相位变化与入射界面两侧介质有关，与孔深度无关。因此从衍射波相位及幅值分布看，图6中模拟的端部衍射波与真实衍射波具有较好的一致性。

图7 各不同深度缺陷所检测的波形

此外，根据式（1）可计算出各浅孔端部衍射波位置与直通波的时间差值。随孔深的增大，直通波与尖端衍射波的叠加状态不断发生改变，直到尖端衍射波完全与直通波分离。图8的计算值与图6的衍射波位置基本一致，进一步证明了浅孔尖端衍射波的存在及其与直通波的叠加规律。

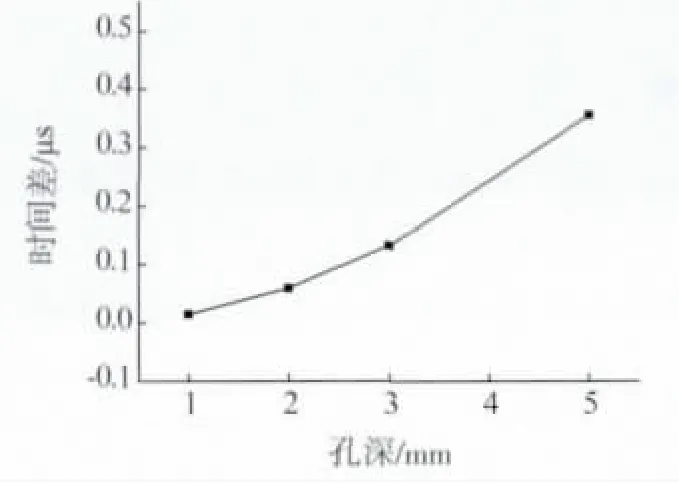
图8 各浅孔的衍射波与直通波起点的时间差

通过以上分析可知，超声TOFD检测近表面缺陷时，其直通波的幅值变化包含着大量的近表面缺陷信息，通过直通波幅度的分布特征可以对近表面缺陷进行检测。为了能够更直观地检测近表面缺陷，试验基于直通波幅度分布定义了检测特征值，如式（2）。

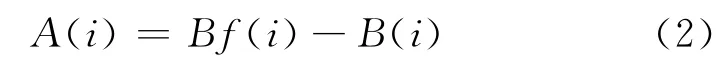
式中：A（i）为检测特征值；Bf（i）为近表面缺陷直通波幅值分布；B（i）为无近表面缺陷时的直通波分布。

依据试验数据可得到各浅孔的检测特征分布如图9所示。各类缺陷情况下，其特征值分布具有明显差异，依据该特征分布能够对近表面缺陷进行检测并估计缺陷深度。

图9 近表面缺陷超声TOFD直通波幅度检测特征值分布

4 结语

近表面缺陷的端部衍射波与直通波相互叠加，影响直通波的幅度分布，直通波幅度分布中包含大量的缺陷信息。基于直通波幅度分布提出了近表面缺陷的检测特征值。通过该特征值的分布可以检测近表面缺陷并估计缺陷的位置，可提高超声TOFD技术对近表面缺陷的检测能力。基于直通波分布所检测特征值容易受到表面状态，如污染、腐蚀、划痕的影响，因此文中所述方法对被检件的表面状态要求较高。

［1］伊新.TOFD检测技术基本原理及其应用探讨［J］.石油化工应用，2008，27（3）：29－31.

［2］Gang Tie，Chi Dazhao.Novel approach to the enhancement of ultrasonic TOFD B－scan image for the measurement of weld crack［J］.Science and Technology of Welding and Joining，2007 ，12（1）：87－93.

［3］迟大钊.基于超声TOFD法的焊缝缺陷表征研究［D］.哈尔滨：哈尔滨工业大学，2007：52－71.

［4］陈伟，詹红庆，杨贵德，等.基于直通波抑制的超声TOFD图像缺陷检测新方法［J］.无损检测，2010，32（6）：402－405.

［5］Atkinson I.High accuracy defect sizing for CRDM penetration adapters using the ultrasonic TOFD technique［J］.Insight：Non– Destructive Testing and Condition Monitoring，1995，37（3）：175－178.

［6］Chi D Z，Gang T，Gao S S.Background removal and weld defect detection based on energy distribution of image［J］.China Welding，2007，16（1）：14－18.

［7］张 锐，万明习，Cao W W.超声衍射—回波渡越时间方法焊缝裂纹原位定量无损估计［J］.机械工程学报，2000，36（5）：54－57.

［8］陈天璐，阙沛文.基于超声衍射反射回波渡越时间的缺陷识别技术［J］.化工自动化及仪表，2006，33（4）：50－52.

［9］Baskaran G，Balasubramaniam K，Rao C L.Shearwave time of flight diffraction （S－TOFD）technique［J］.NDT＆E International，2006，39（6）：458－467.

［10］孙忠波，齐向前，张平.TOFD检测中采用二次波评定进扫查面缺陷尺寸的方法［J］.无损检测，2009，31（9）：694－696.

［11］迟大钊，刚铁，姚英学，等.一种基于超声TOFD法的近表面缺陷检测模式［J］.焊接学报，2011，32（2）：25－28.