高速压力机重心位置对机身固有频率的影响研究

施立军，何彦忠，陈文家

（1.扬州大学 机械工程学院，江苏 扬州 225127；2.江苏扬力集团 精密机床研究所，江苏 扬州 225127）

1 引言

随着压力机工作速度的提高，其动态性能和振动问题的分析愈来愈重要。单纯的静态设计和经验设计已不能完全满足工程实际的要求。在进行结构设计时，必须考虑到各种动态因素的影响，对结构进行详细的动力分析，以达到抗振、安全、可靠的目的。工程结构要具有与使用环境相适应的动力学特性，否则结构模态与激励频率耦合会使机床产生共振，严重时会使整个机床发生抖振，使机床噪声过大，局部产生疲劳破坏等。为此，本文提出了高速压力机床身模态分析评价方案：①压力机床身的弹性模态频率应避开电动机经常工作频率；②压力机床身的低阶固有频率应避开压力机的工作频率；③对压力机工作精度影响最大的方向振幅较小、基频较高、在规定频率范围内出现的振型数目较少则压力机的动态性能较好。根据模态评价方案，结合压力机在使用环境下的实际激振频率，通过结构设计使床身各阶模态频率尽可能远离这些实际激振频率。在大量的床身结构设计与模态分析过程中发现，床身重心位置是影响机身固有频率和固有振型的关键因素，因此对重心位置在模态分析结果中固有频率、振型的影响规律研究是非常有必要的。

2 重心位置与机身固有频率影响关系理论推导

2.1 机身力学模型创建

假设机身上安装的零件质量分布比较集中，可以简化成单自由度质量块，且机身各截面形状变化不大，基本上有统一的截面惯性矩，每一部分都可看作通过截面形心的一根梁，且变形在弹性变形之内。

图1a 为JE21S-25 型深喉颈压力机机身结构简图，将其简化成单自由度振动系统，其力学模型如图1b 所示。下面用Rayleigh 法推算其机身固有频率与重心偏移的关系。

2.2 机身固有频率计算

图1b 中m 为安装于机身上的各部分零件的质量总和；m1、m2、m3分别为机身上 l1、l2、l3部分的质量，单位 kg；J1、J2、J3分别为 l1、l2、l3部分的截面惯性矩，单位 m4；l1、l2、l3单位 m，且 l1=l2。

设振动中m 的位移之和为y（t），当x=l1时，m的静态垂直位移和fst为：

系统的弹性常数K 为：

设m 的运动按正弦规律变化，即：

系统的最大势能为：

系统的最大动能为：

由能量守恒定律有Vmax=Wmax，得机身固有频率f为：

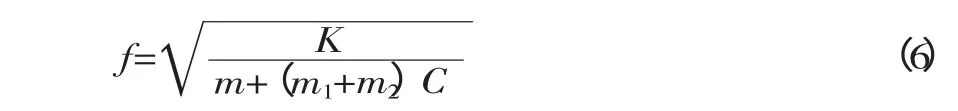
其中：

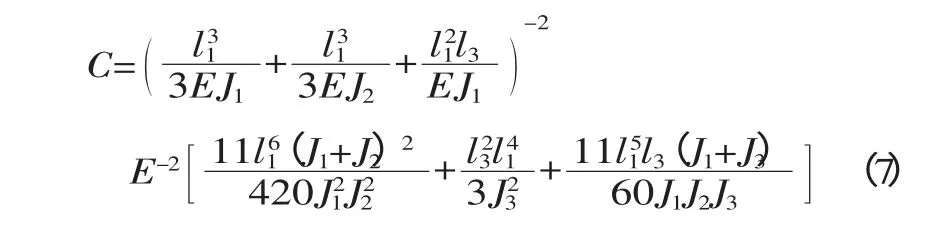
式中：K——弹性常数；

f——压力机机身的固有频率；

M——安装于机身上的零部件质量总和；

m1、m2——机身上长度分别为 l1、l2部分的质量；

E——机身材料的弹性模量，钢板焊接机身E=2.1×1011N/m2。

设计时，通过重心位置确定l1、l2部分的质量m1、m2及截面惯性矩后带入公式（6）就能得出固有频率。通过对机身结构数据的初步计算整理，结果列入表1。

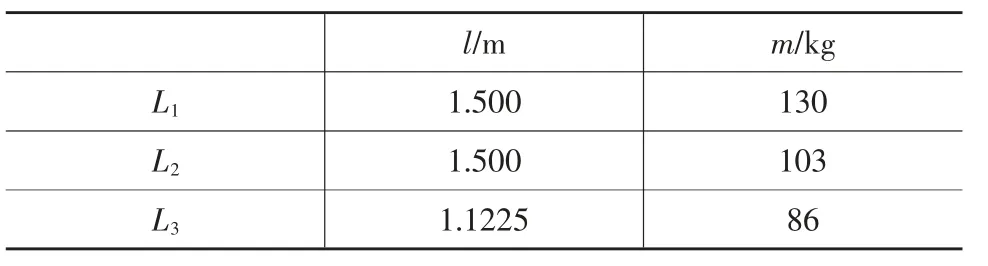
表1 机身结构数据

另外，机身上零件的总质量m=2841kg，将l1、l2、l3的数值带入公式（7）继续推导得：

众所周知，当截面不变的情况下，重心偏移量增大时，会导致截面惯性矩 J1、J2、J3增大，而由公式（8）可以看出，当界面惯性矩 J1、J2、J3增大时，固有频率C 减小。

结论：当其他因素一定时，机身重心的偏移量增大导致其固有频率减小。

3 有限元法验证分析

3.1 有限元计算模型创建

本文以开式深喉250kN 压力机为例，电机转速为1250rpm，则电机的工作频率为20.83Hz，压力机滑块行程为60mm，滑块行程次数为150spm，故压力机的工作频率2.5Hz，实际压力机床身的各阶固有频率要远大于压力机的工作频率，因此对于该机身的动态性能的优化即是尽量提高频率，使其进一步远离压力机的工作频率以及避开电机工作的频率。创建三种不同质心位置统一规格型号的床身模型进行计算分析。三种机身的主视工程图及质量属性、材料属性等数据见表2。

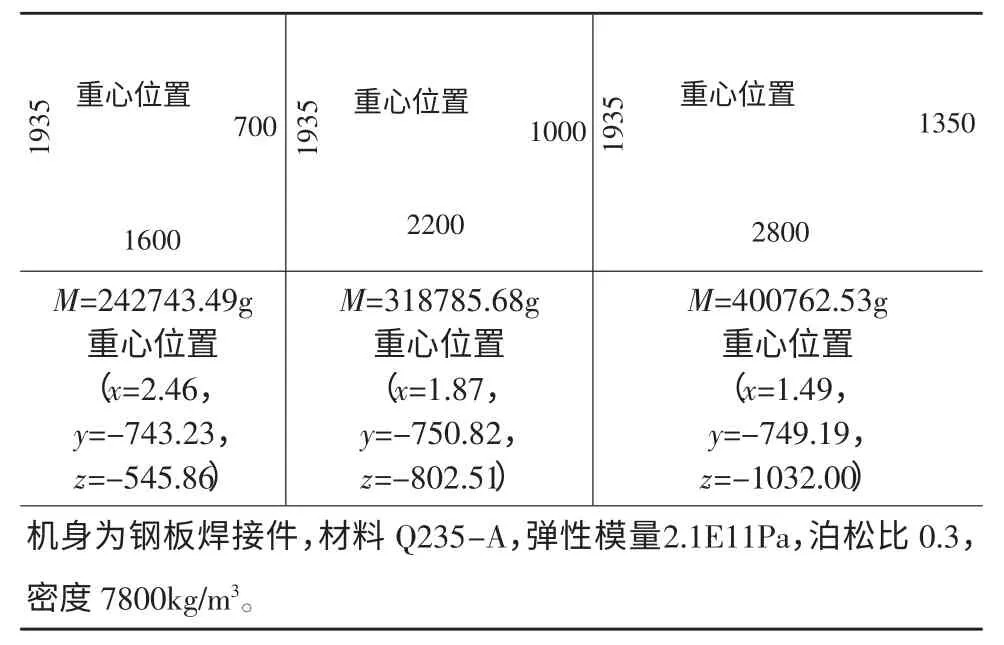
表2 三种机身有关数据

3.2 模态计算结果与对比分析

对有限元模型进行模态分析，分别得出三个机身前两阶固有频率（表3）及前两阶固有振型（图2～图7）并采集三个机身同一侧导轨处的变形曲线图（图8～图 10）。

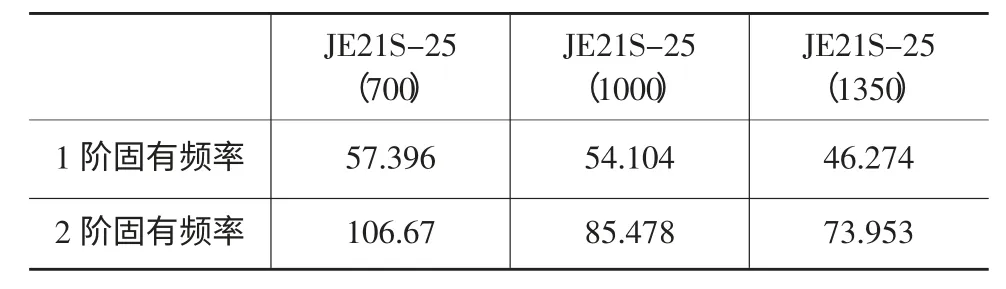
表3 三种机身前两阶固有频率

由以上振型图及导轨处变形曲线图可以看出，由于地脚螺栓的固定作用，工作台基本上没有振动变形，振幅从工作台向机身顶部逐渐增大。工作台的位移相对较小，最大位移发生在工作台正上方的机身顶部及机身背部的倒角处，而工作台正上方的机身变形将直接影响安装于其上的滑块的运动方向及其与工作台面的垂直度，从而降低模具及工件的加工精度。同时，振动还将引起螺栓的拉伸和弯曲变形，久而久之，将引起固定失效，从而带来安全隐患并将给企业带来直接的经济损失。

根据有限元分析及对比，实验结果完全符合上文推导得出的规律，实例验证了机身重心偏移量增大导致其固有频率减小。

4 机身设计实例验证

4.1 机身的建模与有限元分析验证

由于质量也是影响机身固有频率的因素，所以不同种机身质量不同，有可能影响到规律的准确性，所以取一种机身，对其机身进行修改，使其满足质量相等重心位置不同的前提条件，然后对重心偏移量与固有频率的关系规律进行验证。

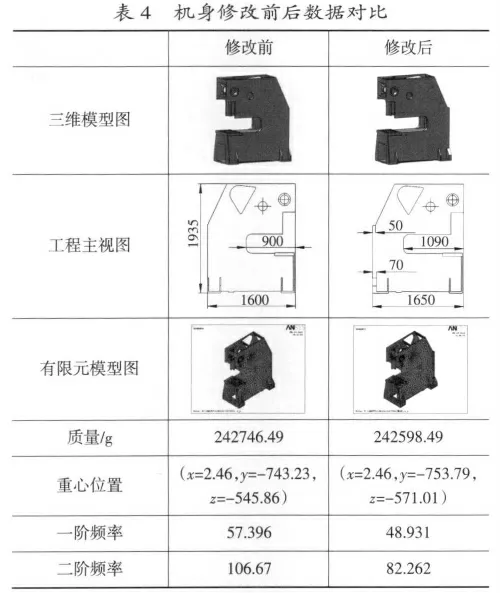
首先用SolidWorks 三维建模软件对JE21S-25（700）机身做如下修改：将机身背部加厚50mm，吼口加深190mm，以得到机身修改前后质量相同而重心偏移量不同的前提，然后对机身进行网格划分得到有限元模型，进而进行求解运算，得出机身修改前后的前两阶固有频率，通过分析验证机身重心偏移位置对其固有频率的影响规律的正确性。机身修改前后图形及数据对比见表4。

由表2 可以看出，机身模型修改前后，质量几乎没有改变，可以认为质量相等，而由重心位置坐标对比可以看出，修改后的机身重心偏移量更大。因此通过ANSYS 有限元分析计算得出，在质量相同的情况下，机身重心偏移量越大，其固有频率越小，更有力地证明了上文得出的结论的正确性。

?

4.2 小结

由于压力机机身的弹性模态频率应避开电动机经常工作频率且低阶固有频率应避开压力机的工作频率，使其基频较高，在规定频率范围内出现的振型数目较少，并且结合压力机在使用环境下的实际激振频率，通过结构设计使床身各阶模态频率尽可能远离这些实际激振频率。所以利用我们得出的规律，压力机机身设计时，在满足其他设计要求的同时，应该尽量减小机身的重心偏移量，以达到增加其低阶固有频率的目的，有效避免共振的可能性，并使其动态性能更加优越。

5 总结

（1）用Rayleigh 法针对压力机重心偏移量对压力机机身固有频率的影响关系进行了理论公式的推导，并总结了前者影响后者的基本规律。

（2）用ANSYS 有限元法证明了压力机机身重心偏移量是影响其固有频率的重要因素之一，并通过两次有限元计算对比分析，验证了二者之间的规律关系。

（3）提出了在满足基本设计要求下进一步避免压力机引起共振的理论方法，为压力机的设计研究工作提供了重要的理论依据。

[1]梁 磊，赵迎祥，韩玉强，等.用瑞利法计算数控回转头压力机机身固有频率[J].机床与液压，2008，（7）：62-64.

[2]丁 旺，丁学武，冯丙波.基于ANSYS 的高速压力机模态分析[J].苏州科技学院学报（工程技术版），2011，（1）：81-83.

[3]张 鹏，韩世超，王兆娜.JG21-250A 型压力机机身的有限元分析及优化设计[J].机械，2009，（12）：32-34.

[4]赵兰磊，何彦忠，陈文家，等.基于ANSYS 与COSMOSXpress 对闭式压力机机身的有限元分析及优化 [J].机械工程师，2011，（12）：101-104.

[5]董宏斌，何灿焜，张庆飞.数控精密成形压力机机身结构有限元分析[J].锻压装备与制造技术，2005，40（6）：30-32.

[6]张义民.机械振动[M].北京：清华大学出版社，2007.

[7]刘鸿文.材料力学[M].北京：人民教育出版社，1981.

[8]张贵成，阮卫平，符起贤.闭式单点压力机机身的有限元分析[J].锻压装备与制造技术，2009，44（1）：22-23.

[9]张献图，韩运侠，戴彦杰.求固有频率的一种简易方法[J].洛阳师专学报，1997，（2）：60-62.

[10]张益锋，夏 亮，詹俊勇.J75G-200 型闭式高速精密压力机机身分析[J].安徽水利水电职业技术学院学报，2011，（1）：8-10.