双正态总体均值的置信区间估计及MATLAB实现*

张林泉

(广东女子职业技术学院，广东广州511450)

区间估计(interval estimation)是包括估计量在内(有时是以估计量为中心)的一个区间;该区间被认为很可能包含总体参数.重复抽取大量(样本量相同的)样本时，产生的大量类似区间中有些会覆盖真正的p，而有些不会;但其中大约有95%会覆盖真正的总体比例.这样得到的区间被称为总体比例 p的置信度(confidence level)为95%的置信区间(confidence interval).在实际问题中，不仅需要求出参数的近似值，还要大致估计这个近似值的精确度和可靠性［1］.两个总体均值的置信区间是由两个样本均值之差加减估计误差.得到的估计误差由两部分组成:一是点估计量的标准误差，它取决于样本统计量的抽样分布.二是估计时所要求的置信水平为1－α时，统计量分布两侧面积为α的分位数值，取决于事先所要求的可靠程度两个总体均值之差在置信水平下的置信区间可一般性地表达为分位数值的标准误差.本文就如何利用样本函数，讨论未知参数的置信区间，结合实例进行分析，并给出在MATLAB平台实现的程序.

1 双正态总体均值之差的区间估计 (、未知，但=)

设两个正态总体 X 与 Y，且 X ～ N(μ1，σ)，Y ～ N(μ2，σ)，(X1，X2，…，Xn1)为来自总体 X 的样本，(Y1，Y2，…，Yn2)为来自总体Y的样本，并且两组样本相互独立，σ、σ未知，但σ=σ.求总体均值之差μ1－μ2的1－α置信区间.

(x1，x2，…，xn1)为总体 X 的一组样本观测数据;(y1，y2，…，yn2)为总体Y的一组样本观测数据.

则由两个总体的抽样分布中的结论可知

对于给定的置信度1－α，由t分布密度曲线关于y轴对称，寻找临界值tα/2(n1+n2－2)使得

当给定α时，查自由度为n1+n2－2的t分布临界值表，可得到临界值 tα/2(n1+n2－2).

得到临界值tα/2(n1+n2－2)后，由不等式

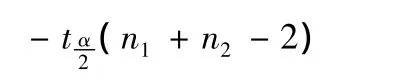
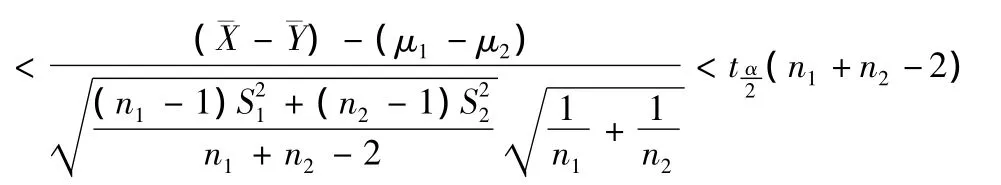
可以推得:

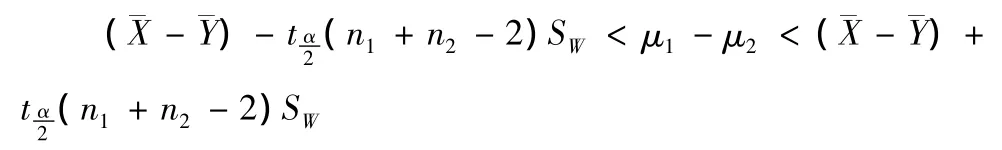
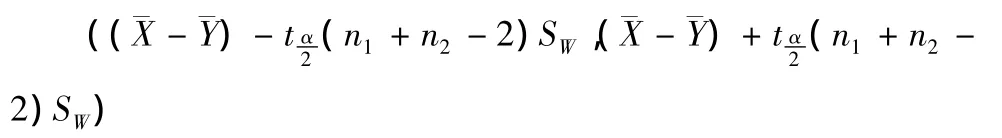
即有(1－α)的可能性判定μ1－μ2落在上述区间内［2］.

例1 为了比较甲、乙两类保险公司中具有高等教育水平的员工比例，从甲类公司中随机抽取8个，测得平均比例，样本标准差分别为，从乙类公司中随机抽取10个，测得平均比例，样本标准差分别为S2=.13178，并且根据长期经验可知，两总体都是正态分布，方差相等，求两总体均值差μ1－μ2的95%的置信区间［3］.

解:由于两类公司各自随机抽取，所以可以认为两组样本独立.又知两总体方差未知但它们相等，选取统计量

根据样本观测数据(x1，x2，…，xn1)、(y1，y2，…，yn2)，计算样本均值的观测值与，样本方差的观测值S1与S2，就可以得到一个具体的关于μ1－μ2的1－α置信区间为:

由题意 α =0.05，n1+n2－2=8+10 －2=16.

查自由度为16的t分布临界值表，可得临界值

结果表明:有95%的把握断定，乙类公司具有高等教育水平员工比例的均值高，平均比例最多比甲类公司多31.033%，最少多9.68%.

2 双正态总体均值之差的区间估计(、未知;n1，n2≥50)

设两个正态总体 X 与 Y，且 X ～ N(μ1，)，Y ～ N(μ2，)，(X1，X2，…，Xn1)为来自总体 X 的样本，(Y1，Y2，…，Yn2)为来自总体Y的样本，并且两组样本相互独立，、未知，求总体均值之差μ1－μ2的1－α置信区间.

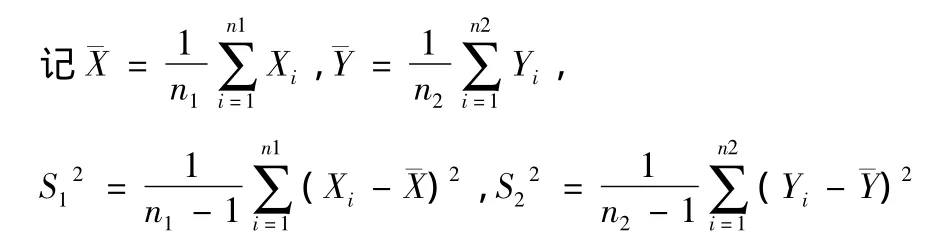
分别是总体X与总体Y的样本均值和样本方差.

设(x1，x2，…，xn1)为总体X的一组样本观测数据;(y1，y2，…，yn2)为总体Y的一组样本观测数据.

当 n1、n2都充分大时(n1≥50，n2≥50)，t分布近似于标准正态分布，即

则由数学期望和方差的性质，有

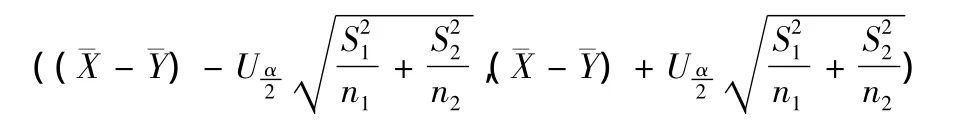
其中Uα/2为临界值，其值可通过查标准正态分布函数数值表得到［2］.

例2 2825本市户口和168外市户口家庭人均住房面积，本市户口的平均面积为21.7258平方米，样本标准差为12.17539;外市户口平均面积为26.7165平方米，样本标准差为18.96748.假设本市户口和外市户口家庭人均住房面积均服从正态分布，μ1表示所有本市户口的平均面积，μ2为所有外市户口的平均面积，求μ1－μ2的95%的置信区间［3］.

解:由于两个总体的方差未知，且n1=2825，n2=168，有统计量

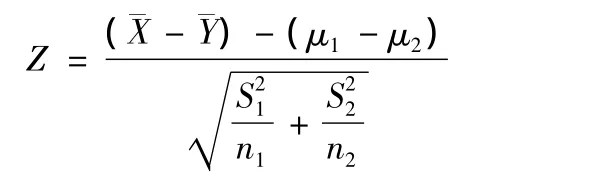
近似服从N(0，1).已知α =0.05，∴ Φ(Uα/2)=1 － α/2

反查标准正态分布函数数值表，得临界值U0.025=1.96.

∴μ1－μ2的95% 的置信区间为:

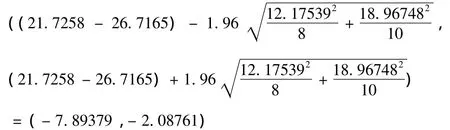
由两总体均值差的95%的置信区间，区间不跨零，可以认为两总体均值存在显著差异，本市户口和外市户口的家庭人均住房面积的平均值存在显著差异.

3 双正态总体均值置信区间的MATLAB实现

在例1中，在命令窗口输入:t=tinv(0.975，16);s=sqrt((7*0.16957^2+9*0.13178^2)/16);

得到结果:{－0.310324，－0.00967568}

在例2中，在命令窗口输入:z=norminv(0.975);

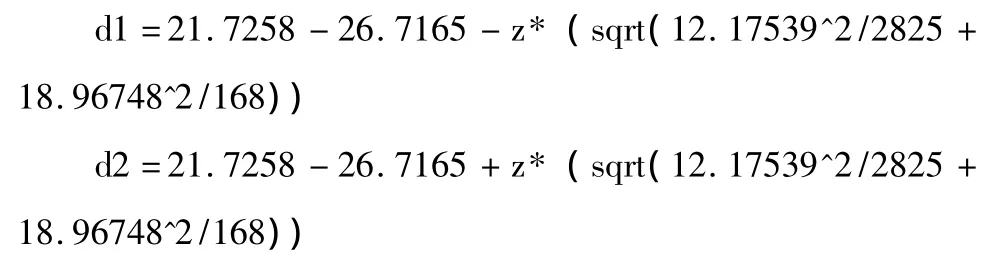
得到结果:{－7.89379，－2.08761}［4］.

4 结语

求置信区间的一般步骤如下:第一，确定样本统计量.用来估计总体参数;第二，选择一个置信水平1－α;第三，找到误差边际，误差边际=临界值*统计量的标准误;第四，指定置信区间，置信区间=样本统计量±误差边际［5］.综上，确定区间估计关键是要寻找一个待估参数θ和估计量T的函数U(T，θ)，且U(T，θ)的分布为已知，不依赖于任何未知参数.而这与总体分布有关，所以，总体分布的形式是否已知，是怎样的类型，至关重要.给定样本，给定置信水平，置信区间也不是唯一的.

［1］吴喜之.统计学:从数据到结论(第三版)［M］.北京:中国统计出版社，2006.

［2］曾五一.统计学简明教程［M］.北京:中国人民大学出版社，2012.

［3］薛微.统计分析与SPSS的应用(第三版)［M］.北京:中国人民大学出版社，2011.

［4］Marchand P，Holland O T.Graphics and GUIs with MATLAB［M］.Florida:CRC Press，2003.

［5］拉森，法伯.基础统计学(第四版)［M］.北京:中国人民大学出版社，2010.