中国资本市场是否存在逐富效应——“高投资低消费”之经济原因探索
张 勋,孙 晨,孙伊满
(北京大学国家发展研究院,北京100871)
一、引 言
中国经济自改革开放以来三十几年的高速增长令世界侧目,对于“中国奇迹”的解释也层出不穷,目前国内比较主流的理论解释有“制度变迁说”、“比较优势说”、“分权说”等,但由于中国的市场经济仍在不断完善之中,加之经济结构转 型方兴未艾,聚焦于市场的理论解释并未引起应有重视。而眼下面临后金融危机时代全球经济再平衡的大背景,有必要从市场的角度重新审视中国经济的症结。
收入分配不平等,消费占GDP比重逐年降低,投资占GDP比例逐年上升,这些问题的存在是否会制约中国经济未来的持续增长是值得深思的主题。而说到底,经济的持续增长离不开资本的可持续累积。换言之,市场中经济行为人对资本的追逐是推动经济不断增长的动力之一①结合中国实际国情,政府投资也占很大比重,但为方便讨论,统一称为经济行为人。。但在标准的新古典模型中,资本累积只是为了满足行为人增加消费的需要,这与现实有不小出入。因为很多高收入个体,对于消费的需求已经达到饱和,不可能超过生理界限,他们仍然拼命工作,继续追逐财富就不能再解释为满足消费,而更可能是为了保持他们现有的社会地位。这种因追求社会地位、权力而追逐资本的动机被马克斯韦伯称为“资本主义精神”。现有文献对资本主义精神的研究应当从财富效应说起。1968年,财富效应便被引入经济行为人的效用函数,讨论经济的最优增长路径[1]。实证上,也有学者证实了对地位和财富的追逐也可能会改变经济主体人的行为[2]。在Robson讨论的基础上,有学者加入了文化效应进行探讨,但对地位的追逐仍然是一个行为主导的重要因素[3]。有学者则是从微观层面,用资本主义精神解释了长期的经济增长和储蓄率变动[4-5]。资本主义精神是经济行为人产生资本偏好的原因,这反过来也会造成资本市场上资产价格的波动[6-7]。
现有文献已经比较完整地建立了逐富效应所代表的资本主义精神的分析框架,但鲜有文献对中国是否存在资本主义精神,若存在它如何影响总体经济做出过探讨。本文认为,随着中国资本市场的日益发展,经济行为人的投资渠道增多,可能愈发显现出追逐财富的偏好。而追逐财富所带来的效用不仅体现在消费上,更多地也体现为拥有更高的社会地位,或是建立更好的社会网络上。为此,本文尝试将经济行为人因追求财富和社会地位而存有的“资本偏好”因素加入效用函数,通过对消费、储蓄以及资产组合选择行为进行分析,由此说明“资本偏好”对中国资本市场上资产价格的波动有重要影响,进而得出“资本偏好”是经济行为人追逐财富的动机之一,从而提供一种解释中国经济增长的新视角。因为一旦确定“资本偏好”的重要作用,对当下中国高投资低消费的成因可以解读为在现有收入分配格局下,经济行为人对社会地位的追求引致的对财富的追逐①当然不能忽略的是现有收入分配中存在的各种问题,如国企垄断,权力寻租,城乡二元化等,但限于本文讨论的主题在此不做具体讨论。。而这一论断一旦成立,则说明中国经济现在的“高投资”是由从市场经济发展阶段内生而来的“资本偏好”引起的。为了检验“资本偏好”假说,我们采用GMM估计方法,利用中国的月度数据进行检验。总体来看,估计的参数值和符号支持“资本偏好”的假说,即证明了中国资本市场存在逐富效应。而与标准的期望效用理论相比,我们的估计考虑了对财富和社会地位的偏好,从而对股票价格的波动有更好的解释。
下文安排如下:第二部分引入衡量逐富效应的偏好模型,由此探讨经济行为人的消费,投资组合问题;第三部分对数据进行统计描述,并通过第二部分所建立的模型对参数进行估计,报告实证结果,对中国的“资本偏好”现象进行检验;第四部分做总结性讨论。
二、理论模型
为了刻画经济行为人因追求社会地位而存有的“资本偏好”,我们采用了Bakshi和Chen的模型框架。Bakshi和Chen主要讨论了美国的资本偏好现象,其结论为美国确实存在着“资本主义精神”。但美国与中国实际国情的不同造成了该模型刻画并不能完全描述中国的现象,因此本文讨论了中国的情形,并对模型和数据进行了一定的修正,以期符合中国的实际情况。
(一)一般均衡模型的框架
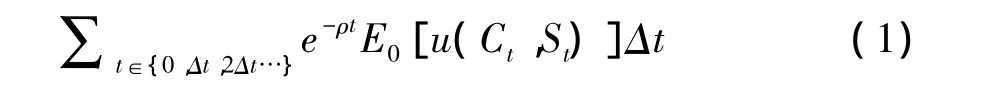
其中效用函数满足uC>0,uS>0,uCC<0,uSS<0,uCS可为任意符号。
相对财富是一个新引进的变量,它受到两个方面的影响。首先是绝对财富Wt,其次是社会阶层Vt,给定绝对财富不变,社会阶层越高,相对财富越低。正式地,我们有如下表达式:

上式满足fW>0,fV<0。
但在考虑中国问题时,我们主要采用的是改革开放后经济发展较成熟的10年作为样本窗口。在这个样本窗口内,国家经济政策导向基本还是围绕让东部先富的政策,社会财富的阶层并没有发生根本性的转变。当然,在2010年后续政策中,我们就必须考虑先富带动后富的阶层变动了。但在此,我们假设社会阶层Vt为常数并不随着时间变化,则引入如下具体效用函数:
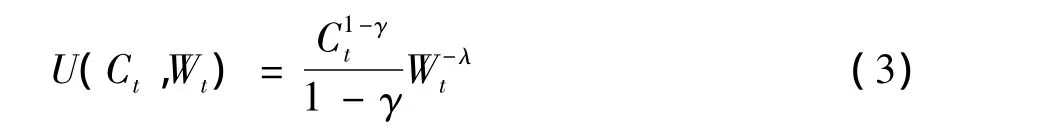
其中若 γ≥1,λ ≥0,否则γ <1,λ <0,|λ|测度的是投资者对社会地位的关注程度。
(二)模型求解
为了求解效用最大化问题,必须引入资产。假设经济体有一种无风险资产和N种风险资产。无风险资产的收益率为恒常值r0,而风险资产在t期的价格表示为Pi,t,假设该价格符合以下的随机漂移过程:
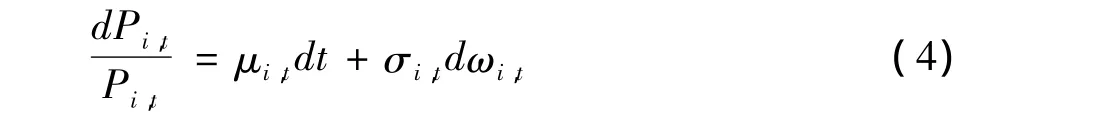
其中,两个参数分别表示价格的均值和方差,而ωi,t则代表股价服从维纳过程。因此效用最大化问题可化为如下问题:
由于动物的年龄、免疫状态、环境因素以及病原的感染数量的差异,临诊上发病猪的病程可分为最急性型、急性型、亚急性型和慢性型。
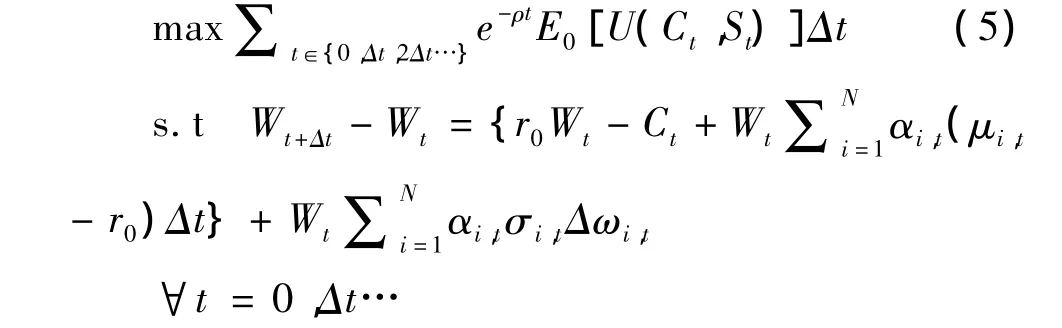
求解该问题可得如下欧拉方程:
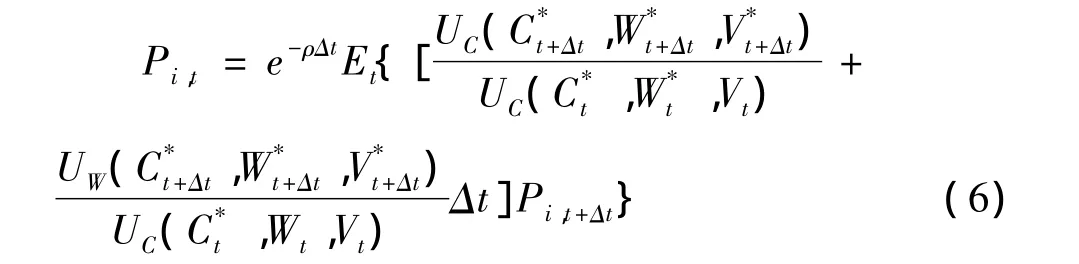
依照(3)式所定义的效用函数,我们可经过一系列代换,并引入消费,财富和资产的收益率,分别用RC,RW,Ri表示,可以得到我们的核心方程:
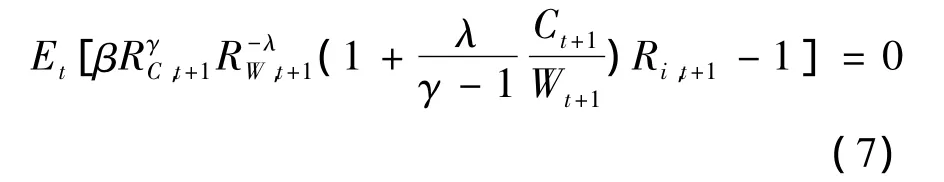
其中β=e-ρ。依据该方程,我们可以进行参数估计并进行“资本偏好”的假设检验。
三、模型估计
(一)计量模型
由于(7)式是一个条件期望的方程,给定t期的信息我们可以构造若干个矩条件,参照以往文献的方法,我们使用GMM的方法来估计这个结构模型的参数 γ 和 λ[8-11]。
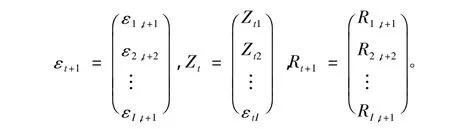
令:

其中ΩT为加权矩阵,(9)式即为GMM估计的目标函数,则最小化(9)式得到一阶条件:
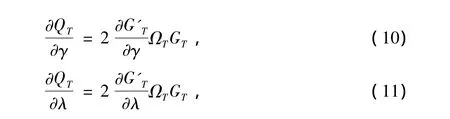
其中,
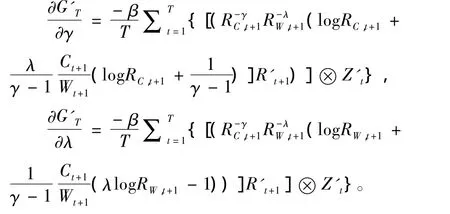
由于(10)、(11)式高度非线性,我们可以使用Newton-Raphson的方法进行迭代估计,直至收敛。
(二)数据描述
在进行缩减式方程的非线性GMM估计之前,首先要进行数据的统计描述。我们选取的时间区间是2000年1月至2010年12月,理由是这段时间中国的资本市场处于稳步前进的阶段,过早的不稳定的数据会带来模型估计的不稳定性,因此我们在此仅从2000年1月的数据开始。下表给出了估计数据的常用统计量。
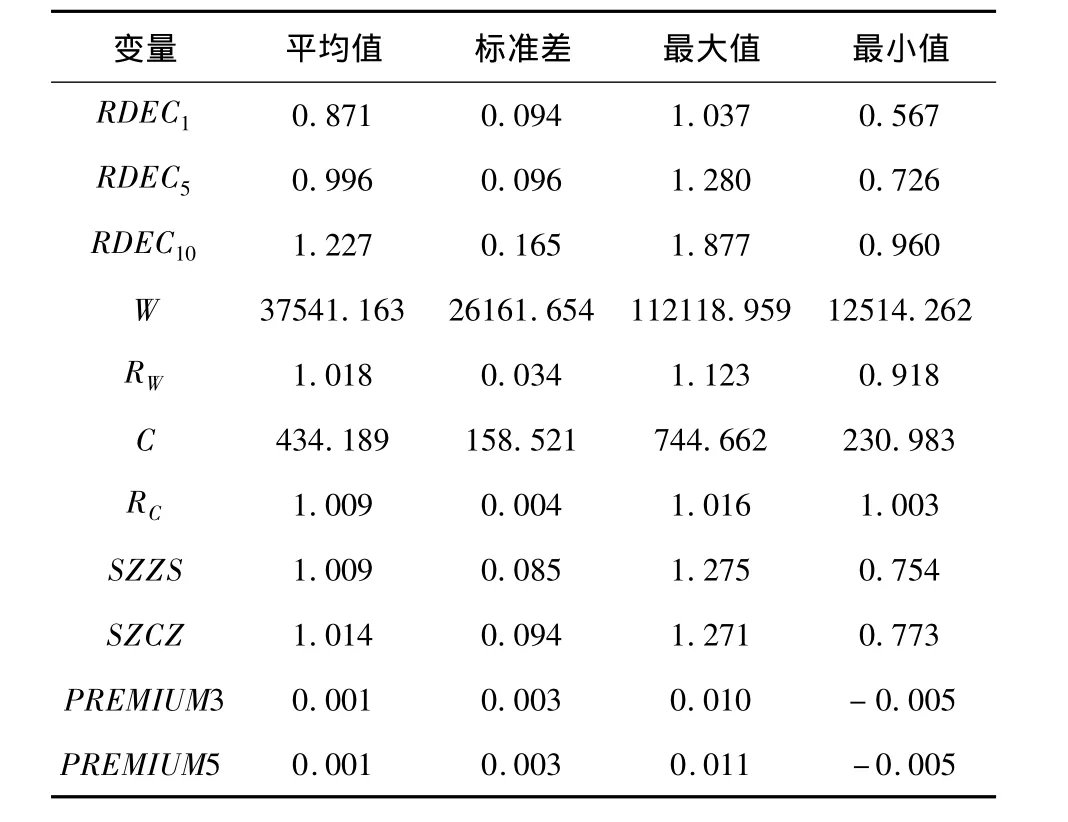
表1 描述性统计
表1中RDECi代表风险资产月收益率,数据来自于RESSET金融数据库。其处理方法是将每个月的所有流通股票的月收益率进行排序,根据其收益率大小均分为10组,每组资产成为一个大的资产组合,如i=1代表收益率最小的资产组合。假设该组资产的组合形式为等权重,因此收益率即为简单的代数平均。这种资产引入的原因是需要考察在不同收益率的资产下是否存在由财富和地位追逐所导致的资产价格的波动性。我们在此仅引入三组资产组合,即收益率处于最小、中等和最大的资产组合。从数据描述中可以看出,随着收益率组合的增大,波动率也在上升,这表明股票的收益率越高,波动性越剧烈。
W和RW代表中国人均财富以及财富的月增长率,数据来自于中国人民银行网站及RESSET数据库。研究美国的资本主义精神时,财富的代理变量是NYSE市值[6]。但在本文中,我们基于中国的实际情况有不同的考虑。美国是一个完全私有化经济,国民大部分财富确实投入于资本市场,用NYSE市值是财富的一个很好近似。而中国的资本市场的不完善导致其价值积累效应的薄弱。因此我们不能单纯考虑资本市场市值。考虑到中国居民的财富大部分以货币的形式持有,并不进入资本市场,我们这里定义的国家总财富 =M2+沪市市值+深市市值。我们认为这是中国国民财富的一个较好体现。将其除以总人口便得到人均财富。人均财富的增长率也可由此得到。由表1可以看出,国民财富的波动率非常剧烈,达到了均值的2/3。这也暗含了资本市场的不稳定。
C和RC代表中国人均消费和消费的增长率,数据来自于《中国统计年鉴》(2000-2009)。其中为了克服月度数据的缺陷,对数据进行了平滑处理,假设年内的消费增长率一致,但跨年不一致,采用插值方法进行估计,并对2010年的人均消费进行了固定增长率的推演预测。数据描述可以看出近10年来中国的消费水平大幅提高,前后翻了三番。
SZZS和SZCZ代表上证指数和深圳成分指数的月收益率,数据来自RESSET金融数据库。这是模型的两个工具变量,均已进行滞后两期处理。
PREMIUM3和PREMIUM5代表3年期国债和5年期国债与同期定期存款利率的利率差,数据来自于财政局网站及中国人民银行网站。这两个变量同样作为模型的工具变量出现,代表的是一种风险溢价的信息。数据中有一个较为惊人的发现,即溢价在某段区间内出现负值,即同期存款利率比国债利率高,我们认为这种现在来自于利息税的作用,但作为一种市场信息的反映,仅需要反映其相关关系,我们认为并不需要加以调整。
(三)估计结果
由于我们使用的是Newton-Raphson的方法进行迭代估计①若需要具体估计的代码,请向作者索取。,而(9)式的凸凹性比较复杂,一般迭代只能得到满足(10)、(11)式的局部稳定点。为得到(9)式的(伪)全局最小值点,我们选取了[-10,10]×[-10,10]内均匀分布的41×41组初值进行了迭代,首先使用单位矩阵进行加权,在局部稳定点中选取其中的最小值点作为参数的初步估计值和。其次再以此初步估计值构造最优加权矩阵=,其中为εt+1在^γ和上的取值。最后继续以上述41×41组初值进行迭代,在此次迭代中选取(伪)全局最小值点作为最优 GMM 估计值。我们分别对 RDEC1、RDEC5、RDEC10三组资产以及联合这三组资产的资产组合进行了上述估计,每组估计也分别进行了无限制估计以及限制估计,结果如表2所示。

表2 欧拉方程的GMM检验
从表2中可见,非限制条件下,γ的估值范围在-21.55 ~15.61,各种情况下都显著不为零,并且随着收益率的递增,γ值逐渐增加,这与收益和风险成正比的关系相一致。λ的估值范围在1.47~8.76,也都显著不为零 。对于RDEC5和RDEC10,γ≥1且λ>0的条件满足,但是对于收益率最低的那组资产组合,值为-21.55,与另外两组的值差别很大,出现这个异常值,我们猜测与交易收益率最低资产组合的投资人行为有关。因为投资这组资产组合的行为人可能有很强的风险偏好,属于偏好投机的类型,所以才会出现很低的值。
在3组资产组合的估计中,JT,U值都超过χ2临界值,过度识别假设都被拒绝。在限制条件下,~JT值相比较JT,U有较大变化,说明限制条件被拒绝,非限制条件下股价波动能被更好解释。综合来看,单个资产组合的估计结果支持“资本偏好”存在的假说。
由于对这3组资产的资产组合的过度识别限制Sargan检验没有通过,显示我们对包含整个资产组合的欧拉方程所构建的结构模型设置错误。同时我们尝试去掉 2个信息工具变量 (PREMIUM3,PREMIUM5)后再次进行估计,但仍通不过Sargan检验。我们猜测,并非是我们选取的信息工具变量的问题,而是个人持有整个资本市场的所有资产作为投资的资产组合的理论假设在中国是不成立的。可能的解释是,不同中国投资者的风险偏好具有异质性,投资者不愿意投资一篮子资产组合,而更倾向于某类收益——风险组合的资产。如此,分别以各类资产(即 RDEC1、RDEC5、RDEC10这三类资产)为基础的Sargan检验可以通过,而以所有资产作为资产组合的Sargan检验无法通过。
四、结 论
本文通过在标准的新古典模型效用函数中加入行为人对财富的追逐效应,考察了“资本偏好”的存在对股票价格波动的影响,进而印证了经济行为人有“资本偏好”的假说。而该结果为理解当下中国高投资低消费的经济格局提供一种新的视角,如果高投资是由存有“资本偏好”的投资者对财富的追逐造成的,那对于中国经济结构的悲观预测或许应该再谨慎一些。
同时,我们上述提出的关于中国投资者风险偏好异质性的猜测也是我们下一步的研究方向之一。风险偏好由γ表示,我们可以使用随机效用模型来表示个人风险偏好的异质性,在获取适当的面板数据后,我们就可以估计参数的方差并检验我们的这个猜测。
[1] Kurz M.Optimal economic growth and wealth effects[J].International Economic Review,1968,9:348-357.
[2] Robson A J.Status,the distribution of wealth,private and social attitudes to risk[J].Econometrica,1992,60:837-857.
[3] Fershtman C,Weiss Y.Social status,culture and economic performance[J].The Economic Journal,1993,103:946-959.
[4] Zou Hengfu.The spirit of capitalism and long-run growth[J].European Journal of Political Economy,1994,10:279-293.
[5] Zou Hengfu.The spirit of capitalism and savings behavior[J].Journal of Economic Behavior and Organization,1995,28:131-143.
[6] Bakshi G S,Chen Zhiwu.The spirit of capitalism and stock-market prices[J].American Economic Review,1996,86:133-157.
[7] Smith W T.How does the spirit of capitalism affect stock market prices?[J],Review of Financial Studies,2001,14:1215-1232.
[8] Hansen L P.Large sample properties of generalized method of moments estimators[J].Econometrica,1982,50(6):1029-1054.
[9] Hansen L P,Heaton J and Luttmer E G.Econometric evaluation of asset pricing models[J].Review of Financial Studies,1995,8(2):237-74.
[10] Hansen L P,Jagamathan R.Implications of security market data for models of dynamic economies[J].Journal of Political Economy,1991,99(2):225-62.
[11] Hansen L P,Singleton K J.Generalized instrumental variable estimation of nonlinear rational expectations models[J].Econometrica,1982,50(6):1269-1286.

