信用突变下商业银行信用风险测度模型研究——基于熵权物元可拓的分析

顾海峰

(东华大学旭日工商管理学院，上海200051)

一、问题的提出及研究述评

金融市场信息不对称的存在，将诱发借款企业的高风险博弈行为，从而引发逆向选择与道德风险问题，成为商业银行信用风险生成的潜在“隐患”。出于信用风险控制需要，商业银行实施“信贷配给”机制将成为信贷市场的“常态”，促使中小企业陷入融资困境［1］。对此，Stiglitz、Banerjee、Berger、Alian等学者试图通过引入中小银行方式来解决中小企业融资难题［2-6］。然而，Baltensperger认为，引入中小银行仅仅是银行内部分工，无法缓解中小企业融资困境［7］。事实上，信贷配给现象在农村金融市场同样存在，已严重制约了中小企业群体的快速发展［8］。对此，顾海峰研究发现，引入担保机制可以提升中小企业的平均信用等级，从而加大商业银行的放款意愿，以此来缓解中小企业融资困境［9］。但是，现行信贷模式所呈现的银保之间孤立式运作、缺乏协作性的特征，使得商业银行无法通过担保机制来有效转移信用风险，因为一旦担保机构债务代偿能力不足，可能成为商业银行信用风险的另一来源。对此，顾海峰认为，贷款企业是商业银行与担保机构信用风险的共同来源体，通过建立银保协作机制，可以构筑应对贷款企业信用风险的“双重防火墙”，以此来降低信贷配给幅度，提升金融市场信贷配置效率［10］。因此，推行银保协作型信贷模式是完全可行的。

在银保协作型信贷模式下，强化对来自于贷款企业层面的信用风险测度，已成为商业银行信用风险管控的重要内容。所谓信用风险测度，就是信用风险度量，属于信用风险识别范畴。商业银行实施信用风险测度机制主要存在于贷款的事前审核环节，商业银行通过对贷款企业实施信用评估，将信用等级不足的高风险贷款企业排除在放款群体之外，有效抑制了来自于贷款企业层面的信用风险，为商业银行实现信用风险管控目标提供了重要保障。

然而，全球金融危机、欧债危机等引发了国际经济运行的较大波动，对我国宏观经济运行将会产生一定的影响，并可能加剧我国宏观经济运行的波动性，这种波动性将传导到实体经济，从而促使企业经营状况发生波动，此外，国内货币政策、财政政策、产业政策的转变可能也会导致企业经营状况的变化。可见，国内外经济运行的波动性将使得信用突变可能成为一种“常态”。在这样的背景下，基于模糊评估方法的信用风险测度模型仅适用于信用平稳状态下的信用风险测度，而对于信用突变情形则存在较大的功能局限，因为模糊评估方法中依赖于专家打分方式来界定权重显得过于主观与粗糙，对于测定结果缺乏一定的平滑性与客观性，一旦发生较小的信用突变，则会导致信用风险等级的“过度跳跃”，影响到信用风险评估结果的准确度，难以为商业银行信贷决策提供科学依据。对此，本研究认为，采用熵权物元可拓方法可以很好的解决信用突变状态下商业银行信用风险的测度难题。原因在于:一方面，物元可拓方法中引入“距函数”来定义“关联度”，使得物元可拓方法对于商业银行信用风险的测度结果具有较好的平滑性;另一方面，引入信息熵方法来设定商业银行信用风险测度模型的权重，可以使得商业银行信用风险的测度结果更具客观性。正是在这样的背景下，本研究针对“信用突变下商业银行信用风险测度模型研究——基于熵权物元可拓的分析”问题展开深入探讨。

对于商业银行信用风险测度方面的研究成果，主要集中于两个层面。其中:在商业银行信用风险测度的研究视角层面，梁凌、杨继光等从经济资本视角来探讨商业银行信用风险的测度问题，依据新巴塞尔资本协议对于经济资本的界定，基于经济资本充足率管理路径提出了商业银行信用风险的测度方法［11-12］;谭燕芝、汤婷婷、华晓龙等从宏观经济视角来测度商业银行信用风险水平，通过分析宏观经济变量与商业银行信用风险之间的关联性，并基于宏观经济运行状态来测度及评价商业银行信用风险水平［13-15］。在商业银行信用风险测度的研究方法层面，柳玉鹏等运用组合评价方法对商业银行信用风险实施评价［16］;郭英见等采用信息融合技术构建了商业银行信用风险测度模型［17］;吴冲等基于模糊积分支持向量机集成技术建立了商业银行信用风险评估模型［18］;白保中等运用Copula函数法测度了我国商业银行资产组合中的信用风险水平［19］。

综上所述，现有文献主要集中于信用平稳状态下的商业银行信用风险测度模型及方法，而对于信用突变状态下的信用风险测度问题很少涉及，对此，本研究的贡献在于:基于信用突变思路，运用物元可拓理论与信息熵理论相融合的熵权物元可拓方法，构建了信用突变下商业银行信用风险测度模型，解决了信用突变下商业银行信用风险测度问题。本研究成果将为商业银行构建科学高效的信用风险管控机制提供重要的理论指导与决策参考。

二、基于物元可拓与信息熵的熵权物元可拓方法

熵权物元可拓方法是物元可拓理论与信息熵理论相融合的结果。其中:物元可拓理论的主要功能是建立测度对象的物元矩阵;并依据测度对象的等级分布状况，确定测度对象各等级所对应的经典域物元矩阵及测度对象的节域物元矩阵;在此基础上，通过“距函数”来计算关联度。而信息熵理论的主要功能在于解决权重的设定问题，使得权重设定更具客观性。

下面，本研究将以信用风险为测度对象，通过对传统物元可拓理论与信息熵理论的改进与拓展，给出适用于信用突变状态下商业银行信用风险测度的熵权物元可拓方法。

(一)建立测度对象的物元矩阵

我们将信用风险作为测度对象，以M表示，C为测度对象的特征指标集合，x为特征指标的相应取值。其中:测度对象M具有n个特征指标，则C={C1，C2，……，Cn};设第 k个特征指标 Ck的取值为xk，则 x={x1，x2，……，xn}。于是，测度对象 M、测度对象的特征指标C、特征指标的取值x组成了物元R的三要素，可表示为:物元R=(M，C，x)。

依据物元R的定义可知，物元R是融合了测度对象、测度对象的特征指标及特征指标取值三个要素的有序三元数组，通过将测度对象、特征指标及特征指标取值放在一个统一体中进行整体分析，可以准确揭示测度对象运行及分布的基本规律。鉴于物元R中测度对象M具有n个特征指标，我们将物元R称为n维物元，并给出如下形式的物元矩阵［20］:

(二)确定经典域与节域物元矩阵

我们将测度对象M划分为l个测度等级，即:M={M1，M2，……，Mt}，相应地，测度对象的各个特征指标Ck均具有l个测度等级，则特征指标Ck对应于各个测度等级的标准区间为{［ak1，bk1］，［ak2，bk2］，……［akl，bkl］}，且满足:(ak1，bk1)∩ (akj，bkj)=φ，(i≠j)，即任意两个开区间互不相交。于是，测度等级Mi的经典域物元矩阵为:

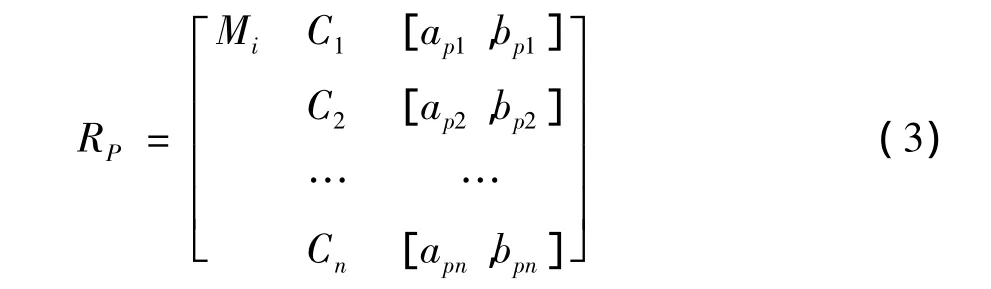
(三)基于距函数的关联度计算

为衡量点到区间的“距离”，我们引入泛函分析中的“距”，这里的“距”不同于欧氏几何空间中的“距离”，主要用以识别某个元素与给定元素集合之间关系的“疏密程度”。对此，我们对“距”进行量化，给出如下形式的距函数:若X以表示区间［a，b］，x为任意实数，则实数x到区间［a，b］的“距”可表示为 ρ(x，X)，则有:

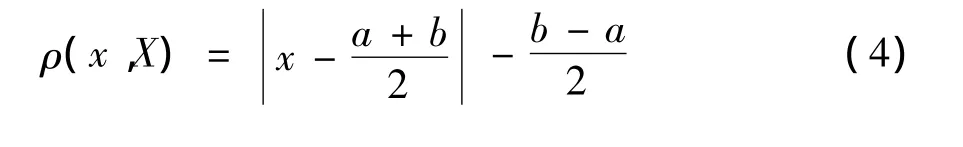
从距函数的表达式可知:若x∈X，则ρ(x，X)＜0;若 x ∉ X，则 ρ(x，X)＞ 0。

为了进一步刻画实数x与区间［a，b］之间的归属程度，我们将［a，b］拓展到［c，d］，使得满足:［a，b］⊂［c，d］，拓展后的区间［c，d］以 Y 表示，并结合距函数，可计算出实数x与区间［a，b］之间的关联度K(x)，即:

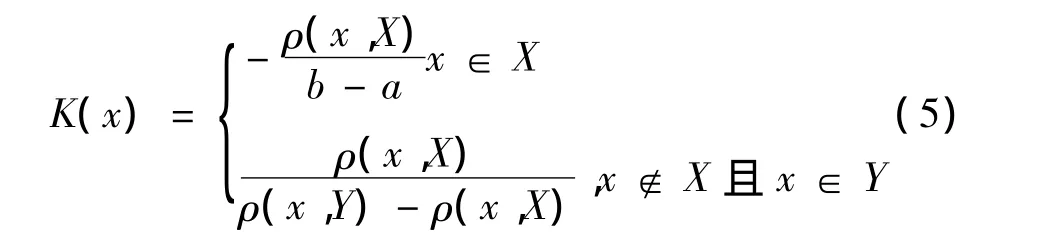
从关联度K(x)的表达式可以发现，关联度具有很好的平滑功能，其形式类似于“样条函数”。若以(x)表示待测样本第j个测度指标的实际取值与第i个测度等级(标准区间)之间的关联度，则待测样本对应于测度指标Cj的关联度集合为:

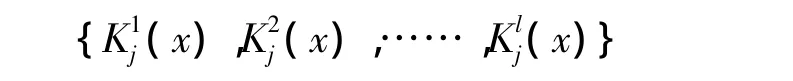
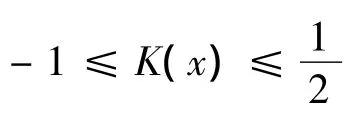
(四)基于信息熵的权重系数设定

信息熵方法来源于信息学科，等于不确定性信息量的概率预期，用以反映不确定性程度。即某测度指标的信息熵数值越大，则意味着该测度指标的不确定性程度越高，也就是说，该测度指标对测度对象的影响越小，而测度指标对测度对象的影响具有权重含义。为便于分析，我们选取m个待测样本，各个待测样本的测度指标取值以矩阵D表示:

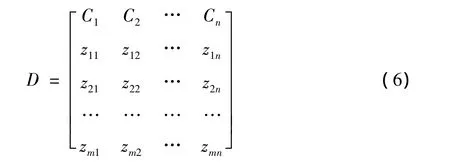
设Ej为测度指标Cj的信息熵。因信息熵是概率的连续函数，因此，对m个待测样本中测度指标Cj的实际取值(即:矩阵D的第j列元素)进行归一化处理，得到:

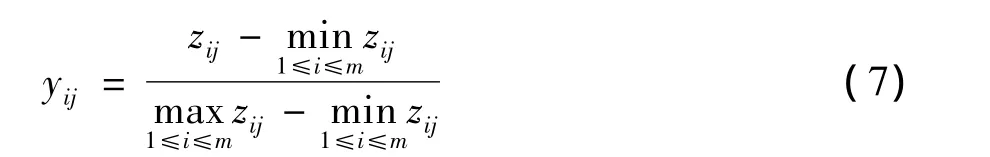
为保证对数运算有意义，且还要满足概率分布，对归一化后的矩阵列再进行如下运算:

显然，{H1j，H2j，……，Hmj}满足概率分布，且适用于对数运算。于是，依据信息论中对于信息熵的定义，即可得到测度指标Cj的信息熵为:

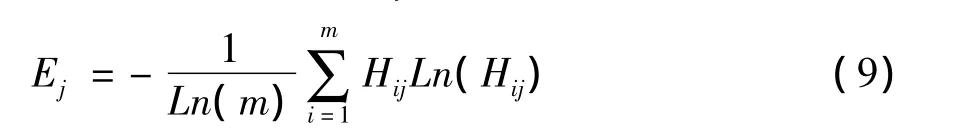
运用数学分析中的多元函数的拉格朗日极值定理，不难证明0≤Ej≤1，此外，信息熵Ej与测度指标Cj的影响度成负相关性，我们以偏离度1－Ej来衡量测度指标Cj的影响度，即可得到Cj对测度对象的相对影响程度，即Cj的权重系数，以wj表示:

(10)式即为无偏好情形下基于信息熵的权重设定法，对于存在偏好情形的权重设定，只需要添加偏好系数ηj，且进行如下修正:

三、基于熵权物元可拓的商业银行信用风险测度模型

下面，本研究将依据熵权物元可拓方法，以商业银行信用风险为测度对象，来构建商业银行信用风险测度模型。

(一)设定信用风险的测度指标及测度等级

商业银行信用风险的高低程度主要取决于贷款企业的信用状况，贷款企业信用等级越高，则商业银行所面临的信用风险程度就越低，因此，商业银行信用风险的测度指标设计应定位于对能够反映贷款企业信用状况的各个指标的选取。对此，本研究将从财务与非财务两个层面来设定衡量贷款企业信用状况的指标。其中:从财务层面来分析，应选择的指标主要包括经营水平指标、盈利水平、偿债水平等三个指标。从非财务层面来分析，应选择的指标主要包括管理水平、领导水平、履约水平、创新水平、发展潜力水平、生态环境水平等六个指标。上述九大指标已涉及对贷款企业的主观道德风险与客观偿债风险的双重反映，对于准确测度商业银行的信用风险等级提供重要基础。

由于商业银行面临来自于贷款企业的信用风险程度与贷款企业信用状况成负相关性，本研究将信用风险测度等级分为五级，分别为正常、轻度、中轻、中度、重度，分别对应于贷款企业的信用等级为优、良、中、一般、差。

(二)建立信用风险的经典域与节域物元矩阵

考虑到九大测度指标的实际取值范围是可控的，本研究对所设定的九大测度指标进行了无量纲处理，并进行归一化运算，使得信用风险的九大测度指标取值范围分布于［0，1］区间内，测度指标的取值越大，则表示待测样本在该项指标上表现越优。同时，为便于实际操作，本研究采用均匀分割法对［0，1］区间进行五等分割，可得到各个测度指标的标准区间，测度指标Cj(1≤j≤9)的标准区间集合为:{［0.8，1］，［0.6，0.8］，［0.4，0.6］，［0.2，0.4］，［0，0.2］}。此外，依据物元可拓的方法，本文的研究对九大测度指标进行可拓分析，分析后发现区间［0，1］符合拓展条件，可作为节域物元矩阵的拓展区间。于是，建立信用风险的经典域与节域物元矩阵如下:

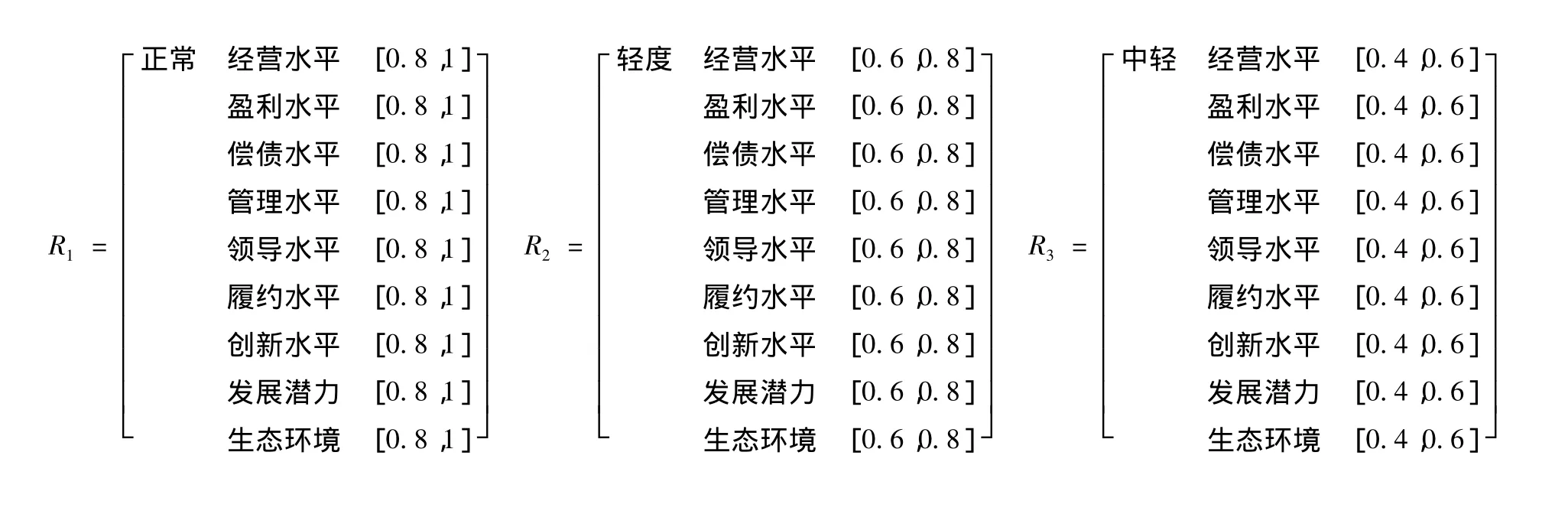
(三)设定权重及计算综合关联度

下面，本研究将依据信息熵方法，来设定信用风险测度指标的权重系数。对此，本研究选取m个待测样本(贷款企业)，提取m个待测样本的九大测度指标的实际取值，再结合信息熵方法，即可得到九大测度指标对信用风险的权重系数集合为:

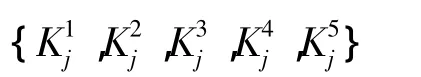
依据上述结果，本研究将计算出该待测样本与五大测度等级之间的综合关联度。我们以Ki表示该待测样本与第个等级之间的综合关联度，于是:

依据(12)式，即可得到该待测样本与五大测度等级之间的综合关联度集合为:{K1，K2，K3，K4，K5}

(四)判别信用风险的测度结果

依据该待测样本与五大测度等级之间的综合关联度，本研究将给出评信用风险测度结果的判别方法。综合关联度是对信用风险各个测度指标所属等级的加权平均，因此，综合关联度能够很好地反映待测样本对于各个测度等级的归属程度，若待测样本与某个测度等级之间的综合关联度越大，则该待测样本归属于该测度等级的可能性越大。依据上述判别思路，本研究对测度结果给出如下的判别方法:

更进一步地，若两个待测样本P、Q具有相同的风险等级，即:待测样本P、Q均被确定为Ki(1＜i＜5)等级，则判别待测样本P、Q优劣顺序的依据是:将待测样本的综合指标值与Ki等级的两相邻等级之间的综合关联度进行比较，若样本P满足关系式Ki－1＞Ki+1，且样本Q满足关系式Ki－1＞Ki+1，则可认为样本企业P的信用风险状况略优于样本企业Q。

四、商业银行信用风险测度模型的实证分析

下面，我们选取江苏苏州地区的3家普通贷款企业作为待测样本，其中:3家样本企业的财务数据来自于2012年6月30日3家样本企业的财务报表。通过对3家贷款企业财务数据的分析，并对3家贷款企业所处行业的平均增长水平及产业环境进行了综合分析与预测，得到3家贷款企业(待测样本)的实际数据，分别以如下的物元矩阵表示:

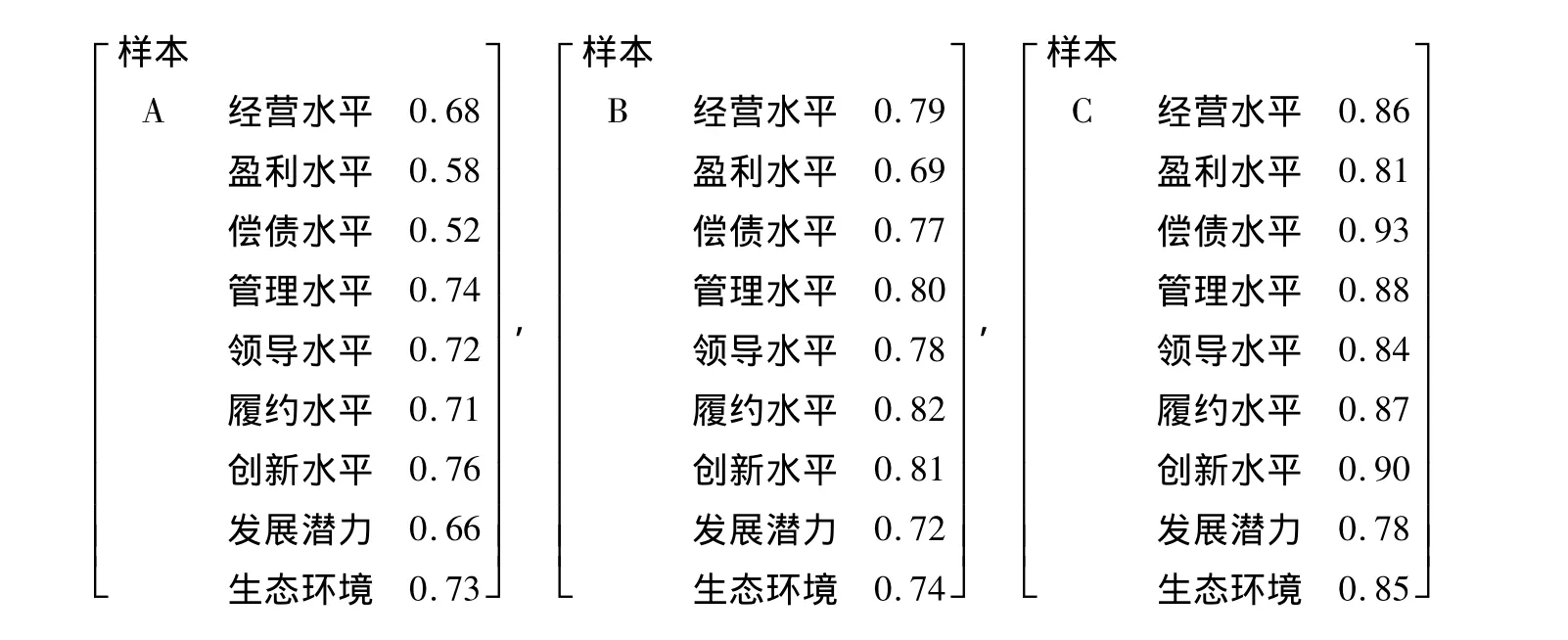
依据上述数据，结合本研究给出的信用风险测度的经典域与节域物元矩阵，并运用关联度计算方法，我们可得到3家样本企业指标与九大测度等级指标之间的关联度，见表1。

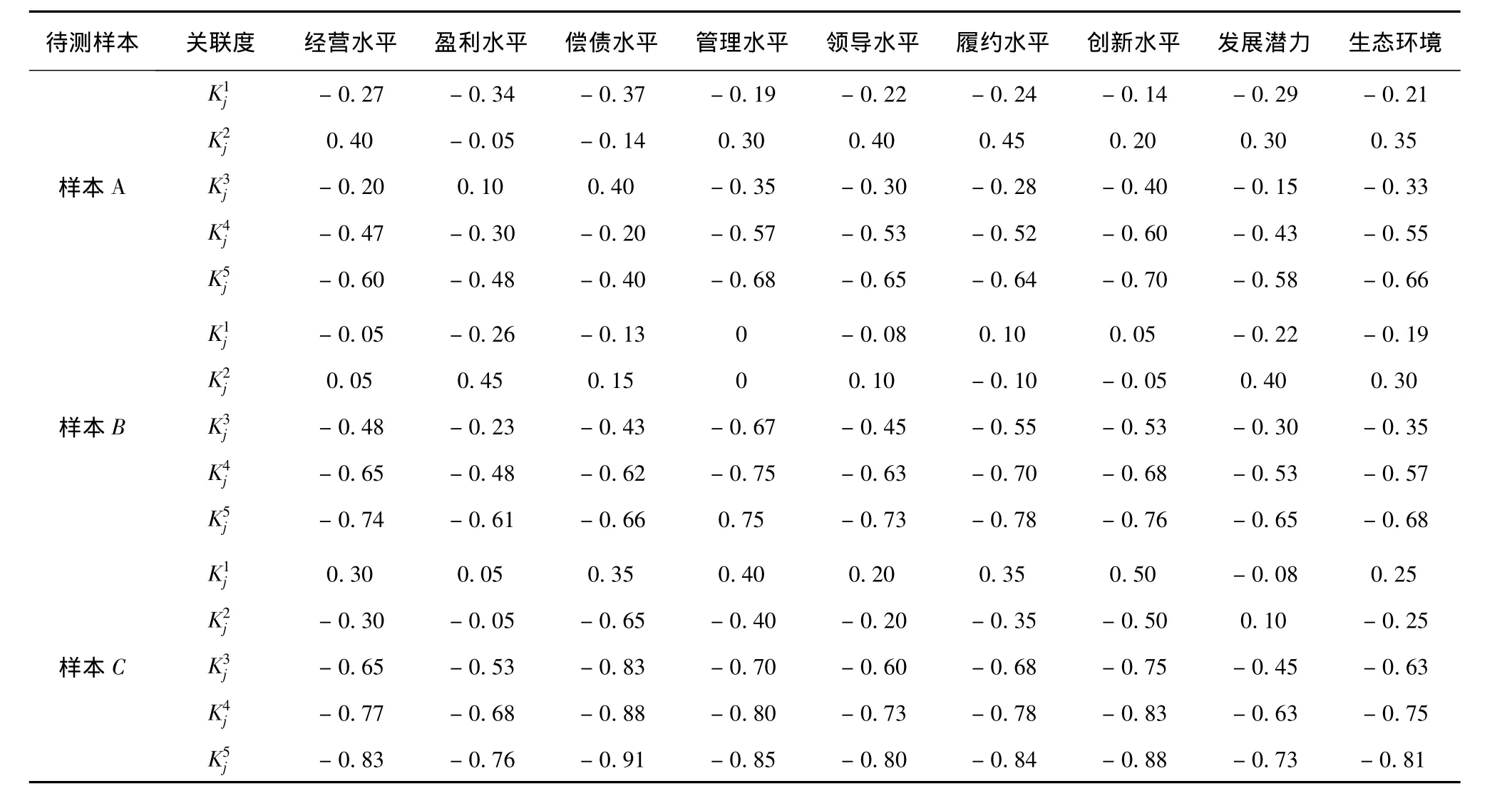
表1 样本企业指标与九大测度等级指标之间的关联度

依据上述表1中计算得到的3家样本企业指标与九大测度等级指标之间的关联度，本研究采用信息熵权重计算方法。此外，本研究在权重系数的计算过程中，对偿债能力等几个指标设置了一定的偏好系数，以强化商业银行对信用风险的控制目标。于是，依据公式(11)给出的基于偏好信息熵的权重计算方法，我们得到九大测度等级指标对商业银行信用风险影响的权重系数，具体结果见表2。

表2 基于有偏好信息熵的测度指标权重系数

通过表1提供的关联度数据，结合表2中各个测度指标的权重系数，本研究运用公式(12)给出的综合关联度计算方法，即可得到3家样本企业的综合关联度，并依据本研究给出的测度结果判别方法，对3家样本企业进行了信用风险等级的确定，具体结果见表3。

表3 样本企业综合关联度及信用风险等级

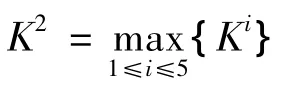
此外，本研究通过对样本企业A与B的结果进行比较发现，尽管样本企业A与B的信用风险等级均为轻度，但是，通过对样本企业A与B的综合关联度分析，发现两者在信用风险等级方面还是存在一定的优劣顺序。原因在于:样本企业A的综合指标值与经度等级的两相邻等级之间的综合关联度存在关系式K1＜K3，显然，样本企业A的综合指标值明显趋近于中轻等级;而样本企业B的综合指标值与经度等级的两相邻等级之间的综合关联度存在关系式K1＞K3，显然，样本企业B的综合指标值明显趋近于正常等级。依据判别方法，即可得到如下结论:尽管样本企业A与B的信用风险等级均为轻度，但是，样本企业B的信用风险状况整体上略优于样本企业A。

五.结论与展望

在信用突变状态下，传统的模糊评估方法已表现出较大的功能局限性，难以实现信用风险测度结果的准确性，对此，本研究通过将物元可拓理论与信息熵理论的相互融合，提出了熵权物元可拓方法，在此基础上，构建了基于熵权物元可拓方法的商业银行信用风险测度模型，并对测度模型进行了实证分析，研究表明，通过引入熵权物元可拓方法，信用突变引发贷款企业各个信用指标取值的变化，并没有导致来自于贷款企业的信用风险测度等级的“跳跃”，足以说明熵权物元可拓方法具有较好的平滑性与客观性功能，因此，基于熵权物元可拓的商业银行信用风险测度模型科学地解决了信用突变状态下的信用风险测度难题。

此外，构建科学高效的商业银行信用风险测度模型，是实现商业银行信用风险管控目标的重要路径，特别是在全球经济环境与经济运行态势存在较大不确定性与突变性的现实背景下，强化对信用突变状态下商业银行信用风险测度模型的研究，对于我国银行业防范与控制信贷风险具有非常重要的理论与现实意义，对此，这方面研究还有待于进一步深化，本研究成果将为这方面研究提供基础性铺垫。

［1］ Arrow J.The economics of information［M］.Basil Blackwell Limited，1994.

［2］ Stiglitz J E，Weiss A.Credit rationing in markets with imperfection information［J］.American Economics Review，1991，71(3):393-410.

［3］ Banerjee A V，Besley T G.The Neighbour′s keeper:The design of a credit cooperative with theory and a test［J］.Quarterly of Economics，1994，3:107-110.

［4］ Berger A N，Udell G F.Relationship lending and lines of credit in small firm finance［J］.Journal of Business，1995，18:230-242.

［5］ Berger A N ，Udell G F.Small Business credit availalibity and relationship lending:The importance of bank organizational structure［J］.Journal of Economic Forthcoming，2002，15:613-617.

［6］ Riding A L，HainesJR G.Loan guarantees:Costs of default and benefits to small firms［J］.Journal of Business Venturing，2001，16:595-612.

［7］ Baltensperger E.Credit rationing:Issues and questions［J］.Journal of Money，credit，and Banking，1998，10(2):170-183.

［8］ 蔡四平，顾海峰.农村中小企业金融市场的信贷配给问题及治理研究［J］.财贸经济，2011(4):19-24.

［9］ 顾海峰.信用担保机制下金融信贷配给的均衡演变研究［J］.求索，2008，1:10-12.

［10］ 顾海峰.中小企业金融发展的创新路径研究——信贷配给视角下银保风险协作机制的建构［J］.山西财经大学学报，2010(1):15-19.

［11］ 梁凌，彭建刚，王修华.内部评级法框架下商业银行信用风险的资本测算［J］.财经理论与实践，2008(1):13-18.

［12］ 杨继光，刘海龙.商业银行组合信用风险经济资本测度方法研究［J］.金融研究，2009(4):25-29.

［13］ 谭燕芝，张运东.信用风险水平与宏观经济变量的实证研究——基于中国、美国、日本部分银行的比较分析［J］.国际金融研究，2009(4):16-22.

［14］ 汤婷婷，方兆本.商业银行信用风险与宏观经济——基于压力测试的研究［J］.当代经济科学，2011(7):22-27.

［15］ 华晓龙.基于宏观压力测试方法的商业银行体系信用风险评估［J］.数量经济技术经济研究，2009(4):21-26.

［16］ 柳玉鹏，李一军.组合评价方法在银行信用风险评价中的应用［J］.中国管理科学，2008(10):23-27.

［17］ 郭英见，吴冲.基于信息融合的商业银行信用风险评估模型研究［J］.金融研究，2009(1):23-28.

［18］ 吴冲，郭英见，夏晗.基于模糊积分支持向量机集成的商业银行信用风险评估模型研究［J］.运筹与管理，2009(4):19-23.

［19］ 白保中，宋逢明，朱世武.Copula函数度量我国商业银行资产组合信用风险的实证研究［J］.金融研究，2009(4):21-25.

［20］ 蔡文.物元模型及其运用［M］.北京:科学技术出版社，1994.58-63.