STL模型的分区域面片删除简化方法

李日华,周惠群,刘 欢

(西北工业大学现代设计与集成制造技术教育部重点实验室,陕西西安710072)

快速成形(rapid prototyping,RP)技术是20世纪80年代末期发展起来的一项采用材料精确离散/堆积成形原理的新型制造方法,它需要由三维CAD模型切片求出每层的截面轮廓。

由于不同的CAD制造系统对实体的内部表达方式各不相同,直接对原CAD实体模型进行切片的方法在通用性上存在着很大缺陷,因此,目前广泛采用ST L文件在CAD和RP系统间进行数据交换[1]。

STL格式用于将三维模型近似成小三角形平面的组合,是后续数据处理的依据。如何减少数据运算量和存储量也是RP领域的研究热点之一。目前,最普遍采用的简化策略为几何元素删除法,其他还包括顶点删除法、三角形折叠法、迭代收缩法[2-3]等。Schroeder[4]提出的顶点删除法思想是判断每个顶点类型,根据不同类型选择不同判断依据;若满足设定的条件则将顶点删除,再对形成的空洞三角化。本文先将模型划分为一个个子区域,若某个子区域较平坦,则将其用更少的三角形面片进行重新划分,以减少模型中面片的数量,通过多轮简化以达到要求。

1 STL文件的子区域划分

1.1 STL文件间拓扑关系和毗邻表的建立

STL的每个三角形网格由它的3个顶点及单位法矢构成[5]。为了在整体STL文件中划分出一个较小的子区域,需知道每个面片与哪几个面片相邻,即建立面片之间的毗邻信息。

在一个没有错误的ST L文件中,每个面片应有3条边及3个相邻面片,两个共享一条边的面片可称为一对毗邻面片;不会有超过两个面片共享一边。

记某个面片的 3个顶点为 v1、v2、v3;用 Eij表示连接顶点vi和vj的边,其毗邻资料由一对数字(m,n)表示,m为毗邻面片的号码,n为毗邻面片中边的号码。n=0表示毗邻面片的边 E23,n=1表示毗邻面片的边 E13,n=2表示毗邻面片的边E12(图1)。

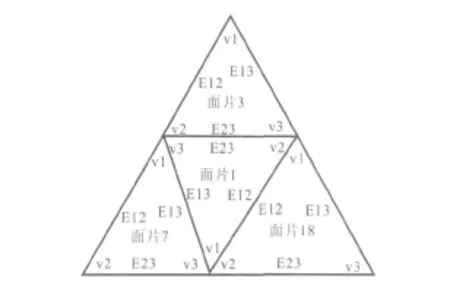
图1 面片1的毗邻面片

面片1中,E12与面片18的E12重合;E23与面片3的E23重合;E13与面片7的 E13重合。面片1的毗邻信息见表1。

表1 面片1的毗邻表

在对整个STL文件的遍历过后,就可建立起全部面片的毗邻信息表,即可精确查找到任意一个面片的毗邻面片,并知道二者之间的共用边及共用顶点。

1.2 子区域划分方法

本文将子区域定义为:由某个面片及所有与这个面片有公共顶点的面片所组成的集合(图2)。

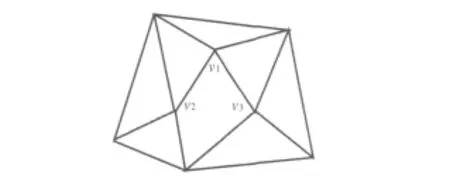
图2 采样面片及其确定的子区域

子区域是本文对STL文件进行简化的基本单位,基于毗邻信息表可得出某个面片所确定的子区域的查找方法。

由采样三角形(记为面片 i)的 E12边开始,找到其毗邻面片 j并对其进行标记。由STL文件的共顶点原则(一个小三角形平面的顶点不能落在相邻的任何一个三角形的边上)可知,在j的3个毗邻面片中必有另一个面片包含了顶点v2,找出这个面片并对其标记后,查找该面片的3个毗邻面片,其中一个就是面片 j,另外的两个中必有一个(记为 k)包含了顶点 v2。这又分为两种情况:一种是仅包含v2;另一种是包含了 v2及 v3(图3)。若是前者,可继续在k的3个毗邻面片中查找包含v2的面片并标记;若是后者,则说明k就是i中E23的毗邻三角形,接下来在k的毗邻面中查找包含v3的面片。

图3 新查找到的面片 k

这样,在绕着采样面片查找完毕后即可标记出所有与其共顶点的面片,即确定了一个子区域。

1.3 平坦子区域的判断

某个子区域中,所有相邻面片法向量夹角的方差可反映出这个区域里STL模型表面曲率变化的大小。可给定一个参数ε,当方差小于ε时,即认为该子区域平坦,可简化;当方差大于ε时,则保留此区域。

网格的单位法矢可由三角形的v1、v2、v3的连接顺序按右手规则确定。若顶点的坐标值为 xi、yi、zi(i=1,2,3),则该网格的单位法矢可由下式计算[5]:

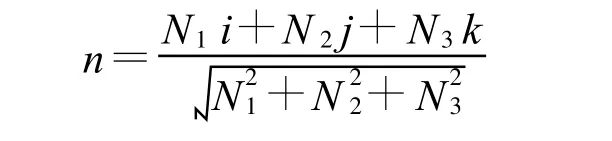
式中:i、j、k分别为沿 x、y、z 轴的单位矢量;N1=y1(z2-z3)+y2(z3-z1)+y3(z1-z2);N2=z1(x2-x3)+z2(x3-x1)+z3(x1-x2);N3=z1(y2-y3)+x2(y3-y1)+x3(y1-y2)。

由两个相邻面片的法矢即可算出它们的法向量夹角:

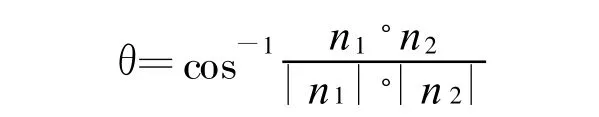
法向量夹角的方差为:

式中:E为期望,即平均值的符号;Eθ为子区域中相邻面片法向量夹角的平均值。该方差可反映出这个区域是否平坦。如果Dθ≤ε,即对这个区域标记为平坦[3]。

2 基于面片删除的子区域简化方法

2.1 面片删除及重新三角化

删除平坦区域内部所有的面片,并对其重新进行三角化。新生成的面片的边必须至少有一条为区域的轮廓边,这样重新进行三角化后,面片的数量会有所减少(图4)。

图4 子区域的简化方式

然而,在某个顶点周围连续出现多个狭长面片之后,区域轮廓可能变得非常复杂(图5)。

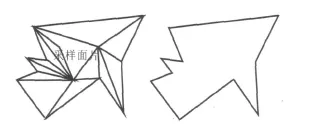
图5 复杂的轮廓

对复杂的轮廓进行三角化分为两个步骤:首先将其划分为 y-单调多边形,再对y-单调多边形进行三角化。需要指出的是区域轮廓严格上来说不是一个平面多边形,而是一组封闭的空间折线。但由于区域较平坦,本文的算法并不会受到影响。

2.1.1 子区域轮廓的y-单调块划分

如果对于任意一条垂直于直线 l的直线l′,多边形与 l′的交都是连通的,则该多边形为关于直线l单调的多边形(图6)。

图6 关于 l单调的多边形

设想,沿着一个普通区域轮廓p的左边界或右边界,从最高顶点走向最低顶点。在某些顶点处行进方向可能会从向下转为向上或从向上转为向下,这些顶点称为拐点。拐点可分为4类:起始顶点处的内角小于π,且其相邻两个顶点高度都比它低;分裂顶点处的内角大于 π,且其相邻两个顶点高度都比它低;汇合顶点处的内角大于π,且其相邻两个顶点高度都比它高;终止顶点处的内角小于π,且其相邻两个顶点高度都比它高。其余的顶点称为普通顶点(图7)。

图7 5种顶点

很明显,如果一个多边形里没有汇合顶点和分裂顶点,它就是y-单调的。为了消除这两类顶点,需在每个分裂顶点处向上连一条对角线,在每个汇合顶点处向下连一条对角线,且这些对角线两两不相交。

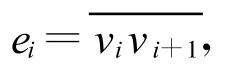
考虑ej与ek之间、位于 vi上方的那些顶点。若这些顶点中存在一个最低的,那就将它和vi连接起来组成一条对角线将vi消除,见图8a;如果不存在一个最低的,或 ej与ek间没有顶点,则将 vi与ej或ek的上端点连接,见图 8b和图 8c。这个与 vi连接的顶点叫做ej的助手——helper(ej),其定义是:helper(ej)是在当前扫描线上方、通过一条完全落在p内部的水平线段与ej相连的顶点中高度最低的那个顶点。至此可知,把分裂顶点与它左侧那条边的助手相连即可将其消除。

图8 分裂顶点的消除

如果将轮廓 p上下颠倒就会发现分裂顶点和汇合顶点发生了互换。因此,处理分裂顶点的思路也可用来处理汇合顶点。只需把某个汇合顶点vi与它左右两侧的边ej与ek之间、当前扫描线下方位置最高的那个顶点连接起来即可。虽然在扫描线刚触及vi时还不知道哪个是位于其下方位置最高的顶点,但至少已知vi是ej的新助手。图 9a中,扫描线向下进行到vm时发现它变成了ej的新助手,那么就在 vm和vi之间连一条对角线,消除了汇合顶点vi。因此,更换某条边的助手时,要检查被替换下的助手是否为一个汇合顶点。如果是,就在新、老助手之间连一条对角线。第二种可能见图9b,扫描线越过 vi后,ej的助手不再发生变化,就把vi和ej的下端点连接起来,也可将分裂顶点vi消除。

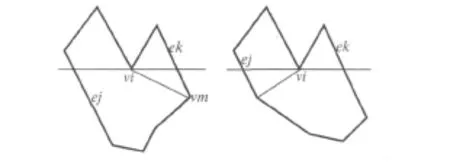
图9 汇合顶点的处理

2.1.2 y-单调块的三角划分

对某个y-单调块p而言,可从最高顶点开始同时沿着其左、右两条边界走向最低顶点,通过引入对角线完成三角剖分。

按照y-坐标递减的顺序依次处理各个顶点。当两个顶点y-坐标相等时,优先处理靠左的顶点。用一个栈s作为辅助数据结构。一开始栈s为空,在算法运行过程中,它存放 p中已被发现,却依然可生出更多对角线的顶点。在处理新顶点的时候,应尽可能在这个顶点与栈中的各顶点之间引入对角线,这些对角线会从p中分离出若干三角形。尚未从原多边形中分离出的顶点都散落在 p中尚未被三角剖分的部分与已处理过的部分之间的边界上。这些顶点中位置最低的那个就位于栈顶;高度次低的那个顶点位于次栈顶。在已被发现的那些顶点之上,p中还有一些尚未剖分的部分,这些部分的形状像一个金字塔。这个金字塔的一侧边界由 p的某条边独立界定,而另一侧边界上所有的顶点,除了最高处的那一个之外,其对应的内角都不小于180°(图10),这样的顶点称为凹顶点。

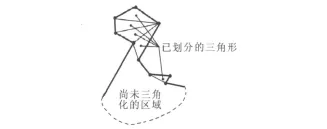
图10 已经三角剖分和未三角剖分的部分

在处理下一个顶点 vi时,分为两种情况:vj与栈中的凹顶点不在同侧(图11a),或位于同侧(图11b和图11c)。

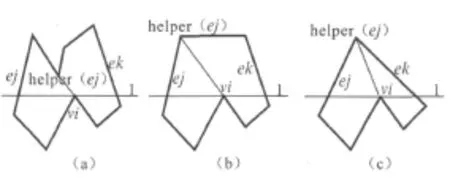
图11 接受处理的下一顶点的3种情况

可由 vj出发与当前栈中除了最后一个顶点之外的每个顶点连一条对角线。所有这些顶点连同栈中最后一个顶点一起从栈中弹出。此后在vj之上,原多边形中尚未三角剖分的部分将由刚刚生成的、连接 vj与栈顶顶点的那条对角线界定。该顶点及vj仍然属于多边形中尚待三角剖分的部分,要将它们重新压回栈中。

当vj与凹顶点同侧时,可按照如下方法处理:首先从栈中弹出一个通过 p的一条边与vj连接的顶点,然后依次从栈中弹出各顶点,并将其与 vj连接,不断重复这个过程。当遇到一个无法与vj相连的顶点后,就重新将被弹出的前一顶点压入。完成上述操作后将vj重新压入栈中。

对y-单调多边形完成三角化的算法如下:

算法:TriangulationP

输入:一个y-单调多边形p

输出:p的三角剖分

(1)将 p所有顶点按照y-坐标排成一个递减序列。若多个顶点 y-坐标相同,则 x-坐标较小的在前。令排序后的序列为 u1,u2,……un

(2)初始化一个空栈 s,压入 u1、u2

(3)for(j←3 to n-1)

(4)do if(uj处于与s栈顶定点对面一侧)

(5)then弹出s中所有顶点

(6)对弹出的(除最后一个之外的)每个顶点在uj与该顶点生成一条对角线

(7)将和uj压入s

(8)else弹出s的栈顶

(9)不断检查当前栈顶处的顶点:只要它与uj的连线完全落在p内部,就弹出该顶点。把这些连线作为对角线储存。将最后弹出的顶点压回s中

(10)将 uj压入s中

(11)将un与栈中除第一个和最后一个之外的每个顶点连成对角线。

2.2 子区域简化示例

以图5中的子区域轮廓为例,它含有一个分裂顶点和一个汇合顶点需要消除(图12a)。

图12 分裂顶点与汇合顶点的消除

按照本文的算法,分别对这两个顶点予以消除(图12b)。对划分出的y-单调块进行三角划分,通过对比可看出面片数量由14个减少为8个(图13)。

3 结语

本文采用将区域内的面片删除后进行重新三角划分的方法,分区域对STL模型进行简化。基于面片的毗邻表找到采样三角形确定的子区域后,以相邻面片之间法矢量夹角的方差为标准判断子区域是否平坦。保留了ST L模型表面较重要的、反映其细节或形状特征的区域,最大限度保留了模型视觉特征。通过控制简化循环次数、方差阈值来得到不同精度的简化模型。

图13 简化结果

[1]蔡小康.智能化的快速成形切片算法[J].中国机械工程,1997,8(5):49-51.

[2]余罗兼.反求工程中三角网格模型简化若干方法的研究[J].机电技术,2009(2):9-11.

[3]马淑梅,朱少斌,李爱平.采用顶点删除的STL模型分簇简化方法[J].现代制造工程,2012(1):79-83.

[4]Schroeder W J,Zarge J A,Lorensen W E.Decimation of triangle meshes[J].ACM Siggraph ComputerGraphics,1992,26(2):65-70.

[5]谢存禧,李仲阳,成晓阳.STL文件毗邻关系的建立与切片算法研究[J].华南理工大学学报(自然科学版),2000,28(3):33-38.