基于改进粗糙集和NSCT的红外遥感图像增强
王 琪,徐 川,路祥宇
(1.太原市基础地理数据中心,山西 太原 030009;2.武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079)
红外遥感图像增强是一种图像预处理手段,主要是对图像中的某些特征,如图像细节、边缘等进行增强,便于识别和后续分析处理。国内外对于红外遥感图像增强的研究大体可以分为2种:基于空间域的图像增强和基于变换域的图像增强。第一种方法大多是基于图像的灰度特征对图像进行增强,此类算法包括灰度拉伸、邻域滤波、直方图修正和形态学增强等[1-3],但大多忽略了图像的边缘信息与细节信息。第二种方法是将图像在变换域中进行去噪增强,此类算法包括基于傅里叶变换、基于小波分析和基于Contourlet变换等[4-8],但这些算法忽略了图像的空间位置关系。本文提出了一种基于改进粗糙集和NSCT的红外图像增强算法,有效地克服了传统算法的缺陷,使得增强后的图像更易于后续的图像处理工作。
1 NSCT和粗糙集理论
NSCT是由Contourlet变换发展而来的。由Contourlet变换的分解过程可知,在拉普拉斯金字塔(LP)分解阶段和方向滤波器(DFB)分解阶段,都采用了下采样,因此Contourlet变换不具有平移不变性。2005年,Cunha等人提出非下采样的Contourlet变换——NSCT(nonsubsampled contourlet transform)[9],利用非下采样的金字塔分解和非下采样的方向滤波器组分解构造NSCT,得到了灵活的多尺度、多方向、各向异性并且具有平移不变性的图像分解模式。
NSCT借鉴àtrous算法的思想[9],并不对LP分解后的分量和DFB分解后的分量进行下采样,以NSP分解代替,仅仅对滤波器进行上采样以获得平移不变性,分解过程通过非下采样金字塔滤波器组(NSPFB)进行。这样,下一级的滤波器系数可以通过对上一级的滤波器上采样得到,避免了额外设计滤波器,同时还获得多尺度特性。NSCT分为2个部分:非下采样LP分解和非下采样的DFB分解。和Contourlet类似,NSCT首先采用NSPFB对图像进行多尺度分解,然后再采用非采样方向滤波器组(NSDFB)对得到的各带通子图进行方向分解,从而得到不同尺度、方向的子带图像[9]。NSCT的重构过程与分解过程相反。
粗糙集理论通过不可分辨关系来建立各种关系,进行知识分类。在粗糙集理论中,事物或对象作为论域中的元素用其属性来描述,知识是人类对分辨事物建立起来的抽象和普遍性的概念,是一种根据对象属性来分类的能力。2个相差不大的物体在分类过程中归为同一类,它们之间的等价关系就是不可分辨关系[10]。
2 基于改进粗糙集和NSCT的图像增强算法
2.1 条件属性集和增强策略
我们定义一个条件属性集C∶C{c1,c2,c3},其属性定义如下:在图像空间域,定义c1为噪声属性,c1={0,1},1表示某处像素亮度与周围某一窗口内像素亮度梯度大于Q'(Q'为某一阈值),0表示其他。在NSCT系数域,可以定义为:c1是NSCT域噪声属性,c1={0,1},1表示在某一分解层高频子带中,此处系数在周围某一窗口内呈局部极大值且小于Q(Q为某一阈值),在其他层高频子带随层衰退;0表示其他。c2是NSCT域弱模属性,c2={0,1},通过分析子带中的系数模平均大小,在系数的某一范围,例如Max(Coeffs)/500以上,以I(x,y)表示该处系数模。1代表I(x,y)≤P, 0代表系数模I(x,y)>P(假设p为某一阈值)。c3是NSCT域方向模糊梯度属性,c3={0,1},在系数的某一平均范围以上,以Gf(x,y)表示该处系数方向模糊梯度相关值,0代表Gf(x,y)≤∆,1代表系数模糊梯度Gf(x,y)>∆(∆为某一阈值)。
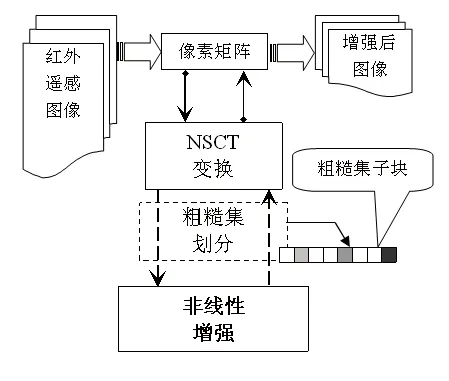
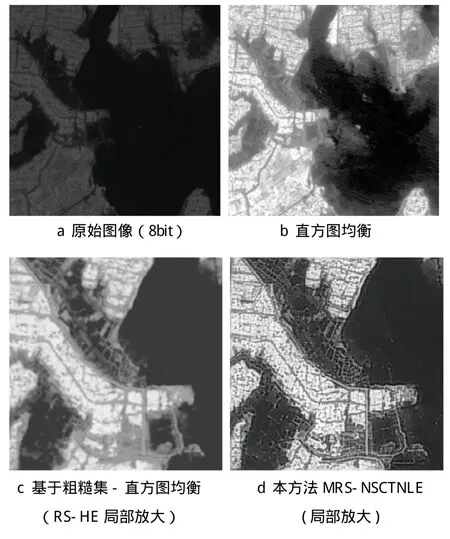
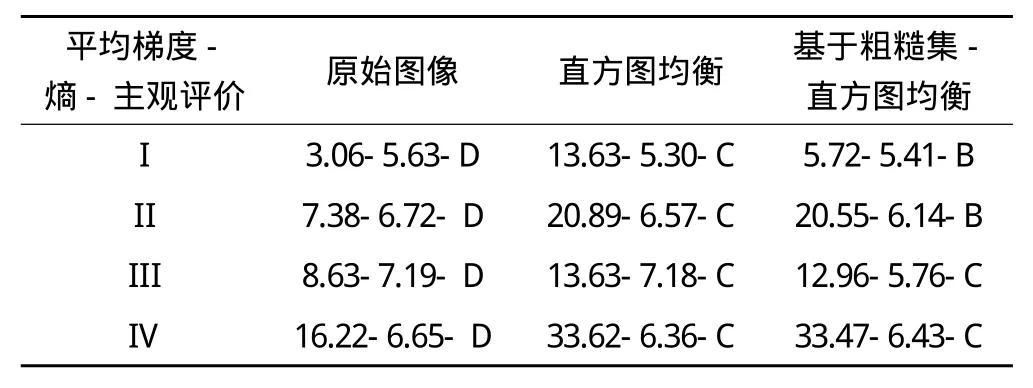
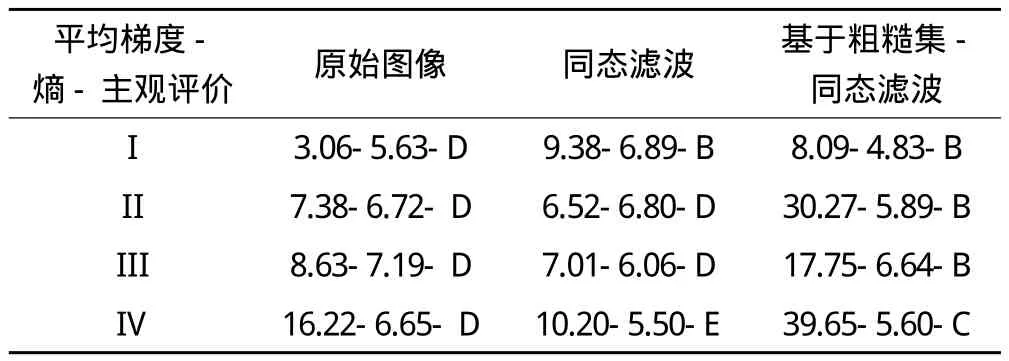
将系数按照c1的方式分解得到子图位平面RC1∶RC1(X)={x|:I(x,y)>Q且I(x,y)↓},RC1(X)代表噪声系数的粗糙集,代表非噪声系数粗糙集。将图像按照c2的方式分解得到子图位平面RC2∶RC2(X)={x|:Q 通过这个决策规则,我们将图像划分为噪声、弱边缘、强边缘3个子块。通过对3个子块采取不同的增强方法来达到对整幅图像进行增强的目的。不同子块增强策略如表1所示。 表1 不同子块的增强策略 1)将红外图像在空间域线性拉伸; 2)对拉伸后的红外图像进行NSCT 3层分解,比如2,4,8方向分解,获得各个尺度和各个方向的系数; 3)将每一层不同方向的高通子带进行粗糙集子图划分组成位平面,使用文献[11]中定义的模糊成员函数并加以不同的方向窗口约束; 4)通过模糊成员函数将系数方向梯度特征映射到相关的模糊平面,取值在[0,1]之间,在模糊域通过粗糙集划分和决策规则对每一个子图进行定义并进行不同程度的模糊梯度增强; 5)将增强后的系数转换到NSCT域,再进行图像重构获得增强后的图像,如图1所示。 图1 算法流程图 本实验主要就空间域和变换域2个方面进行,主要就直方图均衡、基于小波变换的非线性增强(WLTNLE)、基于NSCT的非线性增强(NSCTNLE)以及基于改进粗糙集的增强方法。加入了粗糙集规则(RS-)和改进粗糙集规则(MRS-)后,实验效果明显增强。 主观评价主要通过观察,判断图像增强后边缘是否清晰,噪声是否放大,是不是产生了虚假边缘信息等,根据效果分为极好(J)、很好(A)、较好(B)、一般(C)、差(D)和很差(E)6种等级。客观统计主要利用平均梯度和熵。以下为具体的实验截图和记录。 第1组实验:空间域-直方图均衡,原始图像大小为1 024像素×1 024像素(见图2)。 图2 空间域-直方图均衡 由图2、表2可以看出,图像经直方图均衡之后会出现亮度过饱和现象。加入粗糙集约束之后,噪声明显减低,但同时丢失了图像中的部分细节。图像经本方法增强后,细节和轮廓凸现,对比度得到提升,质量明显改善。 表2 效果评价 第2组实验:频率域-同态滤波,原始图像大小为512像素×512像素(见图3)。 由图3、表3可知,原始红外热像仪得到的图像模糊,经同态滤波之后效果并没有得到改善。加入粗糙集约束之后,增强效果有了一定程度的改观。经本方法处理之后,图像的细节和边缘更为突出。 图3 频率域-同态滤波 表3 效果评价 由上述实验可以看出,加入改进的粗糙集约束之后,图像的平均梯度大体呈上升趋势,熵略为下降,因为噪声在一定程度上得到抑制,同时有选择地增强了潜在的图像细节和纹理。由于NSCT有着比小波变换更好的逼近效果,能更好地捕捉图像高频结构,因而其增强效果要优于基于小波变换的增强方法。实验证明,基于粗糙集的NSCT非线性增强方法效果较其它方法更为显著,图像经增强后大量的细节和纹理得到呈现,图像可识别的范围增大了,质量得到一定程度的提高。 本文分析了传统红外图像增强方法的优点和不足,提出了基于改进粗糙集和NSCT的红外遥感图像的增强,并进行了相关的图像质量评价,得出该算法相对于传统红外图像增强方法具有较好效果的结论。但是本算法中有些阈值的选择取决于人为判断,如何自适应地有效选取阈值将是下一步研究的重点。 [1]李俊山, 杨威, 张雄美. 红外图像处理、分析与融合[M]. 北京: 科学出版社, 2009 [2]赵耀宏, 史泽林, 罗海波, 等. 自适应红外图像直方图均衡增强算法[J]. 光电工程,2008,35(3): 97-101 [3]于天河, 戴景民. 基于多重分形的红外图像增强技术[J]. 红外与激光工程,2010,39(1): 184-188 [4]李建平, 杨万年.小波十讲[M].北京:国防工业出版社,2004 [5]成礼智, 王红霞, 罗永. 小波的理论和应用[M]. 北京:科学出版社, 2004 [6]程正兴, 杨守志, 冯晓霞. 小波分析的理论、算法、进展和应用[M]. 北京:国防工业出版社, 2007 [7]焦李成, 侯彪, 王爽, 等. 图像多尺度几何分析理论与应用[M]. 西安: 西安电子科技大学出版社, 2008 [8]闫敬文, 屈小波. 超小波分析及应用[M]. 北京:国防工业出版社, 2008 [9]Cunha L, Zhou J P, Do M N.The Nonsubsampled Contourlet Transform: Theory, Design, and Applications[J]. IEEE Transactions on Image Processing, 2006,15(10) [10]Pal S K, King R A. Image Enhancement Using Smoothing with Fuzzy Sets [J].IEEE Transaction on Sys Man Cybern,1981,11(7):494-501 [11]Guo M Z, Yang J L, Zhao J. Fuzzy Contrast Enhancement for Remote Sensing Image Based on Fuzzy Set in Nonsubsampled Contourlet Domain[C].Proc Ninth International Conference on Machine Learning and Cybernetics, 2010 [12]Pawlak Z. Rough Sets[J]. International Journal of Information and Computer Science, 1982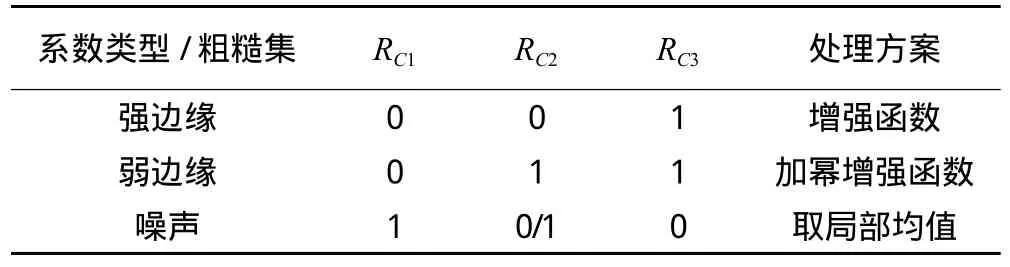
2.2 本文设计的算法
3 实验与分析

4 结 语

