基于卡尔曼滤波算法卫星数不足情况下的连续定位

谢 翔，郭际明，曹文涛，周命端

（1.武汉大学 测绘学院 精密工程与工业测量国家测绘局重点实验室，湖北 武汉 430079）

由于成本、硬件等原因，目前便携式GPS导航设备大多数都是使用伪距观测值。同时在城市中，由于大楼林立、树木遮挡等因素的影响，GPS接收机面临着信号弱、部分时刻卫星数不足等考验[1]。卡尔曼滤波模型广泛应用于动态导航定位领域，在分析其原理的基础上，本文提出了在卫星数不足4颗的情况下可采用卡尔曼滤波作为参数估计模型进行连续解算的方法。

1 卡尔曼滤波算法

1.1 基本卡尔曼滤波模型

一个有多个输入、输出量的离散时间线性动态系统，可用以下线性差分方程来表示其控制过程：

式中，u代表系统的输入向量，是一个可选项；x代表系统的状态向量；w代表过程噪声向量；A代表从tk-1到tk时刻的状态转移矩阵；B代表在tk-1时刻系统的输入向量与系统状态之间的关系矩阵。式（1）称为卡尔曼滤波的状态方程，描述了系统状态随时间变化的过程，是系统的动态模型。

卡尔曼滤波器假定系统的状态向量xk与其观测向量yk存在以下的线性关系：

式中，C代表观测量与系统状态之间的关系矩阵；vk代表了测量噪声向量。式（2）称为卡尔曼滤波的测量方程，其描述了当前系统测量值与系统状态之间的关系。

卡尔曼滤波假设向量wk中的每个过程噪声变量为一个期望为零的正态白噪声，即：

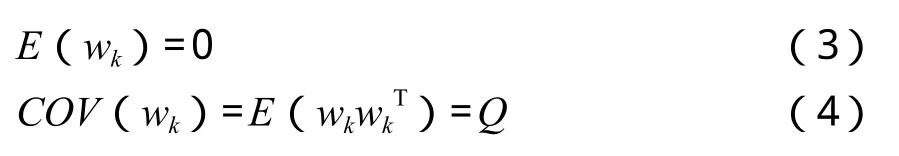
卡尔曼滤波假定每个测量噪声变量也是一个期望为零的正态白噪声，即：

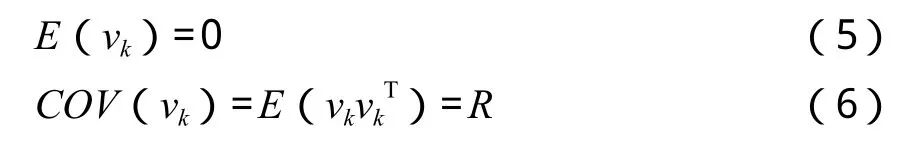
尽管测量噪声wk和vk的值是未知的，但它们的协方差矩阵Q和R对卡尔曼滤波来说是已知的。一般来说协方差阵Q和R会随着时间的不同而变化，但在这里为了简化公式，认定它们均是常系数矩阵。另外假定过程噪声向量wk中的各分量与测量噪声vk中的各分量互不相关，即：

式中，整数i和j均为任意有效历元[2]。

1.2 常用KF模型

1）静止用户：P模型。当接收机处于静止时，速度恒为0，只需把位置坐标和时钟作为系统状态，即x=［xpT,xcT］T。这里位置状态向量为xp=［x,y,z］T，时钟状态向量为xc=［b,d］T，b为本地钟差，d为本地钟漂。

2）低动态用户模型：PV模型。当用户处在一种低动态运动环境时，就应该采用PV模型。这种模型适用场合包括平稳驾驶的车船和步行者。在此模型中，速度分量被认为是随机游走过程。系统状态向量为x=［xpT,xvT,xcT］T，其中xvT=［vx,vy,vz］T，其余向量含义保持不变。本文中就采用这种模型。

3）高动态用户模型：PVA模型。在某些应用场合，用户的加速度变化较大，如飞机起降等，此时就需要将3个加速度分量加入系统状态向量中，这种模型就叫做PVA模型。系统向量为x=［xpT,xvT,xaT,xcT］T，xaT［ax,ay,az］T是新加进去的加速度状态向量[3]。

2 实例分析

2.1 卡尔曼滤波算法参数设置

本实例中采用了PV模型。在实际计算过程中，可以按照经验确定初始的方差矩阵，其中状态向量矩阵选择大一点，可以使滤波较快地收敛，初始方差矩阵见式（8）。

动态噪声矩阵Qk与历元无关，需要根据该动态模型的特性来确定，应该与动态模型的精度相匹配。如果Qk过大，则使得滤波在前一历元的观测值上加权过大，不能很好地利用当前观测值；如果过小，使滤波在前一历元的观测值上加权过小，随滤波的递推，将会引进越来越大的模型噪声，从而使滤波误差可能越来越大，甚至发散。在这里，选择的动态噪声矩阵如式（9）所示[4]。

2.2 动态数据分析

当运动载体经过高楼林立的街道等环境时，可能接收到的卫星不足4颗。此时，采用普通的最小二乘法无法正常解算，将造成一段时间内没有位置信息。卡尔曼滤波定位解算不仅依靠当前历元的观测值，也与前一历元的定位结果有关，因此可以考虑卡尔曼滤波在这种情况下的可行性。

选取1组车载动态数据，共4 000个历元，采样间隔0.1 s。首先采用普通最小二乘法进行伪距单点定位；再从第401个历元开始，连续对100个历元做如下处理：删除这些历元的部分观测值，即这段时间内每个历元参与解算的卫星数均小于4颗。采用卡尔曼滤波算法对处理后的观测值文件进行解算，将得到的2套空间三维坐标定位结果转换到空间大地坐标（B、L和H），如图1所示。左图原点位置为东经107.0599°，北纬25.0303°，右图为A区域局部放大图。

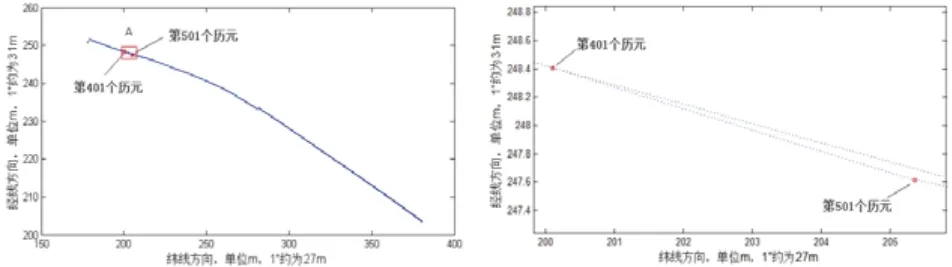
图1 处理前后运动轨迹点比较

从左图中可以看出，处理前后的运动轨迹基本重合，没有明显偏差。将A区域放大，看到从401个历元开始位置出现偏差，并且偏离的程度随着时间的增加越来越大，这是由于当前历元缺少足够的实际观测值进行修正，因此偏差增大。从第501个历元开始卫星数恢复正常，此时的状态估计值得到了实际测量值的修正，因而它的均方误差值变小，可靠性增加，运动轨迹逐渐恢复到正常轨迹上。

3 结 语

本文主要研究了在卫星数不足情况下利用卡尔曼滤波进行连续定位的方法，实验结果表明，随着时间的增加，精度会逐渐降低。但考虑到实际导航中，卫星数不足的历元为少数，且持续时间不会太长，因此本文研究内容具有一定的实用性。在进一步的研究中，可以考虑改进卡尔曼滤波算法，提高滤波器的动态性能，如自适应卡尔曼滤波算法、带渐消因子的优化算法及改进的优化算法等[5-7]，使其能适应复杂的导航条件。

[1]梁坤,施浒立,宁春林.室内环境中的GPS信号特性分析[J].天文研究与技术,2008,5(1):30-36

[2]谢钢. GPS原理与接收机设计[M].北京：电子工业出版社，2009

[3]鲁郁.GPS全球定位接收机——原理与软件实现[M].北京：电子工业出版社，2009

[4]祁芳.卡尔曼滤波算法在GPS非差相位精密单点定位中的应用研究[D].武汉：武汉大学，2003

[5]雷礼平.GPS动态卡尔曼滤波算法研究[D].成都：电子科技大学，2003

[6]郑利龙. 复杂环境下GPS信号参数估计与定位方法研究[D].北京：清华大学，2004

[7]胡国荣,欧吉坤. 改进的高动态GPS定位自适应卡尔曼滤波方法[J].测绘学报,1999(4): 290-294