基于矢量控制技术的同步电动机调速系统分析

饶 雪，何继光

（武汉大学 电气工程学院，湖北 武汉 430072）

矢量控制技术的采用，使同步电动机以特有的优点广泛应用在工业生产中，是工业生产中不可缺少的一种电机类型。矢量控制技术可以实现对同步电动机的动态控制，优化调速系统的性能。由于调节同步电动机的励磁可以改善电网的功率因数，所以大功率推进的场合常采用励磁可调的电励磁同步电动机，本文针对实际需求，对电励磁同步电动机的矢量控制展开研究。

1 同步电动机调速系统的发展及概述

纵观电气传动的发展过程，交、直流两大电气传动并存于各个业领域，虽然由于各个时期科学技术的发展使得它们所处的地位、所起的作用不同，但它们始终是随着工业技术的发展，特别是随着电力电子学和微电子学的发展，在相互竞争、相互促进中提高自身的性能，发生着变更。

同步电动机传动是交流电气传动的主要形式之一。最初的同步电动机只用于拖动恒速负载或用于改善功率因数的场合，上世纪30年代的后期，人们开始研究同步电动机的调速问题。尤其是有了半导体固态变流器后，采用逐渐升频起动的方法完全可以取代过去的一套起动装置，是一种很好的起动方法；同时，自控式调频则从根本上解决了振荡、失步问题。因此，同步电动机变频调速的应用范围越来越广阔。

2 矢量控制电动机原理的提出

2.1 矢量控制电动机基本原理

电动机调速的关键是转矩的控制。对于隐极同步电动机来说.其电磁转矩满足式Td=KmFrFSsinθrs，两个磁动势互不垂直，相互影响，要想控制好转矩，不但要控制好定、转子电流的幅值，还要控制好定、转子电流矢量之间的夹角，如用一般的方法，很难做到。另外，对于凸极转子的同步电动机来说，不仅存在着和隐极同步电功机相同的主电磁转矩，而且在定、转子之间还存在着由于凸极效应引起的磁阻转矩。因此，凸极同步电动机的转矩控制更加困难。

矢量变换控制理论的基本思想是在普通的三相交流电动机上设法模拟直流电动机转矩控制的规律，在磁场定向坐标上，将电流矢量分解成产生磁通的励磁电流分量和产生转矩的转矩电流分量，并使两分量相互垂直，彼此独立，然后分别进行调节。因此矢量控制的关键仍是对电流矢量的幅值和空间位置（频率和相位）的控制。

2.2 坐标系之间的矢量变换

矢量控制中所用坐标系有很多种，电动机的变量（电压、电流，电动势、磁链等）均可用空间矢量来描述，并常需要在几种坐标系中进行变换和计算。一个空间矢量从一种坐标系变换到另一种坐标系，需遵循下列规律[1]：

1）静止坐标系间的矢量变换：一个旋转矢量从三相定子坐标（R-S-T轴系）变换到子两相坐标系（α-β轴系），又称为3/2变换，其反变换称之为2/3变换。习惯上使α轴和A轴重合、空间矢量A由三相定子坐标系中的分量VR、VS、VT合成，如果在两相定子坐标系中的分量Vα、Vβ，合成后产生的矢量和A相等，那么，这种变换是等效的。三相到两相变换中的系数3/2及两相到三相逆变换中的系数2/3，是由于在变换过程中保持了旋转矢量幅值不变的结果。

2）矢量回转器：矢量回转器是矢量从一个直角坐标系到另一个直角坐标系的变换。这两个坐体系可以是旋转的，也可以是相对静止的。设矢量V存在于两个直角坐标系d-q和φ1-φ2中，矢量在d-q坐标系中的分量分别为Vd和Vq，在φ1-φ2坐标系中的分量分别为Vφ1和Vφ2，两个坐标系横轴夹角为φ。

3）矢量分析器（VA）：矢量分析器又称直角标到极坐标变换，用于求解一个矢量的模和相角，由于在实际电路中只用到相角的三角函数形式，因此，只求出相角的正弦值和余弦值即可。

2.3 凸极同步电动机的气隙磁链矢量定向控制

将定向坐标系的φ1轴与同步电动机的气隙磁链矢量V重合。实现气隙磁链定向控制[2]，如图1所示。

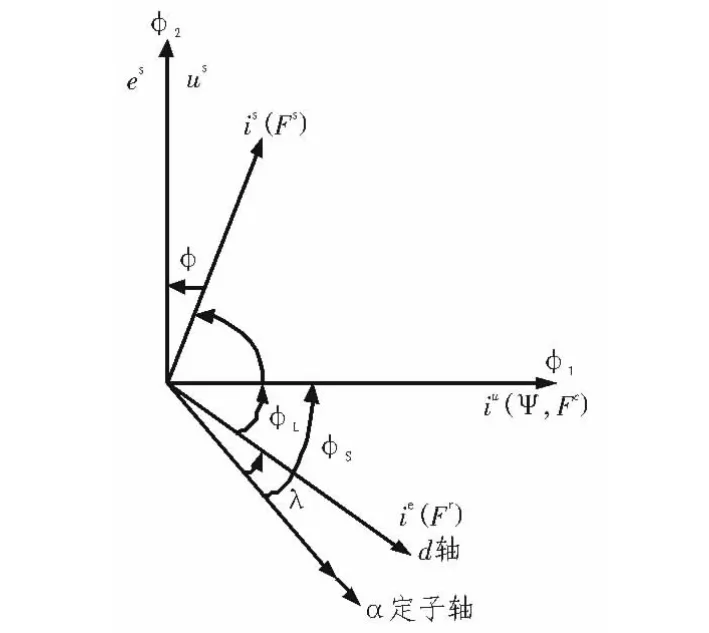
图1 励磁同步电动机矢量图Fig.1 Vector diagram of the excitation synchronous motor

在φ1-φ2坐标系，根据矢量控制原理，把有关矢量分解，气隙磁链是穿过气sφ1隙的主磁链，不包括定、转子漏磁链，因此：

由于ie和is按平行四边形法则合成，所以isφ2=-ieφ2有统一转矩公式，代入电流矢量和磁通矢量之间的关系式得同步电动机的转矩公式：

将其代入上式得：

式中Kms和Kms1是比例常数[3]。

上式说明，采用气隙磁链定向后，如果能够保持气隙磁链恒定，那么电磁转矩只与定子电流的转矩分量成正比。

同步电动机的转矩公式和直流电动机的转矩公式很相似，差别在于直流电动机中的转矩电流是物理上存在的电枢电流，而同步电动机的转矩电流是不直接存在的定子电流矢量在旋转坐标系轴上的直流分量。和直接电动机控制系统一样，isφ2的给定量is*φ2从速度调节器里获得。

从速度调节器和iφs*1=iφs*2tgφ得到了iφs*1和iφs*2，完成了计算被控矢量的直流控制分量。只要第二个变换（从φ1-φ2坐标系到R-S-T坐标系的坐标变换）就能得到物理上存在的定子三个电流的给定量usR、uss、usT。借助带电压前馈补偿的电流控制型交-交变频器，使定子电流的给定量的实际值等于它们的给定值，便完成了全部的矢量控制任务。其关键是找到坐标系变换所需的φ1轴和R轴之间的夹角φs－磁链位置角[4]。

3 电励磁同步电动机的矢量控制系统

有两种计算φs角的方法，本文主要介绍同步电动机的电流模型和电压模型[5]。

3.1 同步电动机的电流模型

利用定子电流磁化和转矩分量的给定量iφs*1和iφs*2，磁化电流的期望值iu*以及用于电动机轴上的位置发送器测的转子位置角λ，计算期望的磁链位置角φ*s，用φ*s代替φs进行坐标变换[6]。计算步骤如下：

2）利用矢量分析器，在φ1-φ2坐标系中计算矢量ie*的模和相位角φ*l。

ie*的计算公式为：

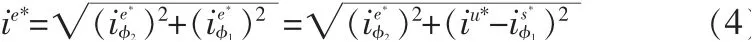
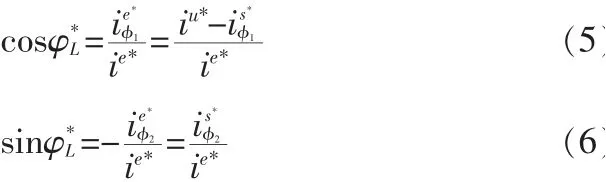
相角φ*的计算公式为：l式中，φ*l——φl的期望值；φl——从d轴到φ1轴的夹角。3）磁链位置角的期望值：

3.2 同步电动机的电压模型

对于磁链来说，它是一个开环控制系统，实际上在电流模型中，磁化曲线的模拟是粗糙的，由磁饱和及温度变化引起的电机参数的变化没有补偿，特别是同步电动机暂分量影响的忽略，带来有较大的误差，甚至使系统在高速时不能正常工作。采用磁链闭环控制可以克服上述缺点，为此需要一个测量磁链量ψ和位置角φs实际值的环节——电压模型。

电动机磁链矢量：

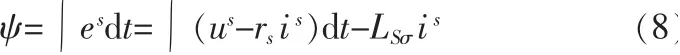
式中rs和LSσ——定子绕组电阻及漏感。

在α－β坐标系中：

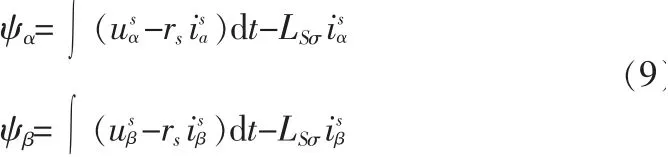
式（9）可用积分器实现[1]，积分回路中usα，usβ和isa，isβ，由电压、电流实际值信号usR、uss、usT和isR、isS、isT经3/2变换获得[7]。

该积分回路虽然简单，但存在下列问题：

第一，积分器初始值如何设定，这一问题可以在后面的论述中加以解决；

第二，积分器漂移如何抑制（数字积分器虽然无漂移，但存在误差积累），引入反馈通道能抑制漂移，可又出了如何保证积分精度问题；

第三，电机低速时，定子电动势很小，电压模型误差大，要求在低速时把电压模型及磁链闭环切除，靠电流模型工作，但存在如何实现平滑过渡问题。为解决上述问题，应该采取一定的解决措施，在原有电压模型的基础上，增加比例－积分反馈回路。

3.3 方案解决措施

F1（jω）和F2（jω）的对数频率特性由3个区域组成：

1）高频区——电压模型起主导作用；

2）低频区——电流模型起主导作用；

3）中频区——这是一个过渡区域。在额定角速度ω＝ωN时，工作点在高频区，磁链ψα＝∫esαd t由电压模型输出。随着电动机速度的下降，控制信号α按比例下降，工作点仍在高频区，这时电压模型起主导作用。当角速度ω＜ωB＝10%ωm（ωm为最高角速度）时，控制信号α迅速上升，工作点就从高频区转入低频区，这时电流模型起主导作用，这样既克服了低速时电压模型误差大的缺点，又可以使两种模型的切换实现平滑过渡。

因为电动机起动前，ω＝0，F1＝0，F2＝1输出ψα＝ω*α，所以积分器输出初始值被设定到电流模型输出值，通过这种方法，可以解决了第一个问题[8]。

把电压模型的输出ψα和ψβ送至矢量分析器VA，求模和幅角，得到磁链实际值信号ψ和磁链位置信号cosφs和sinφs，供定子电流控制及磁链闭环控制用。电流模型的输出ψ*α和ψ*β不直接参与控制，它们通过电压模型作用于系统。

4 结束语

气隙磁链定向矢量控制是针对普通同步电动机的难调速而发展起来的一种控制方法，是目前研究的热点，并在大功率的同步电动机交－交变频调速中的以应用。本文主要针对大功率的同步电动机进行了研究，主要作了以下几个方面的工作：

1）研究了矢量控制的基本理论，为实现电励磁同步电动机矢量控制做准备；

2）研究电励磁同步电动机的矢量控制策略，针对电压模型探讨其有缺点，并研究解决方案。

[1]马小亮.大功率交－交变频调速及矢量控制技术[M].北京：机械工业出版，2003.

[2]陈伯时.电力拖动控制系统[M].北京：机械工业出版社，2000.

[3]马志云.电机瞬态分析[M].北京：中国电力出版社，1996.

[4]陈坚.交流电机数学模型及调速系统[M].北京：国防工业出版社，1995.

[5]顾绳谷.电机及拖动基础[M].北京：机械工业出版社，1998.

[6]李宏民，朱展宇.同步电动机的电流模型和电压模型[J].马钢技术，1997：19－21.LI Hong-min，ZHU Zhan-yu.The current model and voltage model of synchronous motor[J].Maanshan Iron and Steel Technology，1997：19－21.

[7]胡崇岳.现代交流调速技术[M].北京：机械工业出版社，1995.

[8]陈伯时.变频调速系统[M].北京：机械工业出版社，1997.