基于结构方程模型的河北省企业技术创新能力评价

张立华

(河北联合大学经济学院，河北唐山063009)

进入21世纪以来，随着世界经济全球化进程的加快，各国各地区在经济领域的竞争越来越表现为以知识为基础的技术创新能力的竞争。面对机遇与挑战，各地如何尽快提升自己的区域技术创新能力已成为推动区域经济增长的主要因素和提高区域综合竞争力的核心问题。为此，笔者利用系统科学理论，通过建立区域技术创新能力评价系统，深入剖析了河北省区域技术创新能力的现状，提出了提升区域技术创新能力的对策。

一、区域技术创新的含义

区域技术创新能力是指在一个区域范围内，以增强区域经济增长的原动力为目标，充分发挥区域技术创新的行为组织，包括企业、高校及研究机构、科技中介服务及金融机构、政府等的技术创新积极性，以人力资本集聚为核心，高效配置技术创新资源，将技术创新构想转化为新产品、新工艺和新服务的综合能力系统。随着经济全球一体化趋势日益加深，区域技术创新能力逐步成为地区经济获得国际竞争优势的决定性因素。因此，全面评价和提升区域技术创新能力，对于促进地区经济发展，优化产业结构，有效配置区域内资源有着重要的意义。

表1 河北省区域创新能力评价指标体系

技术创新能力的培育，直接受制于多方面因素的影响。具体包括:知识生产能力、知识扩散能力、企业技术创新能力、创新环境、创新效益等五个方面的因素。本文将通过结构方程模型对影响河北省区域技术创新能力的各因素进行分析。

二、结构方程模型(SEM)概述

SEM中变量与变量之间的联结关系用结构参数表示，提供变量间因果关系不变性的常数，描述观测变量与观测变量之间，观测变量与潜在变量之间，以及潜在变量与潜在变量之间的关系［2］。这些变量又可归纳为两种模型，即测量模型和结构模型。

(一)测量模型(Measurement Model)也称为验证性因子分析模型，主要表示观测变量和潜变量之间的关系。度量模型一般由两个方程式组成，分别规定了内源潜在变量η和内源观测变量 y之间，以及外源潜在变量ξ和外源观测变量x之间的联系，模型形式为:

其中，x为外源观测变量组成的向量;Y为内源观测变量组成的向量;∧x为外源观测变量与外源潜在变量之间的关系，是外源观测变量在外源潜在变量上的因子负荷矩阵;∧y为内源观测变量与内源潜在变量之间的关系，是内源观测变量在内源潜在变量上的因子负荷矩阵;σ为外源观测变量x的误差;ε为内源观测变量y的误差;ξ与η分别是x与y的潜在变量。

(二)结构模式(Structural Equation Mode1)又称为潜变量因果关系模型，主要表示潜变量之间的关系。规定了所研究的系统中假设的外源潜在变量和内源潜在变量之间的因果关系，模型形式为:

其中，η是内源潜在变量;ξ是外源潜在变量;β是内源潜在变量η的系数矩阵，也是内源潜在变量间的通径系数矩阵;Γ是外生潜变量ξ的系数矩阵，也是外源潜在变量对相应内源潜在变量的通径系数矩阵;ζ为残差，是模型内未能解释的部分。

上述模型有以下一些假定:E(ζ)=0，E(σ)=0，E(ε)=0，E(ξ)=0，E(η)=0;ε与ζ相互独立，σ与ξ相互独立，ε与η相互独立，ζ、σ及ε相互独立。

三、河北省区域技术创新能力影响因素的综合分析

本文运用结构方程模型来分析区域技术创新能力评价中所涉及的不可直接测量的变量，基于结构方程本身的特性，需要设计调查问卷获取相关资料(此处由于篇幅限制，调查问卷具体内容省略)。《区域技术创新能力评价研究调查问卷》中的题项根据李克特量表法进行设计，采用受访者易于接受的5点评点法，依据影响区域技术创新能力的五个因素按照“完全不影响，“”影响不大、“有一定影响”、“有比较大的影响”、“完全影响”分别给予1、2、3、4、5 的评点。

本次调查问卷共发放200份，回收185份，问卷回收率问90.25%，除去填答残缺不全和存在明显矛盾重复的无效问卷后，有效问卷179分，有效问卷率为89.5%。

(一)信度与效度分析

在所有的研究中，在验证测量模型的过程中，主要进行问卷数据信度和效度的测试，以确保调查数据能够说明调查结论。

1．信度分析

数据的信度分析也就是数据的可靠性分析，是指一组计量项目是否在衡量同一概念，是衡量数据质量的一个重要的指标。本研究采用Cronbach’sα系数对其内部一致性信度进行测度，其结果见表2。

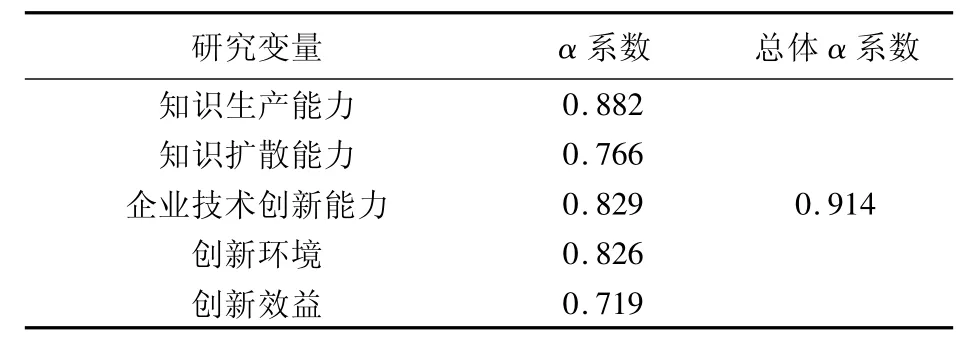
表2 克朗巴哈系数信度计算结果表

美国的统计学家海尔(Josep F．Hair Jr．)、安德森(Jr．Rolph E．Anderson)、泰(RonaldL．Tathan)和布莱克(Willian C．Blaek)指出:Cronbach’sα 值大于0．7，表明数据可靠性较高，计量尺度小于6时，Cronbach’sα 值大于 0．6，表明数据可靠的［3］。

从研究变量的信度检验表可以看出，这5个变量的 Cronbach’sα都在 0．7以上，而总量表为0.914，因此，可以认为各研究变量测量条款具有较高的内在一致性信度，调查数据是较为可靠的。

2．效度分析

效度(Validity)是指测量工具能正确测量出所要测量问题的程度，它是衡量调查问卷有效性的重要指标。本研究采用效标效度对测量工具的效度进行分析。校标分析的结果表明所有测量条目与总体的相关系数都在0.05水平上显著，证明测量工具的总体效度较好，详见表3。

表3 测量条目与总体样本的相关效度

3．模型研究假设

由于本研究提出的结构方程模型中的测量模型的信度和效度都已经得到了检验，因而，可以对结构模型进行分析。如前所述，知识生产能力、知识扩散能力、企业技术创新能力、创新环境和创新效益对区域技术创新能力产生一定的影响。所以，本研究提出以下假设:

假设H1:知识生产能力和区域技术创新能力之间存在正相关关系。知识生产能力越高，区域技术创新能力水平越高;反之，区域技术创新能力水平越低。

假设H2:知识扩散能力和区域技术创新能力之间存在正相关关系。知识扩散能力越强，区域技术创新能力水平越高;反之，区域技术创新能力水平越低。

假设H3:企业技术创新能力和区域技术创新能力之间存在正相关关系。企业技术创新能力越高，区域技术创新能力水平越高;反之，区域技术创新能力水平越低。

假设H4:创新环境和区域技术创新能力之间存在正相关关系。创新环境越好，区域技术创新能力水平越高;反之，区域技术创新能力水平越低。

假设H5:创新效益和区域技术创新能力之间存在正相关关系。创新效益越高，区域技术创新能力水平越高;反之，区域技术创新能力水平越低。

另一方面，一个区域的创新环境越好，企业技术创新能力和知识扩散能力越强，因此本文提出如下研究假设:

假设H6:创新环境与企业技术创新能力呈现正相关关系。

假设H7:创新环境和知识扩散能力呈现正相关关系。

模型中变量之间的关系可用通径图(图1)直观地表示，也可以利用结构方程金星表示，这两种方法是等价的。

图1 模型的可用通径图

本研究利用Amos7．0软件，进行结构方程分析以验证提出的假设。衡量结构方程模型拟合情况的拟合优度指数结果见表4。各类拟合指标均达到建议值，表明本研究提出的结构模型与实际数据拟合良好，可用于验证研究假设。各研究假设及其路径系数的统计检验结果如表5所示。

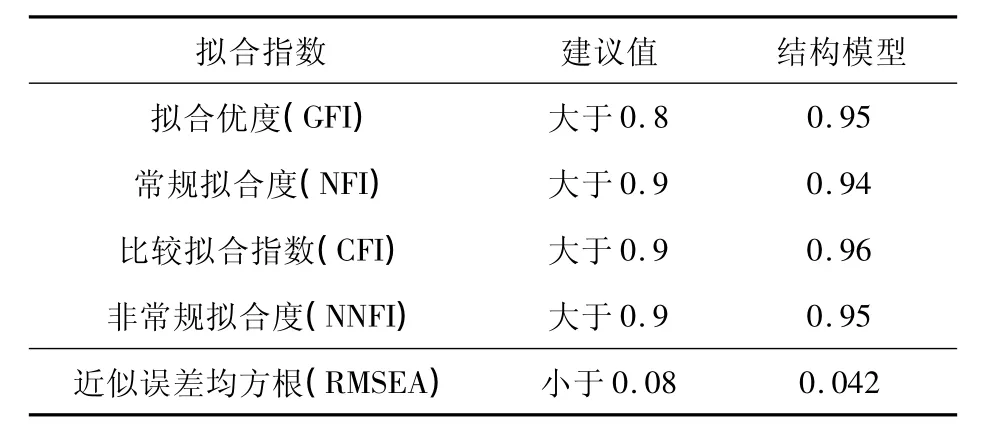
表4 结构模型拟合优度指数

表5 假设检验结果

从表5可以看出，知识生产能力和区域技术创新能力之间的路径系数是0.388，表明两者之间存在正相关关系，知识生产能力越强，区域技术创新能力越高;知识扩散能力和区域技术创新能力之间的路径系数为0.340，表明两者之间存在正相关关系，知识扩散能力越强，区域技术创新能力水平越高;企业技术创新能力和区域技术创新能力之间的路径系数为0.182，表明两者之间存在正相关关系，企业技术创新能力越高，区域技术创新能力水平越高;创新环境和区域技术创新能力之间的路径系数为0.109，表明两者之间存在正相关关系，创新环境越好，区域技术创新能力水平越高;创新效益和区域技术创新能力之间的路径系数为0.061，表明两者之间也存在正相关关系，创新效益越高，区域技术创新能力水平越高。

另外从表5可以看出，创新环境与企业技术创新能力之间的正相关关系，创新环境和知识扩散能力的正相关关系也被证实，综上，结构方程模型的模型假设都被证实，对区域技术创新能力影响评价具有重要的指导意义。

四、结 论

在研究区域技术创新能力个评价指标间相互关系的基础上，提出了区域技术创新能力评价的因果关系，利用结构方程模型进行评价模型的构建和求解实证研究显示，区域技术创新能力各评价指标之间并非相互独立而是相互影响、相互关联的，片面提高单个能力指标的水平并不一定能直接提升企区域技术创新能力，甚至可能适得其反。相反，把握各指标之间的相互影响与因果关系，准确定位关键指标和影响因素，才是有效增强企业技术创新能力的关键所在。因此，区域技术创新能力建设中，应当从知识生产能力、知识扩散能力、企业技术创新能力、创新环境和创新效益等五个方面同时着手，同时采取措施才能富有成效。

［1］ 易丹辉．结构方程模型方法与应用［M］．北京:中国人民大学出版社，2008．

［2］ 薛薇．SPSS统计分析方法及应用［M］．北京:电子工业出版社，2005:273-274．

［3］ 王国贞．河北省区域技术创新能力评价研究［J］．河北科技大学学报，2005，(2):30．

［4］ 史清琪，尚勇．中国产业技术创新能力研究［M］．北京:中国轻工业出版社，2000:2-23．

［5］ 张国良，陈宏民．国内外技术创新能力指数化评价比较分析［J］．系统工程理论方法应用．2006，15(5):385-392．

［6］ 李荣平，李建玲．产业技术创新能力评价方法研究［J］．河北科技大学学报，2003，24(1):13-18．