基于自抗扰控制器的电动变桨伺服控制技术研究

汪常明 ，张雷 ，胡书举 ，赵斌

（1.中国科学院 风能利用重点实验室，北京100190；2.中国科学院 电工研究所，北京 100190；3.中国科学院 研究生院，北京100049）

1 引言

随着全球能源的日益紧张，世界各国都在大力发展可再生能源。风能作为一种洁净的可再生能源已经得到了大规模开发应用。目前，国内外MW级以上风电机组已经成为风电市场主流机型，MW级以上风力发电机组普遍采用变桨距控制技术，变桨距伺服控制技术已经成为研究热点。

风电机组要求变桨系统具有位置无超调、动态响应速度快、稳定精度高和抗负载及参数扰动能力强等特点。在电动变桨伺服系统中，执行电机电枢绕组的电阻值和电感值易受温度影响，不同生产厂家提供的电机参数也存有差异，这些因素的影响会降低PID闭环控制系统性能。常规PID控制能够满足稳态精度高、动态响应快的要求，但在抗负载及电机参数扰动能力方面较差。为此，本文通过引入自抗扰控制器，可以很好地解决电机参数扰动带来的控制性能降低，同时可以解决快速性和超调的矛盾[1-2]，减小了转速超调对电动变桨齿轮箱的冲击。文中将自抗扰控制器应用于串励直流电机伺服控制系统的转速环，为满足电流跟踪的快速性，电流环采用传统PI控制方法。仿真结果表明，在串励直流电机电动变桨伺服系统中采用自抗扰控制技术，既控制住了较大范围内电机参数扰动或变化造成的不良影响，又实现了转速的快速无超调跟踪。

2 串励直流电机数学模型

串励直流电动机的电路原理图如图1所示。

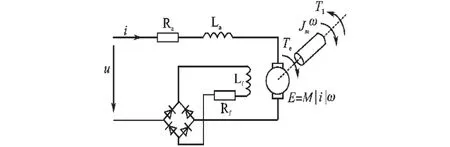
图1 串励直流电动机原理图Fig.1 Principle diagram of series-excited DC electrical motor

如果不计磁路磁通量的饱和，串励直流电动机的气隙磁通Φ与电枢电流和励磁电流If成正比，即Φ=kIf=k|Ia|，其中k为比例系数。电磁转矩与电枢电流之间的关系为Tem=CT·Φ·Ia，其中CT为转矩常数。从而可得串励直流电动机的电磁转矩方程为

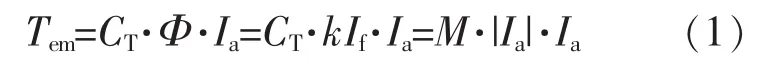
由式（1）可知，电动机电磁转矩正比于电枢电流的平方，即随着电流的增加，转矩将呈平方倍增加，所以串励电动机与其他类型的电动机相比，在启动电流一样的情况下，启动转矩较大，且过载能力也较强[3-4]。

根据图1，可以建立其动态电压平衡方程和转矩平衡方程为

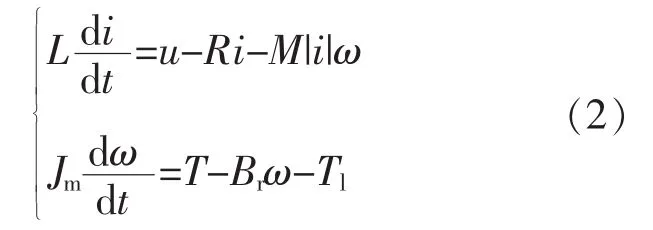
式中：i为电动机的电枢电流；ω为电动机的角速度；u为电动机的输入控制电压；R为电动机的电枢回路总电阻；L为电动机电枢回路总电感；Jm为电动机的转动惯量；Br为粘滞摩擦系数；T为电磁转矩，T=M|i|i；M为电动机转矩系数；Tl为负载转矩。

3 自抗扰控制器设计

自抗扰控制器（ADRC）是由韩京清研究员经过20多年的潜心研究提出的一种非线性控制器，具有系统响应快、超调小、参数适应范围广等优点，受到控制界的普遍关注，在电力、航空、电机调速系统等领域得到了推广应用[1，5-6]。

自抗扰控制器是由跟踪-微分器（TD）、扩张状态观测器（ESO）和误差非线性控制律（NLSEF）3 个部分构成的一种非线性控制器［5，7］。 首先，由TD跟踪输入信号及输入信号的微分；然后，与ESO反馈回来的被控对象的输出信号及输出信号的微分进行作差运算，在NLSEF中对误差反馈进行非线性控制；非线性控制的输出与ESO反馈回来的扰动量进行补偿，补偿后的控制信号最终作用到被控对象上。二阶自抗扰控制器的结构图如图2所示。

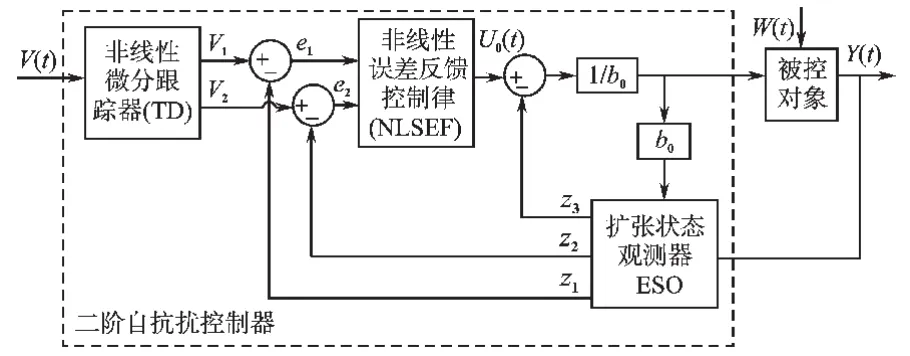
图2 二阶自抗扰控制器结构图Fig.2 Structure of a second order autodisturbances-rejection controller

自抗扰控制器吸收了经典PID控制器按反馈误差调节的精髓[7-8]，借鉴了状态观测的思想，并采用非线性组合来构造新型控制器。它克服了传统PID控制器通常无法获取微分信号的弱点，采用微分跟踪器来跟踪输入信号及其n阶微分信号，采用状态观测器跟踪输出信号及其n阶微分信号。通过使用扩张状态观测器对系统的总扰动（内扰和外扰）进行观测，然后对总扰动进行补偿，因而它不完全依赖于被控对象的数学模型。

下面给出二阶自抗扰控制器常用的离散控制算法。

跟踪-微分器TD为

式中：h为积分步长 （滤波参数）；r为决定跟踪快慢的参数；fst为离散时间系统最优函数。

算法中r和h为可调参数，r越大，跟踪速度越快，h越大，滤波效果越好。但是r和h又是一对矛盾，因此二者需要协调配合。

扩张状态观测器ESO为

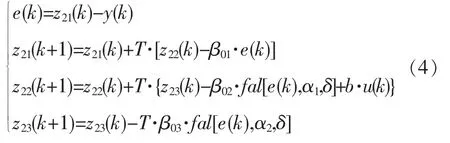
z21(k)，z22(k)为给出对象状态变量的估计，而z23(k)估计对象所有不确定模型和外扰的实时作用的总和，即 z23(k)→f(x1，x2，t)+w(t)。 非线性参数 α1，α2和δ一般根据实际运行经验取为固定值。β01，β02，β03是需要协调调整的参数。

非线性状态误差反馈控制律NLSEF为

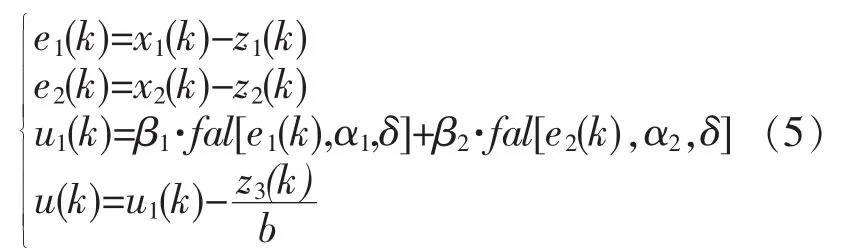
式中：x1(k)，x2(k)为由TD安排的过渡过程的输出及其微分；z1(k)，z2(k)和，z3(k)为由 ESO 输出的控制对象的状态变量；z3(k)/b是对扰动作用的补偿。

非线性参数{α1，α2，δ}一般根据实际运行经验取为固定值。系数β1，β2需要协调整定，适当增大参数β1，可加快响应速度，缩短过渡过程；适当增大参数β2，则可抑制超调。

式（4）和式（5）中的 fal（）函数的表达式为

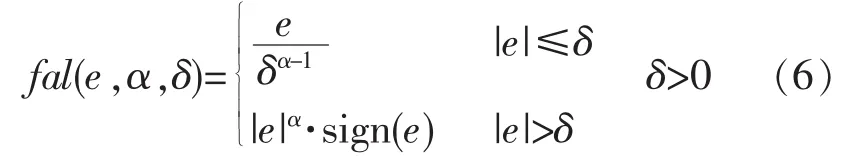
式中：e为误差值；δ和α为自抗扰控制器参数。

4 电动变桨伺服驱动转速环控制器设计及仿真验证

根据二阶自抗扰控制器TD，ESO及NLSEF 3个组成部分的离散控制算法，采用Matlab/Simulink中的S_Function函数来实现特殊动态系统定制成为用户自定义的Simulink模块［9-10］，按图2中的结构搭建二阶自抗扰控制器，其设计框图如图3所示。

图3 转速环二阶自抗扰控制器设计框图Fig.3 Design block diagram of the second order autodisturbances-rejection controller of speed ring

利用Matlab的封装技术对图3自抗扰控制器进行封装，将封装完的二阶自抗扰控制器应用于变桨伺服驱动系统的转速环，考虑到电流环对跟踪速度的要求，采用传统的PI控制器。其仿真系统结构如图4所示。

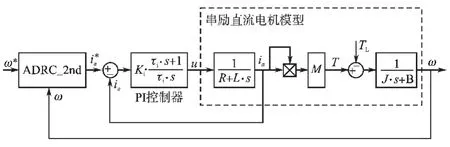
图4 伺服驱动系统仿真结构图Fig.4 Simulation structure of servo drive system

用于仿真的电机参数如下：电枢回路电阻0.273 4 Ω，电枢回路电感0.012 H，电动机的转动惯量 0.03 kg·m2，转矩系数 0.041 Wb/A，粘滞摩擦系数0.06。电机电枢绕组参数变化范围如表1所示，对比PI和ADRC控制算法的控制效果。

表1 电机电枢绕组参数变化表Tab.1 Motor armature winding parameters change table

仿真实验中，转速先给定为单位阶跃信号，等到响应稳定后，在0.2 s时转速给定阶跃至10 r/min，观察电机动态响应效果；然后，待电机重新稳定运行后，在0.6 s时负载转矩由初始值10 N·m跳变至20 N·m，观察转速和电流变化。

仿真结果如图5所示，图5中分别显示了不同参数下转速和电枢电流响应曲线。

图5 参数正常情况下响应曲线Fig.5 The response curves of parameter normally

参数正常情况下，分别调整好PI和ADRC的控制参数，跟踪单位阶跃时二者的控制效果基本一致。由图5可以看出，在0.2 s处，当转速阶跃跳变时，PI控制下的转速超调13%，而自抗扰控制下的转速无超调；在0.6 s处，转矩由10 N·m跳变至20 N·m时，ADRC控制下的转速变化也比PI控制下的效果优越。

由图6、图7可以看出，当电机参数扰动为50%，100%时，PI控制下初始的单位阶跃跟踪时转速跟踪变慢，电枢电流变化较大；而采用ADRC控制时，转速跟踪基本没有超调，电枢电流变化小。

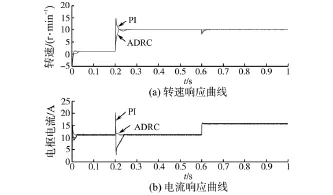
图6 参数增加50%时的响应曲线Fig.6 The response curves of parameters increased by 50%

图7 参数增加100%时的响应曲线Fig.7 The response curves of parameters increased by 100%

图8 参数增加200%时的响应曲线Fig.8 The response curves of parameters increased by 200%

从图8中可以看出，当电机参数增加200%时，PI控制情况下，转速超调达80%，电枢电流也变化剧烈，甚至出现负电流；而ADRC控制情况下，转速跟踪无超调，电枢电流超调2%。显而易见，采用ADRC较PID控制方法具有更好的控制效果。

5 结论

由Matlab仿真结果可以看到参数扰动情况下电动机的电枢电流、转速的变化过程，与常规的PID控制仿真结果相比，速度环采用自抗扰控制器不仅可以大大提高电机参数扰动的范围，而且可以既快又无超调的跟踪转速的给定值，具有良好的动态控制性能。由此证明了本文提出的电动变桨伺服控制方案的可行性，验证了自抗扰控制器参数适应性广，能自动检测并补偿控制对象内外扰动，在控制对象内部参数变动或遇到不确定性扰动时，都能得到很好的控制效果，具有较强的适应性和鲁棒性。

［1］韩京清.自抗扰控制器及其应用研究［J］.控制与决策，1998，13（1）：19-23.

［2］ZhengQing，ChenZhongzhou，GaoZhiqiang.APratical Approach to Disturbance Decoupling Control［J］.Control Engineering Practice， 2009，17（9）：1016-1025.

［3］陈伯时.电力拖动自动控制系统［M］.第3版.北京：机械工业出版社，2009.

［4］姚泽胜.电动汽车用串励直流电机控制原理的研究［D］.武汉：武汉理工大学，2011.

［5］韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术［M］.北京：国防工业出版社，2008.

［6］韩京清.从 PID 技术到“自抗扰控制”技术［J］.控制工程，2002，9（3）：13-18.

［7］Su J B，Qiu W B，Ma H Y，et al.Calibration-free Robotic Eye-hand Coordination Based on an Auto Disturbancerejection Controller［J］.IEEE Transactions on Robotics and Automation， 2004，20（5）：899-907.

［8］郭松山.电动机自抗扰控制技术研究综述［J］.机电技术，2009（S1）：12-15.

［9］王兵树，姜萍，林永君，等.SIMULINK中自抗扰控制技术自定义模块库的创建［J］. 系统仿真学报，2010，22（3）：610-615.

［10］胡琳静，孙政顺.SIMULINK中自定义模块的创建与封装［J］.控制工程，2008，15（S）：4-6.