PMSM伺服系统参数自整定研究

郑世祺，唐小琦，卢少武，宋宝

（华中科技大学 国家数控技术研究工程中心，湖北 武汉430074）

由于永磁同步电机具有系统响应快，速度高，运动平稳，传动效率高等特点，在数控机床中得到了广泛的应用。为了使永磁同步电机运行时充分发挥自身的优点，伺服系统的控制性能显得尤为重要。

PID参数是伺服系统中重要的控制参数，PID参数的好坏直接影响到伺服系统的控制性能，但是由于伺服系统的实际工作状态常常会发生改变，为了获得最优的伺服控制性能，就需要整定PID控制参数。 传统的PID整定方法Z-N法，临界比例法等，容易陷入局部最优，无法满足性能的要求[1]。

遗传算法是一种并行随机搜索最优方法，通过选择、交叉、变异这些遗传进化操作一步步地筛选出全局的最优解[2]。在系统辨识领域，最小二乘法由于其无需数理统计的知识，并且由其得到的估计具有最佳的统计特性，在工程中得到了广泛的应用。本文以永磁同步电机伺服系统为研究对象，有机结合实数遗传算法和递推最小二乘法对伺服系统参数进行自动整定。这种算法的特点是能够对给定范围内的参数值进行全局搜索，最后通过实验验证算法准确性。

1 永磁同步电机伺服系统数学模型

永磁同步电机伺服系统是一个耦合性较强的非线性系统，为了能够对系统进行良好的控制，必须从复杂的系统中抽象出其数学模型，达到系统设计的要求。

在伺服系统控制中通常采用id=0的控制方法，由电机学以及永磁同步电机的电磁模型可知，其电磁转矩可表示为

式中：Ψf为永磁体基波磁链；pn为磁极对数；iq分别为q轴电流。

在实际的机械运动中，考虑各种不同扰动力的作用，永磁同步电机的动力学方程可表示为

式中：J为电机转子及负载的总转动惯量；ωm为电机机械角速度；Tload为电机的负载转矩；Tf为摩擦转矩；Tcog为齿槽转矩；Tn为其他扰动转矩。

其中

式中：B为摩擦系数。

齿槽转矩可表示为

式中：An为常系数；Ψn为相应的处相角；h为电机的轴向长度。

综合式（1）～式（4）可得：

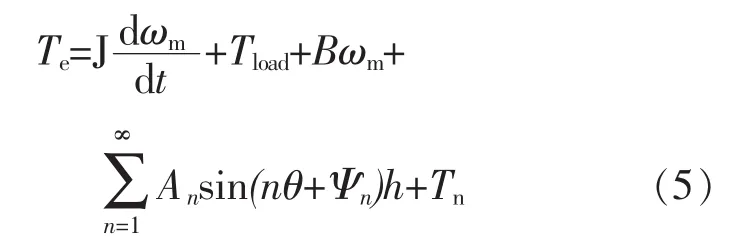
伺服系统普遍采用三环控制方法，即位置环、速度环和电流环，电流环属于内环，性能较好，其控制结构可等效为1/（Tds+1），Td为电流环时间常数，而速度环的控制参数整定是伺服系统参数整定的关键环节[3]。综合上述分析可以得到永磁同步电机伺服系统速度环控制器结构如图1所示。

图1 速度环控制器结构Fig.1 Structure of speed loop controller

图1 中的扰动为式（5）中的（Tload+Bωm+部分，对于虚线框中的模型，简化扰动部分的影响，可以整体近似为二价模型进行系统辨识。

被控对象的线性模型如下：

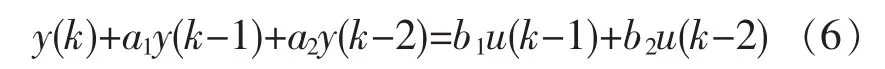
式中：a1，a2，b1，b2为需要辨识的参数，与电机结构及具体工况相关。

2 基于递推最小二乘法的系统辨识

对于上述速度环控制器的参数自整定，首先需要得到被控对象的数学模型，这里可以通过系统已知的参数，经过数学分析得到理想的数学模型，但是由于伺服系统工作的环境千差万别，伺服系统中各个环节的参数很难直接得到，而且伺服系统中各个因素互相耦合，数学分析得来的模型并不准确，为了能够自动调整伺服系统参数，就需要对被控对象进行系统辨识[4-5]。

由被控对象的线性模型可建立出可估计的预测模型表达式：

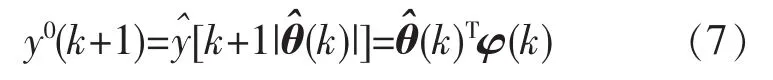
式中：y0(k+1)为 k+1 时刻的预测值为未知的参数向量；φ（k）为对应的输入输出数据向量。

并且有

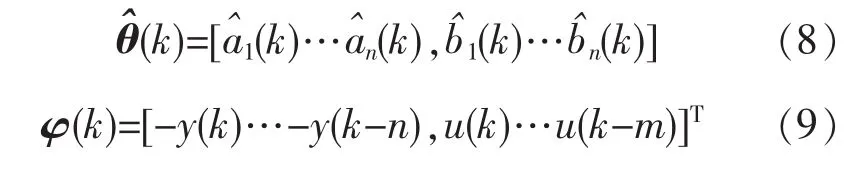
最小二乘法估计的准则是保证偏差的平方和最小即：

递推最小二乘法相比一般的最小二乘法，在工程上更易实现，其思想是沿着误差准则减小最快的方向，通过一步步的递推使误差准则最终达到系统辨识的要求。可归纳出其辨识的一般步骤。

1）确定增益矩阵K0和遗忘因子α。

K（0）通常由下式确定

遗忘因子通常有定常和时变两种取法即

或者

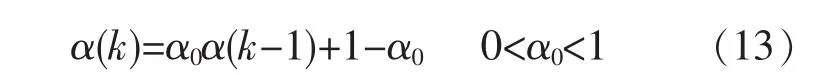
2）根据下式求出增益矩阵K（k）

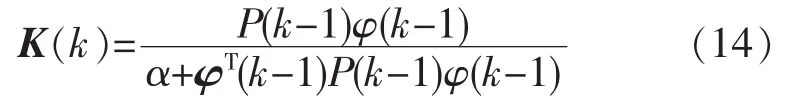
3）由增益矩阵 K（k）和下式可以递推出θ＾(k)的下一步估计值：

4）根据新得到参数估计值重新计算协方差矩阵 P（k）

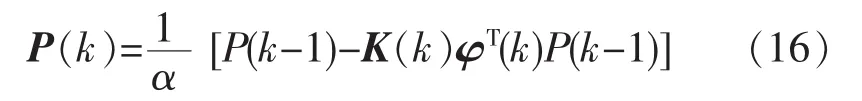
5）重新返回2）进行计算。

3 基于遗传算法的参数自整定

与一般的二进制编码遗传算法相比，实数编码遗传算法有许多优势，通过对解的实数表达，较二进制编码而言提高了算法的精度减少了存储空间，并且利用实数表示个体使得算法具有实际的物理意义，因此在对于复杂高维问题的求解上有着显著的优势。

1）初始种群。初始的种群个体代表的是需要寻优的参数，在对伺服电机PID控制参数（Kp，Ki，Kd）进行整定的过程中，Kd的引入可能造成整体系统的不稳定和震荡，所以只对Kp和Ki进行寻优。即参数优化向量可表示为

初始种群时随机产生N个均匀分布的个体。

2）适应度函数。在选取个体适应函数时，应该选取能够反映伺服系统性能的指标，这里选取系统偏差积分性能指标，这类指标包括ISE，ITSE，IAE，TAE[3]等。

ITAE能够得到优良的控制参数，阶跃响应的震荡较小，但是此类指标对于响应的超调没有考虑充分，因此在性能指标中加入超调量的影响，得到改进后的性能指标：

式中：w为惩罚因子。

3）选择算子。采用随机普遍取样来决定个体是否能够存在于后一代，具体操作时在当前种群及所有后代中，根据个体适应度从小到大排列，选取前N-N1个个体，然后再随机产生N1个个体，两部分集合到一起成为下一代种群。

4）交叉算子。利用交叉概率Pc随机选取两个父代个体，记作通过下式产生新的后代个体

5）变异算子。当个体进行完交叉操作之后，变异算子决定其是否需要进行变异操作。在实数编码遗传操作中，通过随机改变和产生新的基因信息来达到变异操作的目的。这里采用下式来进行：

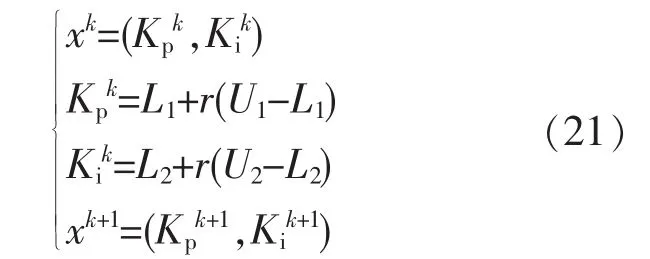
式中:xk为种群中变异前的个体；xk+1为个体经过变异操作后的新个体；L1，L2，U1，U2分别为 Kp，Ki参数的上下限；r为变异操作时产生的随机数。

6）终止规则。当进化代数达到所设定代数时，遗传终止，此时产生的解作为全局最优解。

4 永磁同步电机伺服系统参数自整定

最小二乘法能够快速准确地辨识出被控对象的数学模型，遗传算法能够在全局范围内找到满足要求的最优解，有机地结合上述两种方法，并根据直线电机的数学模型，能够得出针对永磁同步直线电机伺服系统的参数自整定方法。图2是针对伺服系统速度环参数自整定的整体结构图，根据图2归纳出自整定的基本步骤。

图2 永磁同步电机伺服系统速度环参数自整定Fig.2 Parameters auto-tuning of servo system of PMSM

Step1：使伺服系统速度环处于开环状态，给速度环被控对象施加激励信号，如伪随机数，扫频信号等，采集响应信号，由此得到数据点对样本

Step2： 由式（6）获得直线电机数学模型表达式。由式（8）、式（9）设

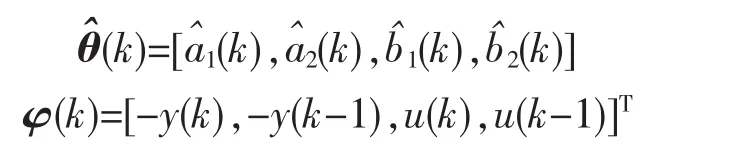
根据式（11）～式（16）及采集到的数据点对样本利用递推最小二乘法辨识出直线电机的数学模型。

Step3：把辨识出的数学模型替代原速度环被控对象进行PID控制，根据遗传算法初始化种群个体，即利用式（17）～式（21）进行遗传操作，最终得到优化的参数。

Step4：校验整定出的控制参数，若其作用下的速度闭环阶跃响应快速、稳定，则认为参数整定结果满足速度环控制整定的要求，自动整定过程结束，否则，返回Step1，重新进行整定。

5 实验研究

上述算法在永磁同步电机伺服系统中进行了验证，图3是实验平台的总体结构。

图3 实验平台结构Fig.3 Structure of experimental platform

实验中上位机运行运动控制软件，驱动PCI运动控制卡与伺服驱动进行通信，伺服驱动具有针对伺服电机的三环控制结构，驱动永磁同步电机运动。控制信号由上位机中的运动控制软件产生，电机的反馈信号由细分盒细分，传入伺服驱动，进而由上位机运动控制软件读取。通过这样一套实验平台不仅可以控制电机的运行而且可以方便地监测电机运行过程中的各个信号。

伺服系统采用TMS320F2812为核心控制器，电机额定电流I=8.3 A，伺服驱动器额定电流I=9.9 A，遗传算法中样本个体为30，交叉概率和变异概率为：Pc=0.9，Pm=0.033，惩罚因子选为 w=100，Kp的范围为 0～5，Ki的范围为 0～0.1。经过200代进化，得到Kp=4.821 7，Ki=0.006 9。代价函数J=15 063。代价函数J的优化过程如图4所示。

图4 代价函数J的优化过程Fig.4 The optimization process of the cost function J

把整定出的控制参数和最初的伺服出厂的经验值进行比较。图5、图6是伺服系统在正弦信号作用下输出的结果。可以看出，整定后伺服系统超调量较小，并且上升时间短，伺服系统具有优良的控制性能，参数整定达到了预期的效果。

图5 优化前PID控制输出Fig.5 PID control output before optimizing

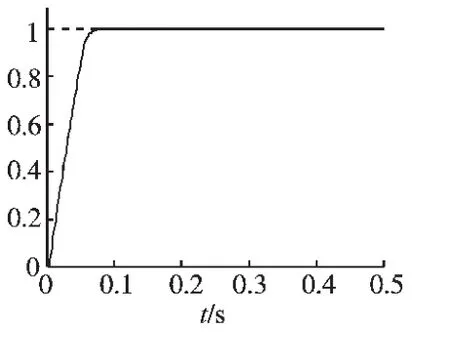
图6 优化后PID控制输出 Fig.6 PID control output after optimizing

进一步把多次实验整定出的PID参数和最初的PID经验值作比较，见表1，从表1中可以看出每次整定的结果与经验值相差较小，从而说明算法具有较强的稳定性与正确性。

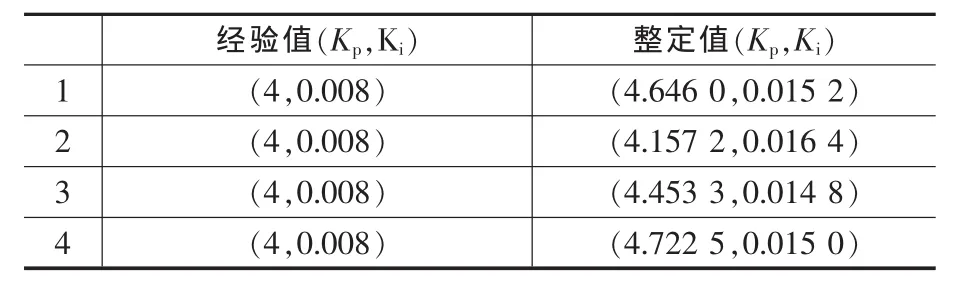
表1 PID经验值和整定值的比较Tab.1 Comparison on experienced PID value and tuned PID value

对整定前后的直线电机伺服系统进行扫频测试，得到整定前后的频率响应曲线，见图7，可以看出，整定后的伺服系统频带较整定前有较大的提高，说明整定后伺服系统的性能得到了较大的提高。

图7 整定前后的频率响应Fig.7 Frequency response before and after tuning

6 结论

本文首先建立了永磁同步电机伺服系统的数学模型，在此基础上对参数自整定进行了研究，综合最小二乘法和遗传算法的各自优点对伺服系统控制器参数进行了自动整定，最后通过实验对整定后的控制参数进行了验证，实验说明伺服系统整定后具有优良的控制性能，同时也证实了此算法的稳定性和正确性。

［2］陈彦桥，倪敏.实数编码的遗传算法在厂级负荷优化分配中的应用［J］.中国电机工程学报， 2007， 27（20）：107-112.

［3］陈鹏展，唐小琦，任清荣.基于IITAE评价指标的交流伺服系统参数自动整定［J］.微电机，2010， 43（2）：70-73.

［4］卢少武，唐小琦，宋宝.伺服系统转动惯量辨识及其应用［J］.微电机， 2011， 44（10）：41-43.

［5］XIONG Weiwei，YIN Chengliang，ZHANG Yong，et al.SeriesparallelHybridVehicleControlStrategyDesignandOptimization Using Real-valued Genetic Algorithm ［J］.Chinese Journal of Mechanical Engineering， 2009， 22（6）：862-868.