一种基于无速度传感器的PMSM的转子角度、转速估计方法

周宏林，况明伟，吴建东

（中国东方电气集团有限公司 中央研究院，四川 成都611731）

1 引言

永磁同步电机因其结构紧凑、性能可靠而在风力发电、电动汽车、船舶驱动等领域得到了广泛的应用。为了完成永磁同步电机的控制，需要获取其转子的角度和转速。采用角度和转速传感器来获取这一信息是一种直接的方式。然而在很多应用中，安装角度和转速传感器不仅增加了安装、维护成本，也使系统易受外部环境干扰，降低了系统的可靠性。而基于无速度传感器的永磁同步电机的转子角度、转速估计方法只需检测电机的定子电流、电压，结合电机的模型，即可从中提取转子的角度、转速信息，从而省去角度和转速传感器，达到提高系统可靠性，降低成本的目的。典型的永磁同步电机驱动系统如图1所示。

目前基于无速度传感器的永磁同步电机的转子角度、转速估计方法主要分为2类。一类是基于状态观测器或扩展卡尔曼滤波的方法[1-2]，这类方法将定子电流、转子角度和转速视为状态变量，然后采用传统的观测器或扩展卡尔曼滤波器方法进行观测。但由于算法较为复杂且负载转矩未知，这类方法的实际应用效果不够理想[3]。另一类是基于反电动势的估计方法[4-7]，例如滑模观测器[6]、反电势锁相环 （EMF phase-locked loop）法[7]等。其中，反电势锁相环法物理概念较为清晰，实现较为简单，因而得到了较为广泛的应用。但由于引入了锁相环，因此这类估计方法动态特性将会降低。当角度、转速估计模块和永磁同步电机的前向控制通道形成闭环后，位于反馈通道上的角度、转速估计模块的慢动态特性会使得整个系统的动态性能下降，甚至导致系统的不稳定。

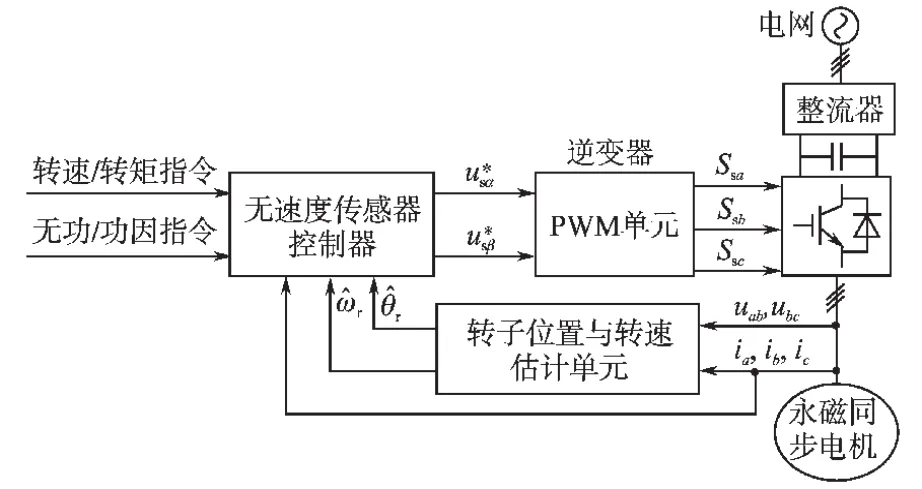
图1 永磁同步电机控制系统典型结构Fig.1 Typical structure of PMSM control system

为提高估计方法的动态特性，提出一种新的转子角度、转速估计方法。和传统估计方法直接估计转子角度不同，该方法首先引入转子磁链信息来估计转子初始角度，然后再将其结果叠加到转子角度计算值上，最终获得转子角度的无偏估计。由此能够在消除锁相环的同时避免可能引起闭环控制系统不稳定的局部环。由于该方法只需要进行前向通道的计算，估计方法的动态特性能够得到有效提高。

本文将首先简要介绍永磁同步电机在定子参考系下的模型。然后基于此模型提出转子角度和转速估计方法。最后将该方法应用于典型的1.5 MW直驱风力发电系统中，并通过Matlab/Simulink仿真对其性能进行评估。

2 静止坐标系下的永磁同步电机模型

根据永磁同步电机在转子旋转坐标系下的数学模型不难推导得到在静止坐标系下的永磁同步电机的数学模型（电动机惯例）：

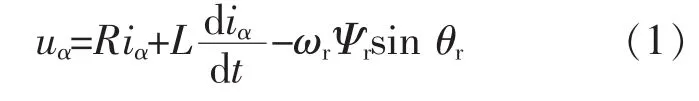
式中：uα，uβ，iα，iβ分别为定子电压和电流在 α，β 坐标系下的分量；θr，ωr分别为转子的电角度和电转速；Ψr为转子磁链的幅值；R，L分别为定子电阻和电抗。

根据上述模型可知定子侧的反电动势为

可以看出，α，β坐标系下的反电动势空间矢量的幅值与转子转速成正比，角度则反映了转子的角度。通过对反电动势空间矢量的估计就能够获得转子角度和转速的信息。

3 静止坐标系下的定子反电动势估计

由式（3）、式（4）可知，为了估计定子反电动势首先需要估计定子电流的微分值。这里提出采用高通滤波器的估计方法，因为高通滤波器可以引入90°的超前相位。需要注意的是，增加高通滤波器带宽能够提高基波分量的估计精度，但同时会放大定子电流中的PWM谐波。因此，建议采用时间常数τ在TPWM和2TPWM之间的一阶高通滤波器（TPWM为PWM周期）。于是定子电流微分估计值可以表示为

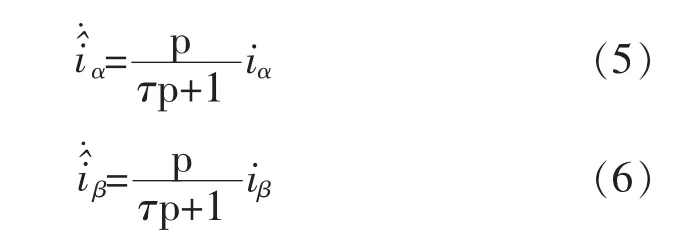
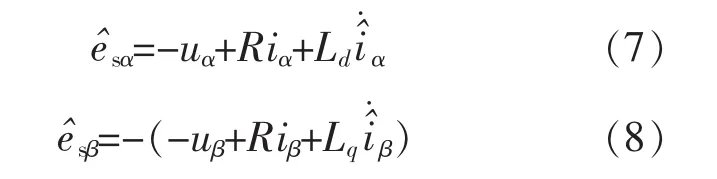
4 转子角度和转速的估计

获得反电动势估计值后，由式（3）、式（4）不难进一步得到转子转速和角度的计算值：

完整的实现框图如图2所示。

图2 转子角度、转速估计方法的实现框图Fig.2 Implementation block diagram of the rotor position and estimation method

在实际应用中，尤其是大容量驱动场合下，转速ωr变化相对较为缓慢，无速度传感器控制对转速估计动态特性的要求并不太高，因此，式（11）直接对转子转速计算值进行低通滤波来获得转子转速估计值相反的，由于转子角度θr，变化较快，因此无速度传感器控制对转子角度估计的动态特性有较高的要求，如果直接对转子角度计算值进行低通滤波，引入的相位延迟将导致闭环系统不稳定。为此，式(13)采用对缓慢变化的转子初始角度计算值进行滤波来获取转子初始角度估计值这样即可减小相位延迟带来的影响。然后通过式(12)将转子初始角度估计值叠加到有偏转子角度计算值上，最终形成转子角度的无偏估计值。由此可以看出，所提出的估计方法在成功消除局部环的同时保证了转子角度估计的快速性。

此外，由式(11)～式(13)还可以看出，该方法只有2个低通滤波器的时间常数参数需要整定，且二者相互独立，调试简单，易于工程实践。

5 仿真实验结果

为验证所提出估计方法的有效性，将其应用于基于典型的1.5 MW永磁同步电机的直驱式风力发电系统中，如图 1所示。直驱风力发电机组的参数为：额定电压UN=690 V，额定频率fN=11.5 Hz，定子电阻=3.0 mΩ，直轴电抗 Ld=2.9 mH，交轴电抗Lq=2.9 mH，PWM频率fPWM=2 kHz。

上述估计方法中，高通滤波器时间常数τ选择为2TPWM=1.0×10-3s，低通滤波器LP1和LP2设计为时间常数分别为0.02 s和0.01 s的一阶低通滤波器。仿真在无速度传感器控制的闭环条件下完成，其中无速度传感器采用有功/无功控制方式，并假设风力机运行在转速模式。

初始时，发电机空载，并运行于额定转速。为评估所提出估计方法的动态特性，转子角度初始值设置为-π/2，同时在t=0.2 s时为风力机施加一个-0.1（标幺值）的转速阶跃。仿真结果如图 3所示。作为对比，图 4也给出了传统反电势锁相环估计方法的结果。可以看出，两种估计方法最终都能够收敛到转速、转角实际值上。对转速估计，两种方法的收敛速度基本相同；但对转子角度估计，两种方法的收敛过程存在差异且所提出的方法收敛更快。在传统反电势锁相环估计方法中，由于锁相环存在动态调节过程，因此其角度估计值先减小再增大，跟踪延迟较大。而在所提出的方法中，由于避免了锁相环，角度估计值能够直接跟踪实际值，从而具有更快的动态特性。

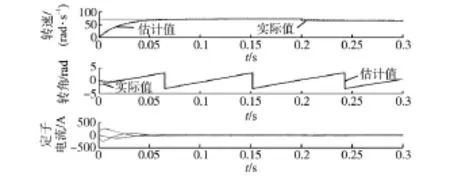
图3 所提出估计方法的仿真结果Fig.3 Simulation results of the proposed estimated method

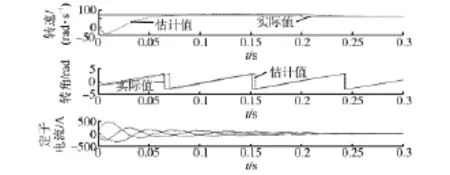
图4 反电势锁相环方法的仿真结果Fig.4 Simulation results of the EPLL method

为进一步验证所提出的估计方法在带载情况下的性能，设定从t=0.35 s开始，有功功率指令斜坡上升直到在t=0.48 s时达到1.0（标幺值）。类似的，还在t=0.5 s处为风力机施加0.1（标幺值）的转速阶跃用于验证动态特性，对比所提出方法和传统反电势锁相环方法的仿真结果如图5和图 6所示。可以看出，在永磁同步发电机带载的情况下，所提出方法的稳态精度略有下降（误差约2%），但其动态性能仍然优于传统反电势锁相环方法。

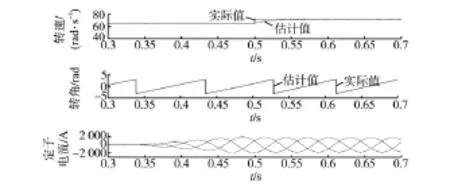
图5 所提出估计方法的仿真结果Fig.5 Simulation results of the proposed estimated method

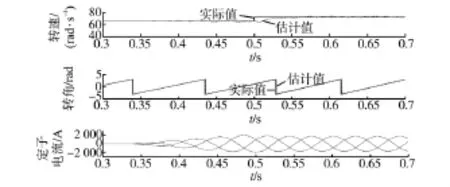
图6 反电势锁相环方法的仿真结果Fig.6 Simulation results of the EPLL method

6 结论

针对基于无速度传感器的永磁同步电机，本文提出了一种新的转子角度、转速估计方法。该方法基于静止坐标系对永磁同步电机的转子进行角度、转速估计，可以在避免传统估计方案中基于锁相环的转子磁链定向过程的同时，消除可能引起系统不稳定的局部环，进而提高估计方法的动态性能。为获得转子角度估计值，该方法并不直接对快速变化的转子角度计算值θcr进行滤波，而是首先对缓慢变化的转子角度初值θcr0进行滤波，获得其估计值θ＾r0，然后再将其叠加到快速变化的有偏转子角度计算值上，从而获得转子角度的无偏估计。针对典型的1.5 MW直驱风力发电系统的仿真实验结果显示，该估计方法的稳态特性与传统反电势法类似，但动态特性得到了显著的提高。

［1］González L G，Figueres E，Garcerá G，et al.Synchronization Techniques Comparison for Sensorless Control Applied to Wind Energy Conversion Systems［C］∥ EPE2009.13th European Conf.on Power Electronics and Applications，2009：1-9.

［2］Boussak M.Digital Signal Processor Based Sensorless Speed Control of a Permanent Magnet Synchronous Motor Drive Using Extended Kalman Filter［J］.EPE J.，2001，11（3）： 7-15.

［3］Li L，Geng H，Yang G，et al.Comparisons of Four Rotor Speed Identification Schemesfor PMSG Based WECS ［C］∥ ICEMS 2011， Beijing，2011：1-6.

［4］Chen Z，Tomita M,Doki S， et al.An Extended Electromotive Force Model for Sensorless Control of Interior Permanent Magnet Synchronous Motors［J］.IEEE Trans.Ind.Electron.，2003,50（2）:288-295.

［5］Kim H，Harke M C，Lorenz R D.Sensorless Control of Interior Permanent-magnet Machine Drives with Zero Phase Lag Position Estimation［J］.IEEE Trans.Ind.Appl.， 2003,39（6）：1726-1733.

［6］Kittithuch P,Mongkol K.Speed Sensorless Control of PMSM Using an Improved Sliding Mode Observer with Sigmoid Function［J］.ECTI Transactions on Electrical ENG.， Electronic， and Communications，2007,5（1）:51-55.

［7］Hu S，Xu H.Research on Sensorless Control Based Back toback Converter for Direct-driven WECS［C］∥Power and Energy Engineering Conference，2009.APPEEC 2009.Asia-Pacific，2009:1-4.