基于强化学习算法的双馈感应风力发电机自校正控制

李 靖，余 涛，王克英，唐 捷

(1.华南理工大学，广东广州510640;2.广东电网公司韶关供电局，广东韶关512026)

0 引 言

变速恒频双馈发电是目前风力发电普遍采用的一种发电方式，其发电机采用双馈感应电机［1］。当机组工作在额定风速以下时，通过调节发电机转子转速，保持最佳叶尖速比，实现对风能的最大捕获。其控制系统常采用基于定子磁场定向的矢量控制，实现发电机有功、无功功率的解耦控制。

由于风能具有强烈的随机性、时变性，且系统含有未建模或无法准确建模的动态部分，使双馈发电系统成为一个多变量、非线性、强耦合系统，因此仅采用传统矢量控制难以满足控制系统对高适应性和高鲁棒性的要求［2］。文献［3］采用神经网络控制方案，改善了控制性能，但稳态误差较大。文献［4］提出了模糊滑模控制策略，将模糊控制和滑模控制相结合，取得了良好的控制效果，但实现较复杂。

本文提出一种基于强化学习的双馈风力发电机自校正控制策略。强化学习控制算法对被控对象的数学模型和运行状态不敏感，其自学习能力对参数变化或外部干扰具有较强的自适应性和鲁棒性。仿真结果表明，该自校正控制器能够快速自动地优化风机控制系统的输出，不仅实现了对风能的最大追踪，而且具有良好的动态性能，显著增强了控制系统的鲁棒性和适应性。

1 定子磁链定向矢量控制

当定子取发电机惯例、转子取电动机惯例时，三相对称系统中具有均匀气隙的双馈感应发电机在两相同步旋转dq坐标系下的数学模型:［5］

式中:下标d和q分别表示d轴和q轴分量;下标s和 r分别表示定子和转子分量;U、i、ψ、Te、P、Q 分别表示电压、电流、磁链、电磁转矩、有功和无功功率;R、L分别表示电阻和电感;ω1为同步转速;ωs为转差电角速度，ωs=ω1－ωr=sω1;ωr为发电机转子电角速度，s为转差率;p为极对数;p为微分算子。

采用定子磁链定向矢量控制，将定子磁链矢量定向于d轴上，有ψds=ψs，ψqs=0。稳态运行时，定子磁链保持恒定，忽略定子绕组电阻压降，则Uds=0，Uqs=ω1ψs=Us，Us为定子电压矢量幅值。

由式(6)得:

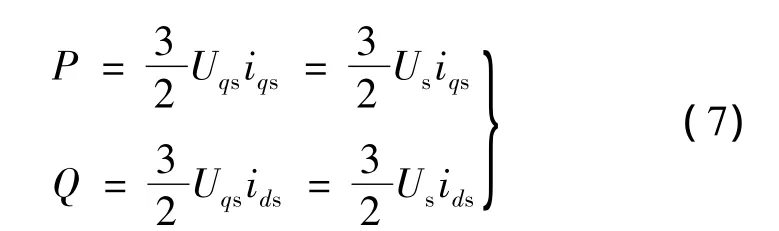
由式(3)得:

由式(4)得:

再由式(2)得:

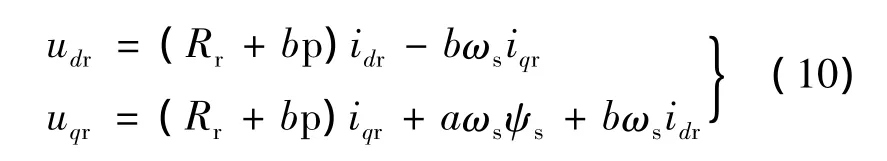
通过式(7)～式(10)可设计出双馈感应风力发电系统在定子磁链定向下的基于PI控制的矢量控制系统。

2 强化学习自校正控制器设计

2.1 强化学习算法原理

强化学习［6］(以下简称RL)是系统从环境状态到动作映射的学习，是一种试探评价的学习过程，可用图1来描述［7］。Agent根据学习算法选择一个动作作用于环境(即系统)，引起环境状态s的变化，环境再反馈一个立即强化信号(奖或罚)给Agent，A-gent根据强化信号及环境的新状态s'再选择下一个动作。近年来，RL理论在电力系统中用于调度、无功优化和电力市场等领域的应用研究成果显著［8］。

图1 强化学习系统

Q学习算法是一种从长期的观点通过试错与环境交互来改进控制策略的强化学习算法，其显著特点之一是对象模型的无关性［9］。通过优化一个可迭代计算的状态－动作对值函数Q(s，a)来在线求取最优控制策略。Tsitsiklis等人证明了Q学习算法的收敛性［10］。

Q学习的目的是估计最优控制策略的Q值。设Qk表示最优值函数Q*的第k次迭代值，Q值按迭代公式(11)更新［9］:

动作选择策略是Q学习控制算法的关键。定义Agent在状态s下选择具有最高Q值的动作称为贪婪策略p*，其动作称为贪婪动作。

若Agent每次迭代都选取Q值最高的动作，会导致收敛于局部最优，因为总是执行相同的动作链而未搜索其他动作。为避免这种情况，本文利用一种追踪算法［11］来设计动作选择策略。该算法基于概率分布，初始化时，赋予各状态下每个可行动作相等的被选概率，随着迭代的进行，概率随Q值表格的变化而变化，更新公式如下:

2.2 自校正控制器的结构

以固定增益的PI控制器构建的现有双馈感应风机控制系统，当系统工况改变时，控制性能会下降。而Q学习控制算法具有的对象模型无关性，以及对参数变化或外部干扰的自适应性和鲁棒性的特点，为改善风机的控制性能提供了一种思路。

本文提出一种自校正控制架构，如图2所示。在原PI控制器的基础上附加一个RL控制器，来动态校正PI控制器的输出，其中RL－P和RL－Q控制器分别对有功和无功功率控制信号校正。RL控制器在运行过程一直处于在线学习状态，被控量一旦偏离控制目标(比如参数变化或外部扰动所致)，便自动调整控制策略，从而增加原控制系统的自适应和自学习能力。

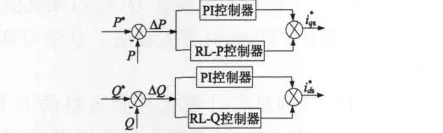
图2 双馈风力发电系统自校正控制框图

2.3 自校正控制器的设计

状态和动作空间的离散化是设计基于Q学习算法的风机自校正控制器的首要步骤也是关键之一。RL－P控制器的状态集合S包括(－∞，－0.1)、［－0.1，－0.06)、［－0.06，－0.03)、［－0.03，－0.02)、［－0.02，－0.005)、［－0.005，0.005］、(0.005，0.02］、(0.02，0.03］、(0.03，0.06］、(0.06，0.1］、(0.1，+ ∞)共 11 个不同状态;所允许的输出为离散动作集合 A，包括［0.06，0.04，0.03，0.02，0.01，0，－0.01，－0.02，－0.03，－ 0.04，－0.06］共11个动作值，被选择的动作与PI控制器的信号相叠加。RL－Q控制器的状态划分和允许离散动作集合与RL－P控制器相同。

第k步时刻的立即强化信号r由被控量的方差及带权值的相应动作变化量的平方之和组成，考虑到控制目标是使功率偏差尽可能小，故取其负值，即:

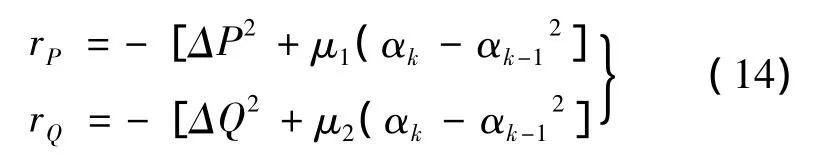
奖励函数中引入动作变化项是为了减少控制信号的波动，从而减少机械应力。式中αk值是动作集合A的指针，而不是实际的输出值，μ1和μ2为平衡前后各平方项的权重值。

在确定了状态集、动作集和奖励函数后，即可进行强化学习控制器在线自学习和动态优化。由于在最开始阶段缺乏经验，控制器需经历一段随机动作探索的预学习过程。此过程完成后，称其为PI/RL控制器，可投入实际系统参与运行控制。基于Q学习算法的自校正强化学习流程图如图3所示。

图3 自校正学习流程图

3 仿真结果与分析

为验证本文所设计的控制器的正确性和有效性，选择如下参数进行仿真验证:双馈风力发电机额定功率为P=6×1.5 MW=9 MW，=0.007，=0.005，=3.071，=3.056，=2.9，p=3。

3.1 无功功率调节

无功功率初始给定为0.9 Mvar，1 s时降为零，2 s后再次上升0.9 Mvar，3 s时仿真结束。仿真期间，保持风速为10 m/s不变，仿真结果如图4所示。由图4(a)可看出，基于强化学习算法的自校正控制动态性能优于传统矢量控制。图4(b)是强化学习控制器基于无功功率偏差输出的校正控制信号。由图4(c)可看出，在无功功率调节过程中，有功功率始终保持不变，很好地实现了解耦。

图4 无功功率调节过程系统响应

3.2 有功功率调节

风速初始给定为10 m/s，2 s时上升为11 m/s，30 s时仿真结束。仿真期间，设定无功功率为零，仿真结果如图5所示。由图5(a)可看出，基于强化学习算法的自校正控制和传统矢量控制有功功率响应曲线基本重合。这是因为基于最大风能捕获原理，当风速突变时，有功功率参考值不突变而是按照最佳功率曲线变化［13］，功率偏差始终很小，未达到强化学习设定最小动作值的状态，故强化学习控制器输出控制信号为零，从而两条曲线重合。由图5(c)可看出，在有功功率调节过程中，无功功率不受影响，实现了解耦。

图5 有功功率调节过程系统响应

3.3 扰动分析

图6 参数变化时动态响应

为考察系统对电机参数变化的鲁棒性，假设风速为10 m/s不变，在t=2 s时b增大一倍。图6给出了参数变化后，相同条件下传统矢量控制与基于强化学习算法的自校正控制的动态响应曲线。由图6(c)和图6(d)可看出，当参数变化导致有功和无功功率与参考值出现偏差后，强化学习控制器根据偏差值立即输出校正控制信号，来补偿参数变化的影响。由图6(a)和图6(b)可看出，采用自校正控制，超调较小，改善了动态品质，提高了控制性能。

4 结 语

双馈风力发电系统具有多变量、非线性、受参数变化和外部干扰显著的特点，利用强化学习算法具有的在线自学习能力和模型无关性特点，设计了风机自校正控制器，可有效提高其控制系统的鲁棒性和自适应性。此外，该控制策略无需改变原PI控制器的结构和参数，只需增加一个自校正模块，工程实现十分简便。同时，在研究中笔者发现，由于RL控制器的控制信号为离散动作值，易导致超调，后续研究中可考虑结合模糊控制对输入输出信号模糊化。

［1］刘吉宏，徐大平，吕跃刚.双馈感应发电机转速的非线性模型预测 控制［J］.电网技术，2011，35(4):159 －163.

［2］王君瑞，钟彦儒，宋卫章.基于无源性与自适应降阶观测器的双馈风力发电机控制［J］.中国电机工程学报，2011，31(33):159－168.

［3］Li H，Shi K L，Mclaren P G.Neural－ Network － Based Sensorless Maximum Wind Energy Capture with Compensated Power Coefficient［J］.IEEE Transactions on Industry Applications，2005，41(6):1548－1556.

［4］孔屹刚，王志新.大型风电机组模糊滑模鲁棒控制器设计与仿真［J］.中国电机工程学报，2008，28(14):136 －141.

［5］辜承林，韦忠朝，黄声华，等.对转子交流励磁电流实行矢量控制的变速恒频发机［J］.中国电机工程学报，2001，21(12):119－124.

［6］Sutton R S，Barto A G.Reinforcement Learning:an Introduction［M］.Cambridge:MIT Press，1998.

［7］张汝波.强化学习理论及应用［M］.哈尔滨:哈尔滨工程大学出版社，2001.

［8］余涛，周斌，甄卫国.强化学习理论在电力系统中的应用及展望［J］.电力系统保护与控制，2009，37(14):122 －128.

［9］Watkins J C H，Dayan Peter.Q － learning［J］.Machine Learning，1992(8):279－292.

［10］Tsitsiklis，John N.Asynchronous Stochastic Approximation and Q－ learning［J］.Machine Leaning，1994，16(3):185 －202.

［11］Richard S.Sutton，Andrew G.Barto.Reinforcement Learning:An In － troduction［M］.Cambridge:MIT Press，1988.

［12］余涛，胡细兵，刘靖.基于多步回溯Q(λ)学习算法的多目标最优潮流计算［J］.华南理工大学学报(自然科学版)，2010，38(10):139－145.

［13］刘其辉，贺益康，张建华.交流励磁变速恒频风力发电机的运行控制及建模仿真［J］.中国电机工程学报，2006，26(5):43－50.